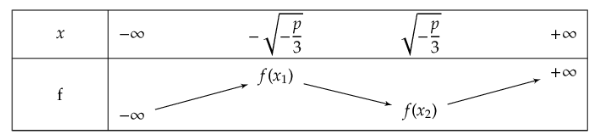Dans la cryptographie asymétrique, il y a une clé pour chiffrer dite clé publique et une clé pour déchiffrer dite clé secrète ou clé privée. Un exemple de cryptographie asymétrique très célèbre est le chiffrement RSA qui fut inventé par Rivest, Shamir et Adleman en 1977. Nous allons nous intéresser à une variante mathématiquement plus simple, le chiffrement de El Gamal, qui permet de bien comprendre le principe. Ce système est basé sur le fait que $(\mathbb{Z} /p\mathbb{Z})^*$ muni de la multiplication constitue un groupe commutatif. Nous verrons ensuite la cryptographie à l'aide de courbes elliptiques, qui est basée sur la même idée, mais le groupe sur lequel on travaille est alors plus abstrait.
Ce texte est fortement inspiré de la brochure « Cryptographie » de l'IREM d'Aquitaine,
Symétrique vs asymétrique
Pour définir la cryptographie asymétrique, le mieux est de commencer par ce qu'elle n'est pas, c'est-à-dire la cryptographie symétrique.
Un exemple très connu de cryptographie symétrique est le chiffrement par substitution, où l'on « mélange » l'alphabet par une permutation. Cette permutation est la clé qui permet de coder un texte, et c'est également elle qui permet de décoder le message une fois qu'il est chiffré. Le terme « symétrique » se réfère au fait que les deux intervenants qui communiquent entre eux (traditionnellement appelés Alice et Bob) jouent le même rôle, et ont la même connaissance de la clé, puisque c'est la même clé qui permet de chiffrer et de déchiffrer.
Le système par permutation n'est pas sûr (on peut le casser par analyse de fréquences) ; d'autres systèmes, tel celui utilisé par les Allemands pendant la 2ème guerre mondiale, qui s'appuyait sur la machine Enigma, sont nettement plus sûrs (quoique!) , mais également symétriques : la même machine, assortie de la clé (le réglage de départ de la machine), permettent de chiffrer et de déchiffrer.
De tels systèmes sont adaptés à des communications entre des personnes bien identifiées (deux chefs de guerre par exemple), qui doivent s’être mis d'accord à l'avance sur la clé. Elle n'est pas directement adaptée aux enjeux de la cryptographie moderne, où par exemple de très nombreux utilisateurs doivent envoyer de l'information de façon cryptée à une institution (par exemple une banque, un site web,...) sans s’être mis d'accord à l'avance avec cette institution.
Ces utilisations vont nécessiter la mise au point d'autres protocoles, plus praticables mais aussi en fait a priori plus sûrs !
Dans la cryptographie asymétrique, il y a donc une clé pour chiffrer dite clé publique et une clé pour déchiffrer dite clé secrète ou clé privée. La donnée de la clé publique seule ne permet pas de trouver la clé de déchiffrement.
Par exemple, dans le cadre du paiement en ligne, le vendeur fournit une clé publique : tout acheteur peut donc coder son numéro de carte bleue (l'acheteur ne se rend compte de rien, son ordinateur le fait pour lui à l’aide de cette clé publique) et c'est ce numéro chiffré qui est transmis par le réseau et est récupéré par le vendeur. Lui seul (ou plutôt son ordinateur) détient la clé privée permettant de déchiffrer. Ainsi tout le monde peut coder, mais une seule personne sait déchiffrer.
Un exemple de cryptographie asymétrique très célèbre est le chiffrement RSA qui fut inventé par Rivest, Shamir et Adleman en 1977. Il permet de coder des nombres entiers. (Pour coder un texte, il suffit de le traduire sous forme d'une suite d'entiers, ce qui n'est pas difficile.) Nous n'allons pas présenter ici ce système, mais nous intéresser à une variante mathématiquement plus simple, qui permet de bien comprendre le principe. Ce chiffrement a été introduit par ElGamal en 1984.
Méthode de chiffrement ElGamal
Description
On suppose que Alice souhaite transmettre un nombre entier à Bob.
Bob choisit un nombre premier $p$ (assez grand) et un nombre $d$ strictement plus petit que $p$, qui seront publics. Il choisit aussi un entier $s$ qui sera secret, et il calcule $h=d^s$ modulo $p$. La clé publique sera alors $(p, d, h)$ et la clé secrète $s$.
Si Alice souhaite envoyer un nombre $m$ inférieur à $p$ à Bob, elle commence par choisir un entier $a$, comme elle veut, puis elle calcule $r = m h^a$ modulo $p$, ainsi que $t = d^a$ modulo $p$.
Elle transmet alors ces deux nombres $(r,t)$ à Bob.
Puisque Bob connaît $s$, il peut alors calculer $t^s$. On verra (grace au théorème de Bézout rappelé plus bas) que Bob peut alors trouver un entier $u$ tel que $u. t^s$ est congru à 1 modulo $p$.
Bob calcule enfin le reste de la division euclidienne de $r u $ par $p$, et il obtient $m$.
En effet, par construction $t^s = d^{(sa)} = h^a$ modulo $p$. Donc toujours modulo $p$, on a $r u = m h^a u = m t^s u = m$. Ainsi, en calculant le reste de la division euclidienne de $r u $ par $p$, Bob retrouve $m$. C'est la commutativité de la multiplication dans $\mathbb{Z} /p\mathbb{Z}$ qui intervient.
Exemple
(Avec des petits nombres pour que ce soit lisible, évidemment pour que le système soit sûr les nombres doivent être beaucoup plus grands) :
Bob choisit $p = 23$, $d = 18$, $s = 3 $; alors $h = 13$.
Alice souhaite envoyer le nombre $m = 12$. Elle choisit $a = 5$.
Elle transmet alors $r = 2$ et $t = 3$.
Bob calcule alors $t^s = 27$. Il trouve par l'algorithme d'Euclide $1=-7\times 23 +6\times 27$ et il prend donc $ u=6$.
Le reste de la division euclidienne de $r u = 12$ par $p$ est alors 12 et Bob retrouve bien le message $m$.
Pourquoi c'est efficace : le problème du logarithme discret
Mettons nous à la place d'un espion. Il connaît (comme tout le monde), $(p, d, h)$. On suppose de plus qu'il a intercepté $(r, t)$. Il pourra décoder s'il retrouve $s$ (il lui suffira de faire comme Bob) ou s'il retrouve $a$ (en effet $r=mh^a$ modulo $p$, donc il lui suffira de multiplier $r$ par l'inverse de $h^a$).
Trouver $s$ revient à résoudre $h=d^s$ modulo $p$ lorsqu'on connaît $h,d$ et $p$. En d'autres termes il faut trouver "à quelle puissance élever $d$ pour trouver $h$ modulo $p$''. Avec l'exemple précédent, il s'agit de résoudre $18^s=13[23]$.
S'il n'y avait pas le modulo, donc si on travaillait dans $\mathbb{R}$ plutôt que dans $\mathbb{Z}/p\mathbb{Z}$, ce serait facile avec une calculatrice. On passerait au logarithme, et on aurait $s=\frac{\ln 13}{\ln 18}$. C'est pour cela que dans $\mathbb{Z}/p\mathbb{Z}$, on parle du problème du logarithme discret. Évidemment, quand $p$ est petit comme dans notre exemple, on peut faire une recherche exhaustive, mais avec des grands nombres, c'est une autre paire de manche. Le fait d'être dans $\mathbb{Z}/p\mathbb{Z}$ et pas dans $\mathbb{R}$ peut faire paraître les choses plus simples (on travaille sur un ensemble fini), mais en fait il n'en est rien.
Trouver $a$ revient également à résoudre un problème de logarithme discret.
Petits rappels d'arithmétique
Congruence
On dit qu'un entier $a$ est congru à un entier $b$ modulo l’entier $n$ si $n$ divise $a -b$.
Cela revient à dire que $a$ et $b$ donnent le même reste quand on les divise par $n$, de sorte que la différence est un multiple de $n$. On note cela $a \equiv b [n]$ ou encore $a \equiv b$ modulo $n$.
Propriétés.
La congruence est une relation d'équivalence. L’ensemble des classes modulo $n$ forme un groupe pour l’addition noté $\mathbb{Z} /n\mathbb{Z}$ .
De plus la multiplication des classes est possible : si $a \equiv b [n]$ et $c \equiv d [n]$ alors $ ac \equiv bd [n]$.
L’opération de multiplication obtenue est bien associative et commutative.
Par contre, par exemple dans $ \mathbb{Z} /6\mathbb{Z}$, on a $2\times 3\equiv 0[6]$ (on dit que l'anneau $\mathbb{Z} /6\mathbb{Z}$ n'est pas intègre) ; ainsi la classe de 2 modulo 6 n'a pas d'inverse dans $ \mathbb{Z}/6\mathbb{Z}$. (Cela vient du fait que 2 et 6 ne sont pas premiers entre eux.)
Égalité de Bézout
Soient $a$ et $b$ deux entiers relatifs. On note $d = PGCD (a,b)$. Alors il existe deux entiers relatifs $u$ et $v$ tels que $au + bv = d$.
On effectue l'algorithme d'Euclide1 pour trouver le PGCD $d$ de $a$ et $b$. Si $a>b$, on obtient ainsi une suite d'égalités $a = bq_1 + r_1$, $b = r_1q_2 + r_2$,..., $r_{n-2} = r_{n-1}q_n+ d$ (et $r_{n-1} = dr_n$).
On rappelle que le PGCD $d$ est le dernier reste non nul de cette suite de divisions : en effet on vérifie facilement que les diviseurs communs de $a$ et $b$ sont les diviseurs communs de $b$ et $r_1$, et en itérant sont aussi les diviseurs communs de $r_{n-1}$ et $d$, donc sont les diviseurs de $d$.
On obtient ainsi une égalité de Bézout entre $r_{n-2}$ et $r_{n-1}$ : $d = r_{n-2} - q_n r_{n-1}$ . On utilise alors l'avant-dernière égalité pour écrire $r_{n-1}$ en fonction de $r_{n-2}$ et $r_{n-3}$, ce qui donne alors une égalité de Bézout entre $r_{n-3}$ et $r_{n-2}$. Par une récurrence montante, on arrive bien ainsi à une égalité de Bézout entre $a$ et $b$.
L'algorithme d'Euclide étendu permet de systématiser cette méthode.
On trouve $27 = 23 + 4$, $23=4\times 5+3$, $4=3+1$. Le PGCD de 23 et 27 est donc bien 1, et on a :
$1=4-3 = 4-(23-4 \times 5) = -23+6\times 4 = -23+6\times (27-23) = 6\times 27 - 7\times 23$ comme utilisé plus haut.
Théorème de Bézout
Deux nombres entiers $a$ et $b$ sont premiers entre eux si et seulement si il existe deux nombres entiers $ u$ et $v$ tels que $au + bv = 1$.
D'après l'égalité de Bézout, si $a$ et $ b$ sont premiers entre eux il existe deux nombres entiers $u$ et $v$ tels que $au + bv = 1$. Réciproquement, on suppose qu'il existe deux nombres $u$ et $v$ tels que $au + bv = 1$.
Soit $d$ un diviseur de $ a$ et $b$, alors $d$ divise $au + bv$, donc $d$ divise $1$ : on en déduit $d = 1$.
Donc $a $ et $ b$ sont bien premiers entre eux.
Le théorème de Bézout (et l'algorithme d'Euclide présenté dans la preuve de l’égalité de Bézout) permettent de savoir si un élément de $\mathbb{Z} /n\mathbb{Z}$ est inversible et de trouver son inverse.
Corollaire du théorème de Bézout
Dans $(\mathbb{Z} /n\mathbb{Z}, +, \times)$, la classe d'un entier $m$ est inversible si et seulement si $m$ et $n$ sont premiers entre eux.
La classe de $m$ est inversible dans $\mathbb{Z} /n\mathbb{Z}$ si et seulement si il existe un entier $u$ telle que $mu\equiv 1[n]$. Ainsi la classe de $m$ est inversible dans $\mathbb{Z} /n\mathbb{Z}$ si et seulement si il existe un entier $u$ et un entier $v$ tels que $mu-nv = 1$. On applique alors le théorème de Bézout et on conclut bien que la classe de $m$ est inversible dans $\mathbb{Z} /n\mathbb{Z}$ si et seulement si $m$ et $n$ sont premiers entre eux.
Corollaire du corollaire...
$(\mathbb{Z} /n\mathbb{Z}, +, \times)$ est un corps si et seulement si $n$ est premier.
Si $n$ est premier, une classe non nulle de $(\mathbb{Z} /n\mathbb{Z}, +, \times)$ est la classe d'un entier $m$ non divisible par $n$, donc premier avec $n$, et donc inversible. Réciproquement, si $n$ n'est pas premier, il s’écrit $n=pq$ avec $p$ et $q$ entiers différents de $n$. Donc la classe de $p$ modulo $n$ ne peut pas être inversible.
Interlude sur l'exponentiation rapide
Pour chiffrer et déchiffrer dans ce système, on se retrouve à devoir calculer des expressions du type $x^y [N]$ où $y$ peut être assez grand. Or si on calcule d'abord $x^y$ puis que l'on fait la division euclidienne par $N$, il est fort possible qu'on dépasse la capacité d'un ordinateur, et ce n'est en fait pas nécessaire.
Il est plus judicieux d'utiliser le fait que si $x_1 \equiv a [N]$ et si $x_2 \equiv b [N] $ alors $x_1x_2 \equiv ab [N]$ pour se ramener toujours à des nombres inférieurs à $N$.
$5^{100}$ est un nombre gigantesque.
Mais $5^2 = 25 = 7[18]$.
Donc $5^4 = (5^2)^2 = 49 [18]$, et finalement $5^4 = 13 [18]$.
De même $5^8 = 13^2 [18]$ donc $5^8 = 7 [18]$.
$5^{16} = 13 [18]$.
$5^{32} = 7 [18]$.
et enfin $5^{64} =13 [18]$.
Finalement $5^{100} = 5^{(64+32+4)} = 13\times 7\times 13 [18]$, donc $5^{100} = 13 [18].$
Le principe de manière générale est d'écrire l'exposant $y$ en base 2 (dans l'exemple ci-dessus 100 = 64 + 32 + 4) et de calculer les puissances 2, 4, etc , en élevant au carré à chaque fois et en calculant le reste de la division euclidienne par $N$ à chaque étape. Les nombres qu'on manipule ainsi restent petits.
Principes de la cryptographie asymétrique
Le principe à la base de tout système de cryptographie asymétrique est la notion de fonction à sens unique. On entend par cela une fonction facile à calculer mais
difficile à inverser, au sens où on ne dispose pas d'algorithme permettant le calcul de l'antécédent d'un nombre en un temps raisonnable.
Ainsi pour ElGamal : le calcul à une certaine puissance modulo un entier $n$ est facile mais pour décoder ElGamal (sans connaître la clé secrète $s$ ni $a$) il faut comme on l'a vu résoudre le problème du logarithme discret (trouver $a$ si on connaît $d$ et $d^a$ modulo $p$). Dans le système RSA il faut trouver $p$ et $q$ tels que $n = pq$, ce qui est très long, même pour un ordinateur puissant, si $n$ est très grand. Cela explique que de gros moyens en cryptographie sont mis sur la recherche d’algorithmes de factorisation les plus rapides possibles.
Pour concevoir d'autres systèmes, on peut chercher d'autres fonctions difficiles à inverser dans le cadre de l'arithmétique dans $\mathbb{Z} /n\mathbb{Z}$. Il est à noter qu'on ne sait en général pas prouver qu'une fonction est difficile à inverser : ce n'est pas parce que l'on ne connaît pas d'algorithme efficace qu'il n'en existe pas.
On peut aussi changer l'espace sur lequel on travaille, en gardant le même genre de fonctions. Ainsi, le système cryptographique très simple ElGamal est basé sur le fait que $(\mathbb{Z} /p\mathbb{Z})^*$ muni de la multiplication constitue un groupe commutatif. La cryptographie à l'aide de courbes elliptiques est basée sur la même idée, mais le groupe sur lequel on travaille est alors plus abstrait.
Utilisation des courbes elliptiques
On va travailler sur des objets plus sophistiqués que les entiers : ce seront des points sur des courbes appelées courbes elliptiques. Cela va donner une méthode de cryptographie plus sûre encore que RSA. Les messages qu'on pourra transmettre par ce système seront alors des points sur ces courbes. Les courbes elliptiques utilisées en cryptographie sont des sous-ensembles de $(\mathbb{Z}/p\mathbb{Z})^2$, mais pour se représenter mieux les choses on va commencer par travailler dans $\mathbb{R}^2$.
Définition et représentation des courbes elliptiques dans $\mathbb{R}^2$
Une courbe elliptique (affine) est l'ensemble des points de coordonnées réelles $(x , y)$ où $x$ et $y$ vérifient :
$$y^2 = x^3+ ax + b\,\,\mbox{ avec } 4a^3 + 27b^2\neq 0 $$
Comme leur nom l’indique, il y a un lien entre les courbes elliptiques et l’ellipse. On obtient une représentation paramétrique des courbes elliptiques avec des fonctions elliptiques, elles-mêmes liées aux intégrales elliptiques qui servent à calculer la longueur de l’ellipse. Weierstrass (1815-1897) a exhibé les courbes elliptiques en poursuivant les travaux menés par Abel (1802-1829) sur les intégrales elliptiques. Mais une courbe elliptique n'est pas une ellipse, dont l'équation ne contient pas de terme $x^3$.
Une courbe elliptique est bien évidemment toujours symétrique par rapport à l'axe des abscisses.
Les solutions de l’équation $x^3 + ax + b = 0$ sont les abscisses des points d’intersection de cette courbe avec l’axe des abscisses.
$\Delta = 4a^3 + 27b^2$ est le discriminant de l’équation du troisième degré $x^3+ ax + b = 0.$
Si $\Delta = 0$, le polynôme $x^3 + ax + b$ possède trois racines réelles (avec multiplicité), non toutes distinctes. S’il n’est pas nul il n’y pas de racine multiple. Cette condition garantit que la courbe elliptique dans $\mathbb{R}^2$ est lisse (elle n'a pas de point de rebroussement).
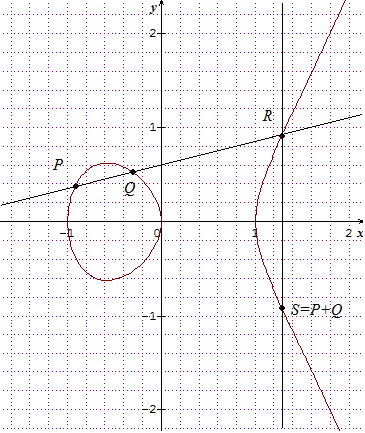
Une courbe elliptique 1 ($\Delta \neq 0$) a l'une des deux allures suivantes (la définition de la somme et la construction du point S = P + Q sont introduites dans la suite du texte.)
- si $\Delta<0$, le polynôme $x^3+ax+b$ a alors trois racines réelles distinctes, donc la courbe possède trois intersections avec l'axe des abscisses.
- Si $\Delta > 0$, le polynôme a alors une unique racine réelle.
La représentation graphique d'une courbe elliptique peut se faire en terminale, par exemple pour les courbes d’équation $y^2 = x^3-x \, (C1)$ et $ y^2 = x^3-x+1 \, (C2)$, en commençant par l'étude du signe du polynôme.
Les élèves peuvent étudier les variations et tracer la courbe représentative des fonctions $f_1$ et $f_2$ définies par $f_1(x) = \sqrt{x^3-x}$ et $f_2 (x) =\sqrt{x^3-x+1}$.
On obtient les deux courbes complètes par une symétrie par rapport à l’axe des abscisses. On peut faire remarquer alors que ces courbes ne sont plus la représentation graphique de fonctions.
On trouvera en annexe une étude mathématique détaillée qui permet de comprendre à quoi ressemblent les courbes elliptiques à l’aide d’étude de fonctions. Ce travail peut être mené en terminale.
On rajoute par convention à cette courbe elliptique un « point à l'infini » qu’on notera ici $P_0$ (il faut imaginer qu'il correspond à une ordonnée $y$ infinie).
Comment additionner des points
On définit alors une loi de groupe notée + sur cet ensemble de points, de la façon suivante :
Cas général. Soient $P$ et $Q$ deux points sur la courbe. On trace la droite $(PQ)$. Elle intersecte la courbe en un troisième point $R$. On note alors $S$ le symétrique de $R$ par rapport à l'axe des abscisses, et on définit $P+Q = S$.
Cas particuliers :
$\bullet$ Si $P = Q$, on prend pour droite $(PQ)$ la tangente à la courbe en $P$. On notera $P + P=2\cdot P$
$\bullet$ $P+P_0 = P$ ($P_0$ est l'élément neutre)
$\bullet$ Si $P$ et $Q$ sont symétriques par rapport à $(Ox)$, c'est-à-dire $P(x,y)$ et $Q(x,-y)$, la droite $(PQ)$ intersecte la courbe « à l'infini » : on définit alors $P + Q=P_0$. $P$ et $Q$ sont opposés. On note $P=-Q$.
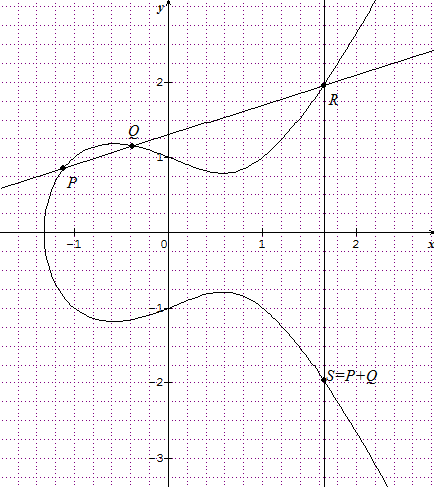
Pour montrer que c'est une loi de groupe, il faudrait démontrer qu'elle est associative, ce qui est bien le cas mais n'est pas évident du tout. On peut simplement le constater sur l’exemple suivant avec $y^2 = x^3-x+\frac{1}{4}$.
On choisit un point $P$ sur la courbe : ici on a pris $P (0 ; 1)$. On trace la tangente à la courbe en $P$ pour obtenir $-2 \cdot P$ puis son symétrique $ 2\cdot P$. On construit ensuite $3\cdot P = 2 \cdot P + P$ ; $4\cdot P$ n’est pas visible sur le dessin donc pour $5\cdot P$ on peut utiliser $ 5\cdot P = (2\cdot P + 3\cdot P)$ ; en joignant $(-2\cdot P)$ et $(-3\cdot P)$ on peut aussi directement obtenir $(-(-5\cdot P))$. On continue ainsi pour $6\cdot P = 5\cdot P + P$ mais il sort de la figure ;
$7\cdot P = 5\cdot P + 2\cdot P$ et $8\cdot P = 7\cdot P + P$. Ici, on peut vérifier l’associativité de l’addition : $5\cdot P + 3\cdot P = 8\cdot P$.
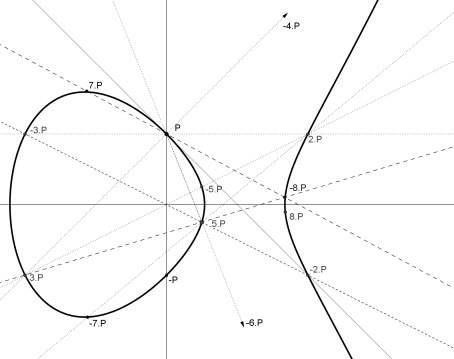
Il existe des formules explicites pour trouver les coordonnées de $P + Q$ en fonction des coordonnées de $P$ et de $Q$1. On peut les utiliser pour montrer en particulier que lorsque les coefficients de la courbe elliptique sont des entiers et en choisissant un point $P$ de coordonnées rationnelles, tous les multiples $n\cdot P$ auront aussi des coordonnées rationnelles mais cela dépasse largement le cadre de ce texte.
Un système cryptographique avec des courbes elliptiques
On peut maintenant concevoir un système cryptographique analogue au système ElGamal.
On choisit un entier $q$ premier (dans la pratique, on le choisit très grand). Au lieu de travailler dans le corps des réels, on travaillera dans le corps $\mathbb{Z} /q\mathbb{Z}$. On choisit ensuite deux entiers $a$ et $b$ inférieurs à $q$ tels que $4a^3 + 27b^2\neq 0 $ modulo $q$. On considère alors l’ensemble des points dont les coordonnées $(x ;y)$ dans $\mathbb{Z} /q\mathbb{Z}$ vérifient $y^2 = x^3+ ax + b$. On continuera de l’appeler « courbe elliptique »2. On définit la même opération sur ces points en utilisant les formules explicites mentionnées dans le paragraphe précédent et on obtient aussi un groupe.
Grâce à ces formules, un ordinateur peut « facilement» calculer le point $(P + P +...+ P) = n\cdot P$ lorsqu'on lui donne l'entier $n$ et le point $P$ (et ce de façon exacte).
Le calcul « difficile » consiste à calculer $n$ lorsqu'on connaît les points $n\cdot P$ et $P$.
Pour obtenir ces deux dernières propriétés, qui permettent d’avoir un système cryptographique sûr, il était nécessaire de se placer dans $\mathbb{Z} /q\mathbb{Z}$.
Dans ce système cryptographique :
- la clé publique de Bob est le triplet (une courbe elliptique, un point $P$ sur la courbe, le point $Q = n\cdot P$),
- sa clé privée est l'entier $n$.
Pour comprendre le principe, on peut faire fonctionner un exemple en utilisant en fait à nouveau la courbe elliptique à coordonnées réelles.
On suppose que le message qu'Alice souhaite envoyer est un point $M$ sur la courbe 3. Alice choisit alors un entier $k > 1$, calcule le point $k\cdot P$ et transmet à Bob les deux points $(k\cdot P, M+k\cdot Q)$.
Bob connaît $n$ : il peut donc déterminer $n\cdot k \cdot P = k\cdot Q$. Il peut alors calculer $-k\cdot Q$, et finalement il trouve $(M+k\cdot Q ) + (-k\cdot Q) = M$.
Remarque : Alice doit garder $k$ secret : si un espion connaît $k$, il peut retrouver $M$. Mais comme Bob connaît $n$, il n'a pas besoin de $k$.
Exemple : avec $n = 3$ et $k = 2$. (Pour que le système soit sûr $n$ et $k$ doivent être beaucoup plus grands)
Alice récupère la clé publique et connaît donc les points $P$ et $ Q $
Elle détermine alors les points $U = 2\cdot P$ et $V = M + 2\cdot Q $, et transmet à Bob le couple $(U, V)$.
Bob calcule alors $3 \cdot U$ , puis $V-3\cdot U$. Or $Q = 3\cdot P$ donc $3\cdot U = 3\cdot 2\cdot P = 2\cdot 3\cdot P = 2\cdot Q$
Finalement Bob a calculé $V-3\cdot U = (M + 2\cdot Q)-2\cdot Q = M$
Remarque : on note traditionnellement cette loi de groupe sur les points par un signe d'addition. Dans le système ElGamal présenté plus haut, la loi de groupe utilisée est la multiplication. C'est pourquoi on ne voit pas forcément à première vue que le principe est fondamentalement le même. Mais c'est bien le cas !
Il y a encore beaucoup de questions ouvertes concernant les courbes elliptiques, et de nombreux chercheurs s'y attaquent : en particulier on ne sait pas en général combien une telle courbe comporte de points... Le fait que les calculs sur ces objets soient mathématiquement plus sophistiques fait que, en pratique, les algorithmes de cryptographie utilisant les courbes elliptiques prennent plus de temps et de ressources que, par exemple, l'algorithme RSA. Ils sont donc plutôt utilisés pour s'échanger une clé, qui peut ensuite utilisée avec un protocole de cryptographie symétrique.
Annexe : Étude de l'allure de ces courbes.
On va ici décrire l’ensemble des points de coordonnées réelles $(x,y)$ où $x$ et $y$ vérifient $y^2 = x^3 + px +q$.
On va voir que l’allure des courbes dépend du signe du discriminant $4p^3 + 27q^2$, et en particulier, comme mentionné plus haut, que si $4p^3 + 27q^2 \neq 0$, la courbe admet bien une tangente en chaque point.
Une telle courbe est un cas particulier d'une cubique, courbe dans le plan dont l’équation générale est de la forme
$Ax^3+ By^3+ Cx^2y + Dxy^2 + Ex^2 +Fy^2 + Gxy + Hx + Iy + J = 0$
avec au moins un des quatre paramètres $A, B, C$ ou $D$ non nuls. Elles peuvent ou non être la représentation graphique d'une fonction : ainsi la courbe d’équation $y = x^3$ est la représentation graphique d’une fonction, et sa description est simple. Mais la courbe d’équation $y^2 = x^3 + 1$ est aussi une cubique qui n’est pas la représentation graphique d’une fonction (il y a des points sur cette courbe de même abscisse $x$ et d'ordonnée différente).
Pour étudier une telle courbe on peut commencer par remarquer que si $(x,y)$ appartient à cette courbe, $(x,-y)$ également : elle est donc symétrique par rapport à l'axe des abscisses. On peut donc se restreindre à l’étude des courbes d’équation $y =\sqrt{ x^3 + px +q}$. Pour cela on doit naturellement commencer par étudier les fonctions qui à $x$ associent $x^3 + px +q$ : d'une part on a besoin de connaître leur signe pour savoir quand la racine est définie; de plus le fait qu'on compose avec la fonction racine carrée, croissante, fait qu'il y a un lien dans la forme entre les courbes d’équation $y = x^3 + px +q$ et celles d’équation $y =\sqrt{x^3 + px +q} $.
Quelques remarques sur la résolution de l’équation du 3ème degré et les fonctions polynômes de 3ème degré.
Forme réduite pour résoudre l’équation $x^3 + ax^2 + bx + c = 0$ et pour représenter la courbe de la fonction $f$ définie par $f(x) = x^3 + ax^2 + bx + c$
Nous prenons le coefficient du terme en $x^3$ égal à 1 car même si ce n’est pas le cas c’est un nombre non nul. Nous pouvons donc supposer que nous avons divisé les deux membres de l’équation par ce nombre. Pour la fonction, ceci revient à transformer la courbe représentative par une affinité (multiplication des ordonnées) comme lorsqu’on remplace la parabole d’équation $y= ax^2$ par celle d’équation $y = x^2$.
Par un changement d’inconnue pour l’équation ou une translation des axes pour la courbe, on peut ensuite éliminer le terme en $x^2$.
On pose $x = X + u$ et l’équation devient :
$(X + u )^3 + a (X + u )^2 + b (X + u ) + c = 0$
Ou encore $X^3 + X^2 (3u+a) + X (3 u^2 + 2au+ b) + u^3 + au^2 + bu+ c = 0$
Pour éliminer le coefficient de $X^2$ il suffit de choisir $u = -\frac{a}{3}$.
L’équation est alors de la forme $X^3 + pX + q = 0 $ et il suffit donc d’étudier les fonctions $f$ définies pour tout réel $x$ par $f(x) = x^3 + px + q$.
Nombre de racines réelles de l’équation $x^3 + px + q = 0$ et variations de la fonction $x\mapsto x^3+px+q$
On rappelle, mais on ne l'utilisera pas ici, qu'il existe un procédé de résolution des équations de degré 3, avec la formule de Cardan (Ars Magna-1545) découverte par Del Ferro, redécouverte par Tartaglia (vers 1530). Bombelli a travaillé à partir de ces formules (en 1572), ce qui a motivé l’introduction de l’écriture de nombre sous la forme $a + b\sqrt{-1}$ . (La notation $\sqrt{-1}= i$ a été introduite par Euler en 1777.)
L’étude de la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = x^3 + px + q$ va nous donner les résultats dont nous avons besoin.
On a : $f ’(x) = 3 x^2 + p$
- 1er cas : $p\geq 0$ : la dérivée est positive donc la fonction $f$ croit de façon monotone sur $\mathbb{R}$. Elle s’annule une seule fois et donc le polynôme a une seule racine réelle.
- 2ème cas : $p<0$ : la dérivée change deux fois de signe pour $x_1 = -\sqrt{-\frac{p}{3}}$ et $x_2 =\sqrt{-\frac{p}{3}} $ce qui donne le tableau de variations suivant :
- Si $f(x_1)$ et $f(x_2)$ sont de signe contraire, c'est-à-dire $f(x_1) f(x_2) < 0$, la fonction s’annule trois fois, donc l’équation a trois racines réelles.
- Si $f(x_1)$ et $f(x_2)$ sont de même signe (positif ou négatif), c'est-à-dire $f(x_1) f(x_2) > 0$, la fonction s’annule une seule fois, donc l’équation a une seule racine réelle.
- Si $f(x_1) f(x_2) = 0$, ceci veut dire que $f(x_1)$ ou $f(x_2)$ est nul, donc $x_1$ ou $x_2$ est racine double de l’équation et la courbe est tangente à l’axe des abscisses en ce point.
Dans tous les cas, $f''(x) = 6x$. La courbe a donc un point d’inflexion pour $x = 0$. La concavité de la courbe est tournée vers le bas sur $]-\infty , 0]$ et elle est tournée vers le haut sur $[0, +\infty[$.
On peut calculer $f(x_1) f(x_2)$ en fonction de $p$ et $q$ :
\begin{eqnarray*}
f(x_1)f(x_2)&=\left[(\sqrt{-\frac{p}{3}})^3 + p\sqrt{-\frac{p}{3}} + q\right]\left[-(\sqrt{-\frac{p}{3}})^3 -p\sqrt{-\frac{p}{3}} + q\right]\\
&=\left(-\frac{p}{3} \sqrt{-\frac{p}{3}} + p \sqrt{-\frac{p}{3}} + q\right)
\left(\frac{p}{3} \sqrt{-\frac{p}{3}} -p \sqrt{-\frac{p}{3}} + q\right)\\
&= \left(q+ 2\frac{p}{3} \sqrt{-\frac{p}{3}}\right) \left(q- 2\frac{p}{3} \sqrt{-\frac{p}{3}}\right) = \frac{4p^3+27q^2}{27}
\end{eqnarray*}
Dans le cas $p<0$, il y a donc trois racines réelles distinctes si et seulement si $f(x_1)f(x_2)<0$, i.e. $4p^3 + 27 q^2 < 0$.
Rappelons que dans le cas où $p\geq 0$, on a $4p^3 + 27 q^2 \geq 0$ et, comme nous l’avons vu, une seule racine réelle.
En résumé : $4p^3 + 27 q^2 <0$ est donc bien la condition nécessaire et suffisante pour avoir trois racines réelles distinctes.
Exemples de courbe d’équation $y = x^3 + px + q$
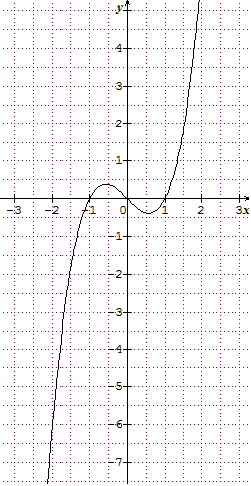
$y = x^3-x = x(x^2-1) $
On considère la fonction $f:x\mapsto x^3-x$.
L’équation $f(x) = 0$ a trois racines réelles évidentes : 0 ; 1 et –1.
On a bien $4p^3 + 27 q^2 = - 4$ négatif.
$f’(x) = 3 x^2-1$ : on a donc deux changements de signe de la dérivée.
$f''(x)=6x$ : on a donc un point d’inflexion à l’origine.
La fonction est impaire donc la courbe est symétrique par rapport à l’origine.
On peut vérifier que le produit $f(x_1) f(x_2)$ est bien égal à $\frac{4p^3+27q^2}{27} = \frac{-4}{27}$.
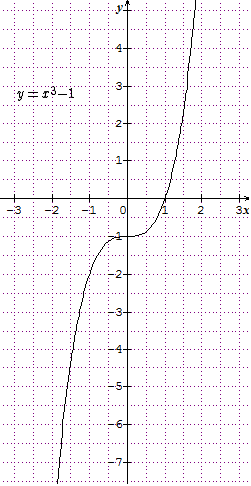
$y = x^3-1 = (x-1) (x^2 + x + 1) $
On considère la fonction qui à tout réel $x$ associe $f(x) = x^3-1$;
l’équation $f(x) = 0$ a une seule racine réelle, 1.
On a bien $4p^3 + 27 q^2$ positif.
$f’$ est toujours positive ou nulle, la fonction est donc croissante.
$f''$ s’annule en 0 en changeant de signe, on a donc un point d’inflexion au point (0,-1). En ce point la tangente est horizontale.
De plus ce point est centre de symétrie pour la courbe car $f(x) + 1 = x^3$ change de signe si $x$ change de signe.
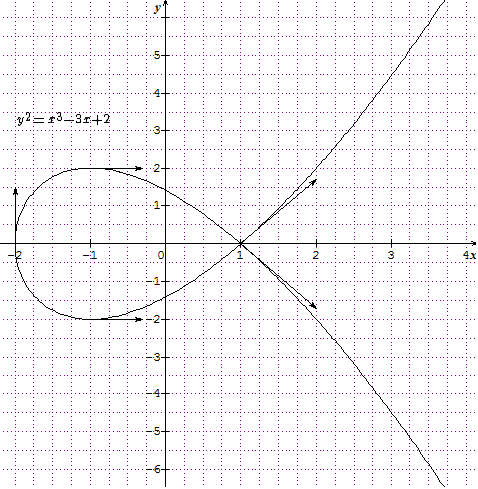
$y = x^3-3x + 2 = (x-1)^2 (x + 2)$
On considère la fonction qui à tout réel $x$ associe $f(x) = x^3-3x + 2$.
L’équation $f(x) = 0$ a une racine réelle simple (-2) et 1 est une racine réelle double.
On a bien $4p^3 + 27 q^2 = 0$.
$f’(x) = 3 x^2 -3 = 3(x + 1)(x-1)$ change deux fois de signe.
Au point d’abscisse 1, la courbe est tangente à l’axe des abscisses (racine double).
$f''(x) = 6x$ : on a donc un point d’inflexion au point (0 ; 2). De plus, ce point est centre de symétrie pour la courbe car $f(x) + 2 = x^3-3x$ change de signe si $x$ change de signe.
Courbes d’équation $y^2 = x^3 + px +q$
Ces courbes se situent dans des domaines où $x^3 + px +q$ est positif ou nul. On pourra les décomposer en deux branches
$y =\sqrt{x^3 + px +q}$ et $y = -\sqrt{x^3 + px +q}$.
Ces branches sont symétriques par rapport à l’axe des abscisses.
Courbe d’équation $y^2 = x^3-x$
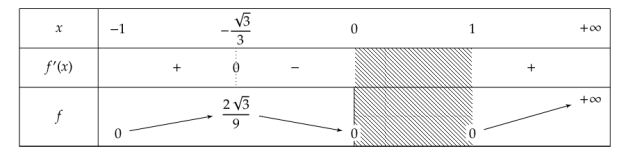
On commence par tracer la courbe représentant la fonction $f: x\mapsto \sqrt{x^3-x}$.
Domaine de définition : $[-1, 0] \cup [1,+\infty[$.
$\forall x \in ]-1,0[\cup]1,+\infty[$, $f’ (x) =\frac{3x^2-1}{2\sqrt{x^3-x}}$. $f'$ change une fois de signe dans le domaine de définition.
On remarque que la tangente à la courbe sera verticale pour $x = -1, x = 0$ et $x = 1$.
On peut dresser le tableau de variations :
Après symétrie par rapport à l’axe des abscisses on obtient la courbe complète, du type de celles utilisées en cryptologie. Le fait que les tangentes soient verticales pour $x = -1, x = 0$ et $x = 1$ entraîne qu'on a bien une tangente verticale également en ces points pour la courbe complète, et pas 2 demi-tangentes.
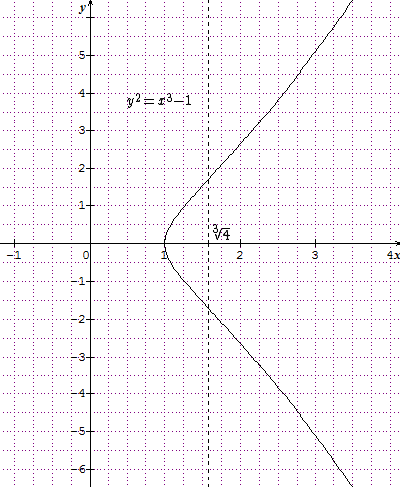
Courbe d’équation $y^2 = x^3- 1$
On commence par tracer la courbe représentant la fonction $x\mapsto f(x) =\sqrt{x^3- 1}$.
Domaine de définition : $[1,+\infty[$.
$\forall x>1, f’ (x) = \frac{3x^2}{2\sqrt{x^3-1}}$. La dérivée est toujours positive dans le domaine de définition.
Au point d’abscisse $x = 1$, la tangente est verticale.
On trouve $\forall x>1, f''(x) = \frac{3x(x^3-4)}{4(x^3-1)\sqrt{x^3-1}}$. Il y a donc un point d’inflexion d’abscisse $\sqrt[3]{4}$.
$f''(x) <0$ si $x < \sqrt[3]{4}$ (concavité vers le bas),
$f''(x) >0$ si $x >\sqrt[3]{4} $ (concavité vers le haut).
En complétant par la symétrie par rapport à l’axe des abscisses on obtient la courbe complète. Là encore, la tangente verticale en $x-1$ donne bien lieu à une tangente verticale après symétrie pour la courbe complète.
Courbe d’équation $y^2 = x^3-3x + 2 = (x-1)^2(x + 2)$
On commence par tracer la courbe représentant la fonction $x\mapsto f(x) =\sqrt{x^3-3x + 2}$.
Domaine de définition : $[- 2, +\infty[$, domaine de dérivabilité $]-2,1[\cup ]1,+\infty[$.
$\forall x \in ]-2,1[\cup ]1,+\infty[, f’ (x) =\frac{3x^2-3}{2\sqrt{x^3-3x+2}}$. $f'$ change deux fois de signe dans le domaine de définition.
La tangente est horizontale au point de coordonnées $(-1, 2)$.
La tangente est verticale au point de coordonnées $(-2, 0)$.
On peut chercher étudier ce qui se passe au point de coordonnées (1, 0).
Si $x$ tend vers 1 par valeurs supérieures on a :
$\lim_{x\rightarrow 1^+} f’ (x) = \lim_{x\rightarrow 1^+} \frac{3(x-1)(x+1)}{2(x-1)\sqrt{x+2}} = \sqrt{3}$.
Si $x$ tend vers 1 par valeurs inférieures :
$\lim_{x\rightarrow 1^-} f’ (x) = \lim_{x\rightarrow 1^-} \frac{3(x-1)(x+1)}{-2(x-1)\sqrt{x+2}} = -\sqrt{3}$
La fonction n'est donc pas dérivable en 1, il y a deux demi-tangentes au point $(1,0)$ : il s'agit d'un point anguleux (nous sommes dans le cas $4p^3 + 27 q^2 = 0$). Après symétrie, ces deux demi-tangentes donneront lieu à deux tangentes pour la courbe complète : on aura un point double.
On peut dresser le tableau de variations :
Finalement, on obtient la courbe ci-contre :
Remarques sur la forme des courbes
Dans le troisième exemple, la racine double $x = 1$ de la courbe d’équation $y = x^3 -3x + 2$ induit un point double pour la courbe d’équation $y^2 = x^3-3x + 2$.
On ne se servira pas d'une telle courbe en cryptologie. En effet le codage consiste à calculer pour les points $P$, la somme $P + P + …. + P = n\cdot P$. Pour cela on utilise la tangente à la courbe. En $P(1 ; 0)$, il y a deux tangentes, la somme $P + P$ n’est pas définie.
Références
[1] Brochure de l'IREM d'Aquitaine "Cryptographie"
[2] Page Wikipedia sur le cryptosystème ElGamal
[3] Sur le site Bibmath : Les courbes elliptiques
[4] Sur Culturemath : Ghazal Kachigar, La cryptographie et les ordinateurs quantiques