Les découpages géométriques passionnent professionnels et amateurs. La gageure consiste à transformer, avec le nombre minimal de coups de ciseaux et en réarrangeant les morceaux, une forme en une autre.

Le grand classique du découpage est l'ouvrage de Harry Lindgren Recreational Problems in Geometric Dissections and How to Solve Them, paru en 1964, puis complété et republié en 1972. En dehors de sa passion pour la géométrie et son métier d'agent de brevets, Harry Lindgren fut jusqu'à sa mort, en 1992, l'ardent défen­seur d'une réforme radicale de l'orthographe anglaise qu'il souhaitait fondée sur un système phonétique rigoureux. Que n'a-t-il fait école !

Depuis 1972, de nombreux ajouts ayant fait progresser l'art popu­laire des dissections, une nouvelle synthèse s'imposait. Le livre de Greg Frederickson paru en 1997 sous le titre Dissection : Plane and Fancy vint combler ce manque. Sa réalisation est d'une remarquable qualité, tant sur le plan des informations que l'auteur est allé rechercher patiemment dans toutes sortes de publications, pour la plupart inaccessibles, que pour les belles illustrations qui nous font découvrir à chaque page des constructions astucieuses et élégantes. Ce livre prouve que l'ingéniosité des amateurs de récréations mathématiques engendre des merveilles esthétiques et d'authentiques énigmes diffi­ciles.

Le découpage du croissant de lune en croix grecque et en carré (voir la figure 1) est un classique du genre perfectionné par les deux frères rivaux du découpage, Sam Lloyd (1841-1911) et Henry Dudeney (1857-1930).

Le dessin (a) donne une solution en sept pièces de la transformation du croissant en croix grecque. Le croissant de lune utilisé possède une hauteur égale à cinq fois la largeur. La construction résulte d'une correction apportée par G. Frederickson à une solution inexacte proposée par Sam Lloyd. Le croissant de lune auquel s'intéressa H. Dudeney est légèrement différent : sa hauteur est égale à quatre fois sa largeur. Le dessin (b) montre un découpage en huit pièces du croissant de Lloyd conduisant au carré.

Assez étrangement, les résultats généraux de M. Laczkovich, S. Banach et A. Tarski sur les découpages ensemblistes utilisant l'axiome du choix ne sont pas mention­nés dans le livre de G. Frederickson, qui n'a voulu retenir que les découpages effectifs.

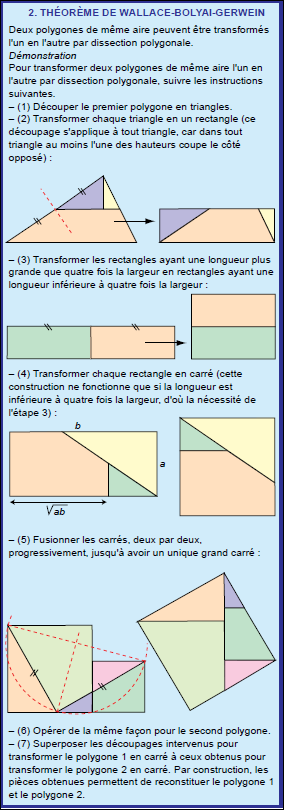
Il est évident que, si en découpant un polygone A en un nombre fini de morceaux polygonaux et en les recombinant, on reconstitue un polygone B, alors les polygones A et B ont des aires égales. Moins évidente est la propriété réciproque : si deux polygones A et B ont des aires égales, alors on peut toujours découper le premier en un nombre fini de polygones qui se recombineront pour former le second.

C'est le théorème de Lowry-Wallace-Bolyai-Gerwein (démontré indépendamment plusieurs fois au XIXe siècle) : deux polygones sont décompo­sables par dissection polygonale, si et seulement si, ils ont la même aire (voir la figure 2).

La démonstration générale donne des découpages comprenant un trop grand nombre de pièces, aussi en cherche-t-on d'autres plus économiques. C'est la source d'une multitude de casse-tête géométriques : les records sont régulièrement battus, parfois au grand dam des spécialistes qui pensaient impossible d'améliorer leur solution !

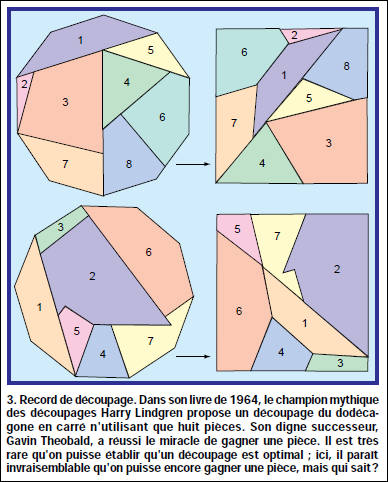
Tel est le cas de la transformation proposée par Lindgren du décagone en carré, qui était déjà miraculeusement réalisée avec huit pièces seulement et que l'amateur anglais Gavin Theobald améliora en un découpage de sept pièces (voir la figure 3).

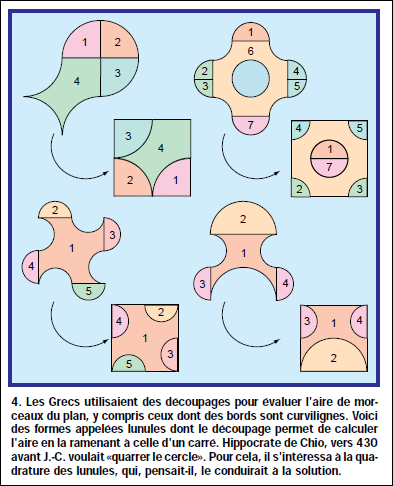
Lorsque l'on considère non plus des polygones mais des figures à bords curvilignes, par exemple des arcs de cercles (voir la figure 4), le théorème de Lowry-Wallace-Bolyai-Gerwein n'assure plus qu'un découpage existe.

Pourtant l'idée des « découpages-recompositions » était une des méthodes utilisées par les Grecs pour « quarrer » des surfaces à bords curvilignes. « Quarrer » une aire signifie la calculer en ramenant la figure initiale à celle d'un carré. Ces figures aux bords curvilignes qu'on peut quarrer étaient appelées des lunules, et les Grecs savaient que certains découpages étaient difficiles, voire impossibles.

Deux quadratures du cercle

Le fameux problème de la quadrature du cercle est attribué à Anaxagore1. Alors qu'il était emprisonné pour avoir soutenu que la Lune ne faisait que refléter la lumière du Soleil, il se serait posé, il y a vingt-cinq siècles, la question de mettre en relation un cercle et un carré de même aire.

On peut interpréter l'expression quadrature du cercle de deux façons différentes.

La première, que nous appellerons « le problème classique de la quadrature du cercle », se formule ainsi : est-il possible, en n'utilisant que la règle et le compas, de tracer un carré de la même aire qu'un cercle donné ?

Résoudre le problème équivaut à tracer à la règle et au compas un segment de longueur $\pi$ à partir de la donnée d'un segment de longueur 1, ce qui ne serait possible que si $\pi$ était exprimable par radicaux carrés (comme $\sqrt{2+\sqrt{5}/(1+\sqrt{17})}$)2. Cela impliquerait que $\pi$ est solution d'une équation polynomiale à coefficients entiers, ce qui n'est pas le cas, puisque $\pi$ est un nombre transcendant, comme Ferdinand von Lindemann l'a prouvé en 1882 !

La seconde interprétation, que nous dénommerons « problème de la quadratme du cercle par découpages », est la suivante : est-il possible de découper un cercle (on devrait dire un disque) en un nombre fini de morceaux — auxquels on n'impose pas d'être traçables à la règle et au compas — de façon qu'en recombinant les morceaux on obtienne un carré de même aire ? Recombiner signifie déplacer les morceaux sans les déformer, en leur appliquant uniquement des translations, des rotations ou des symétries.

Ce problème, posé par le logicien polonais Alfred Tarski en 1952, sera résolu plus vite que son ancêtre classique. Sa solution complète est à la fois étonnante et décevante. Elle comporte deux volets.

Avec des ciseaux ou avec des ensembles ?

Si l'on impose aux morceaux du découpage d'être des formes géométriques limitées par des arcs de courbes régulières (cas du découpage aux ciseaux), alors L. Dubins, M. Hirsch et J. Karush ont établi en 1963 que la réponse est négative : la quadrature du cercle par découpage aux ciseaux est impos­sible. Il découle de leur théorème que vous ne pourrez donc pas décom­poser aux ciseaux un cercle en une autre figure convexe, de type carré, triangle, œuf, ovale ou polygone régulier.

En revanche — et c'est le second volet de la réponse au problème de quadrature par découpage de Tarski —, si l'on accepte que les morceaux puissent être des sous-ensembles quelconques du disque original, alors la réponse est positive. Cela découle d'un résultat de M. Laczkovich, qui propose d'ailleurs une recomposition du carré en n'effectuant que des translations à partir des pièces du disque découpé : la quadrature du cercle par découpage ensembliste est possible et ne nécessite que des translations. Le résultat de M. Laczkovich entraîne aussi que, si deux polygones quelconques ont la même aire, on peut découper le premier, déplacer ses pièces en n'effectuant que des trans­lations et recomposer le second.

Géométrie ensembliste

De tels découpages théoriques n'ont aucune traduction physique, et aucune figure de ce chapitre ne vous donnera une idée des pièces de M. Laczkovich qui réalisent la quadrature du cercle.

Pourquoi ? Parce que la preuve de leur existence utilise l'axiome du choix et que les pièces des découpages sont d'une telle complexité — pire que les fractales ! — qu'on ne peut pas les représenter de façon réaliste. De surcroît, le « découpage » du disque de M. Laczkovich comporte plus de 1050 pièces !

On sait que l'axiome du choix fut l'objet d'âpres discussions lors de la mise au point de la théorie des ensembles et de son adoption par les mathé­maticiens du début du XXe siècle.

Rappelons que l'axiome du choix affirme que, si E est un ensemble non vide d'ensembles non vides alors on peut constituer un nouvel ensemble en choisissant un élément dans chaque ensemble de E. Ainsi, à partir de l'ensemble $E = \{ \{a,b\},\{e,f\},\{g,h\},\{i,j\}\}$, on obtient par choix $\{a,f,h,j\}$. L'axiome du choix ne crée de difficultés que lorsque E est infini, ce qui est le cas en géométrie.

Ce n'est pas la première fois que les problèmes de découpage mettent le mathématicien utilisateur de l'axiome du choix dans une position inconfortable : le paradoxe de Banach-Tarski est un autre exemple de cette situation. Une sphère peut être décomposée en un nombre fini de morceaux, qui, une fois déplacés (sans déformation), se recomposent en deux sphères identiques à la sphère de départ !

Mais il nous faudra aller un peu plus loin dans les découpages dans l'espace pour se rendre compte que la situation y devient vraiment plus complexe... une histoire que vous retrouverez dans un prochain article sur CultureMath !