Sur la cheminée de mes parents trône un calendrier décoratif fait de morceaux de bois à déplacer chaque jour afin d'indiquer la date.

En pratique, l'objet se compose d'un support, de trois pièces allongées ayant chacune quatre faces marquées avec les mois de l'année (qui se placent au fond du support, une seule face étant visible) et, au-dessus d'elles, de deux cubes (donc avec $6$ faces) marqués avec un chiffre par face qui permettent d'indiquer les différentes dates avec les deux faces visibles. Voici une photo des deux cubes isolés :

L'intérêt de l'objet est a priori très limité... sauf qu'il est mathématiquement impossible de réaliser un tel calendrier.

Si vous êtes curieux, n'hésitez pas à chercher par vous-même avant d'aller plus loin car j'explique tout dans la suite du texte.

Mathématiquement impossible...

Pour bien comprendre la difficulté de ce calendrier, essayons de reconstruire les deux cubes, c'est-à-dire d'écrire tous les chiffres sur les faces, en tenant compte des contraintes imposées par le souhait de représenter les dates de $01$ à $31$. Initialement ces cubes n'ont aucun chiffre inscrit et l'on va indiquer petit à petit les chiffres qui apparaissent sur les cubes.

Remarquons tout d'abord que l'on doit pouvoir écrire les dates $11$ et $22$ avec ces deux cubes ; ainsi, les chiffres $1$ et $2$ sont nécessairement présents sur les deux ; la liste, partielle, des chiffres sur chaque dé est alors

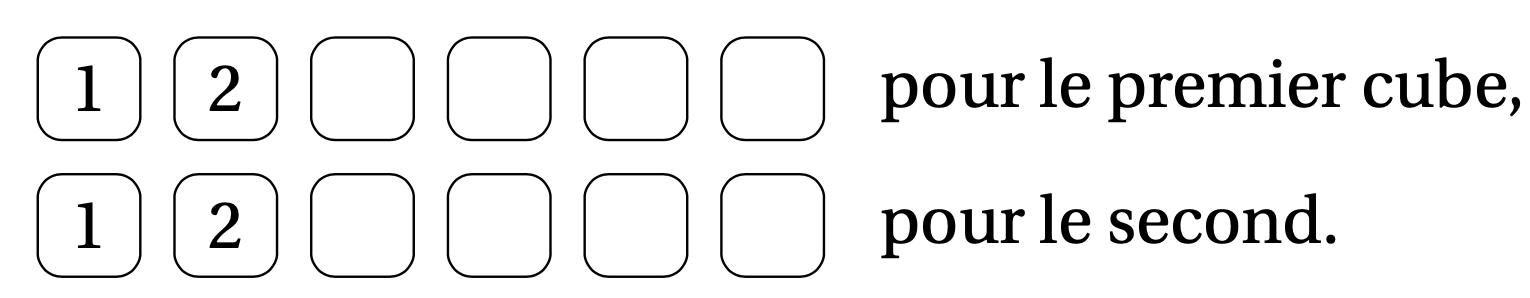
Il reste alors huit faces à remplir et huit chiffres nécessaires pour écrire les dates ($0$, $3$, $4$, $5$, $6$, $7$, $8$ et $9$). Il n'y a pour l'instant aucun problème. Plaçons le chiffre $0$ sur l'un des cubes, par exemple, le premier :

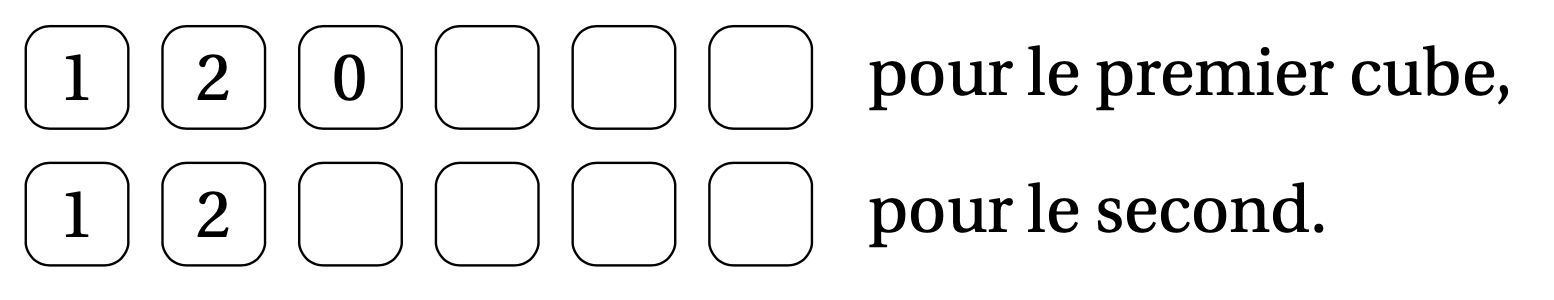
Pour que le calendrier soit utilisable en début de mois, il faut pouvoir réaliser les dates $01$, $02$ (que l'on sait déjà obtenir avec le $0$ du premier cube et le $1$ ou le $2$ du deuxième cube), mais aussi $03$, $04$, ..., $09$.

Si, pour toutes ces dates, on utilisait uniquement le $0$ du premier cube, on devrait trouver sur le deuxième cube, les chiffres $3$, $4$, ..., $9$. C'est problématique car il ne reste que quatre faces disponibles sur ce cube: on ne peut donc y placer les sept chiffres dont on a besoin.

La conclusion de ce petit raisonnement est que l'on n'utilise pas toujours le premier cube pour faire le $0$ dans les dates et donc, qu'il y aussi un $0$ sur le deuxième cube :

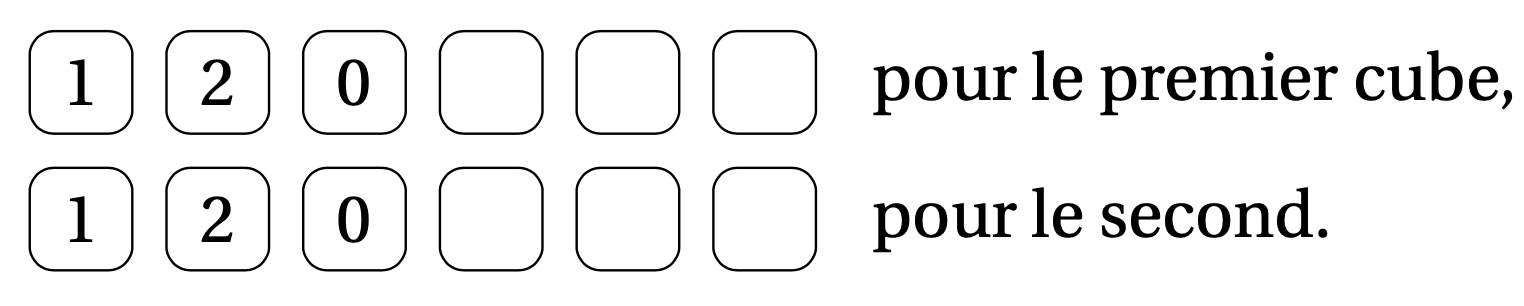
Désormais, il ne reste plus que six faces disponibles et il y a sept chiffres à écrire : il n'est pas possible de les écrire tous et donc certaines dates ne pourront pas être réalisées ; ce calendrier est donc mathématiquement incomplet !

... mais qui existe pourtant !

Le raisonnement de la partie précédente est correct et pourtant mes parents m'assurent qu'ils parviennent bien à indiquer toutes les dates avec leur calendrier. Pour comprendre cette apparente incohérence, regardons de plus près à quoi ressemblent les cubes dans le calendrier sur la cheminée ; avec les notations précédentes,

On constate immédiatement que cette façon de numéroter les faces des cubes ne contredit pas la conclusion de la partie précédente : un chiffre manque bien à l'appel, en l'occurrence le $9$.

L'« astuce » qui permet d'écrire toutes les dates est que, les dessins du $6$ et du $9$ sont symétriques : en tournant le dessin du $6$ on obtient le dessin du $9$ ; ainsi, on peut utiliser une seule même face pour représenter le chiffre $6$ et le chiffre $9$ par un simple retournement du cube.

Comme aucune date ne comporte à la fois un $6$ et un $9$, le tour est presque joué. Il vous reste à construire les cubes pour vérifier qu'on peut bien obtenir toutes les dates et donc, que le calendrier « mathématiquement impossible » fonctionne bien !