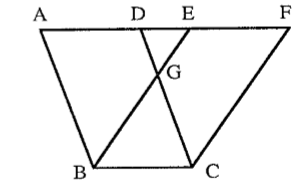
Après une longue absence les cas d’égalité des triangles ont fait leur retour dans les programmes du collège de 2015.
Activités pour la classe disponibles ici.
Ils avaient disparu avec la réforme des collèges mise en place en 1969. Ils ont fait une courte réapparition dans les programmes du lycée en 2001 pour disparaître de nouveau dans les programmes de 2009. Beaucoup d’enseignant⋅es de collège n’ont donc pas fréquenté cette notion, ni en tant qu’élève, ni pendant leurs études. Et pourtant, c’est un outil qui a été abondamment utilisé depuis l’Antiquité par les géomètres. Nous nous réjouissons de cette récente réapparition dans les programmes de collège, car nos élèves en phase d’apprentissage de la preuve ont été privé⋅es pendant trop longtemps d’un outil formateur et efficace.
Afin de faire percevoir le rôle fondamental de ces cas d’égalité en géométrie élémentaire, nous allons présenter quelques textes d’Euclide, de Thabit Ibn Qurra et de Clairaut, tout en nous attachant à décrire brièvement comment l’héritage d’Euclide s’est transmis de l’Antiquité jusqu’au XVIIIe siècle.
Les Éléments d'Euclide
D’Euclide, on ne sait quasiment rien. Nos principales sources sur son existence sont de petites anecdotes sujettes à différentes conjectures, relatées par Pappus (IVe siècle apr. J.-C), un des derniers grands mathématiciens grecs, et le philosophe néoplatonicien Proclus (environ 412,485). Il semblerait qu’Euclide ait vécu à Alexandrie au IIIe siècle avant Jésus-Christ.
Son ouvrage le plus connu intitulé les Éléments, comporte 13 livres essentiellement consacrés à la géométrie, sauf les livres V (théorie des proportions), VII, VIII et IX (arithmétique) et X (incommensurables). Ils suivent une structure axiomatico-déductive, modèle de rigueur pendant plus de 2000 ans. On peut faire l’hypothèse qu’Euclide a effectué une compilation de travaux antérieurs avec des ajouts personnels. La présentation que nous faisons ci-dessous s’appuie sur la version de Vitrac citée en bibliographie. Le livre I débute par 23 définitions, 5 demandes (ou postulats) et 9 notions communes (ce qui permet de raisonner). Suivent 48 propositions démontrées à l’aide des demandes, notions communes et/ou propositions précédentes. Ce livre se termine par le théorème actuellement connu sous le nom « de Pythagore » et sa réciproque. Dès le début du livre I on reconnaît un de nos cas d’égalité de deux triangles, c’est la proposition 4.
Proposition 4 : Si deux triangles ont deux côtés égaux à deux côtés chacun à chacun, et s'ils ont un angle égal à un angle, celui contenu par les droites égales, ils auront aussi la base égale à la base, les triangles seront égaux et les angles restants seront égaux aux angles restants, chacun à chacun, c'est-à-dire ceux que les côtés égaux sous-tendent.
Euclide en fait une justification par superposition d’une manière analogue à celle que l’on pourrait présenter dans les classes de collège. Cette proposition apparaît fondamentale dans la suite du livre I ; elle est explicitement utilisée dans la démonstration de 11 propositions, 10 d’entre elles étant des jalons indispensables pour les suivantes et la 11ème étant le théorème dit « de Pythagore ».
Le deuxième cas d’égalité d’Euclide apparaît en proposition 8.
Proposition 8 : Si deux triangles ont deux côtés égaux à deux côtés chacun à chacun, s’ils ont de plus la base égale à la base, ils auront aussi un angle égal, à savoir celui qui est contenu par les droites égales1.
On peut remarquer que cette conclusion de la proposition 8 n'énonce pas l'égalité des deux triangles et de tous les éléments correspondants. Stricto sensu, ce n'est pas un cas d'égalité des triangles. On peut observer la démarche minimaliste d’Euclide. Il utilisera la proposition 8 pour démontrer des égalités d’angles, comme dans la proposition 9 que nous présentons intégralement dans la version de Vitrac.
Proposition 9 : Couper un angle rectiligne donné en deux parties égales.
Démonstration : Soit l'angle rectiligne donné sous BAC. Il faut alors le couper en deux parties égales. Que soit pris au hasard le point D sur AB1. Et que, de AC, soit retranchée la droite AE, égale à AD (Prop. 3)2, et que DE soit jointe (Dem. 1)3. Que soit construit sur DE le triangle équilatéral DEF (Prop. 1)4, et que AF soit jointe (Dem. 1). Je dis que l'angle sous BAC est coupé en deux parties égales par la droite AF. En effet, puisque AD est égale à AE, que AF est commune, alors les deux DA, AF sont égales aux deux EA, AF, chacune à chacune. Et la base DF est égale à la base EF (Df. 20)5. Donc l'angle sous DAF est égal à l'angle sous EAF (Prop. 8). Donc l'angle rectiligne donné sous BAC est coupé en deux parties égales par la droite AF. Ce qu'il fallait faire.
Euclide propose ainsi des théorèmes et des problèmes de construction. Jusqu’à la proposition 26, qui est le dernier cas d’égalité, il donne principalement des résultats sur les triangles. L’objet des propositions 27 à 32 est la théorie des parallèles qui donne des résultats sur les angles alternes-internes et les angles correspondants. Cette section se termine par la proposition 32 qui est le théorème sur la somme des angles d’un triangle. Euclide peut ensuite aborder les parallélogrammes et les propositions 33 à 48 sont consacrées à la méthode des aires (comparer des aires par « puzzles abstraits » en utilisant souvent les cas d’égalité des triangles).
La proposition 35 qui sera beaucoup utilisée par Euclide dans la suite de ses Éléments est un exemple somptueux de la méthode des aires.
Proposition 35 : Les parallélogrammes qui sont sur la même base et dans les mêmes parallèles sont égaux entre eux.
Démonstration : Soient ABCD, EBCF des parallélogrammes sur la même base BC, et dans les mêmes parallèles AF, BC. Je dis que le parallélogramme ABCD est égal au parallélogramme EBCF. En effet, puisque ABCD est un parallélogramme, AD est égale à BC (Prop. 34). Alors pour la même raison EF est aussi égale à BC. De sorte que AD est aussi égale à EF (N.C. 1). Et DE est commune donc AE toute entière est égale à DF toute entière. Or AB est aussi égale à DC alors les deux EA, AB sont égales aux deux FD, DC, chacune à chacune. Et l'angle sous FDC est égal à l'angle sous EAB, l'extérieur à l'intérieur (Prop. 29). Donc la base EB est égale à la base FC et le triangle EAB sera égal au triangle DFC (Prop. 4). Que DGE soit retranché de part et d'autre : le trapèze restant ABGD est donc égal au trapèze restant EGCF (N.C. 3). Que le triangle GBC soit ajouté de part et d'autre : le parallélogramme ABCD tout entier est donc égal au parallélogramme EBCF tout entier (N.C. 2). Donc les parallélogrammes qui sont sur la même base et dans les mêmes parallèles sont égaux entre eux. Ce qu'il fallait démontrer.
Avant de quitter Euclide, remarquons que dans toutes les propositions citées nous retrouvons souvent le mot « égal ». Que recouvre-t-il pour Euclide ? La première réponse est qu’on n’en sait rien car la notion d’ « égalité » n’est pas définie d’une manière générale dans les Éléments. Les six premières notions communes qui fixent ce qu’on peut faire avec des « choses » égales (exemple NC1 : les choses égales à une même chose sont égales entre elles) apparaissent comme des axiomes de l’égalité et valent pour des grandeurs. Par exemple, nous avons vu dans la proposition 35 deux parallélogrammes équivalents en aires qu’Euclide nomme égaux et qui ne sont pas superposables. Pour Euclide l’égalité des triangles et des parallélogrammes mentionnés serait donc une égalité de grandeurs. Cependant, la NC 7, Et les choses qui s’ajustent les unes sur les autres sont égales entre elles, donne, elle, une condition suffisante pour que deux choses soient égales. Elle est utilisée pour démontrer le cas d’égalité de la proposition 4, qui se conclut par une égalité en tout : les 3 angles, les 3 longueurs des côtés, les aires.
Transmission des Éléments d'Euclide jusqu'au XVIIIe siècle
Les Éléments d’Euclide vont avoir un énorme succès dans le monde mathématique. Son traité va même devenir un genre littéraire que l’on désignera par le titre « Éléments de… ». Il a été traduit et commenté dans de nombreuses langues : arabe, latin, hébreu, syriaque. Le plus ancien manuscrit complet qui nous soit parvenu daterait du Xe siècle ; il se trouve dans les coffres de la Bibliothèque Vaticane. Il est écrit en grec.
Dès 775 les savants arabes sont en possession de copies du texte grec des Éléments. Ils ont été traduits, résumés et commentés en langue arabe dans une cinquantaine de travaux. Les savants y montrent un intérêt particulier pour la théorie des parallèles, la théorie des proportions, la théorie des irrationnels, et aussi la démonstration du 5ème postulat.
Les traces que nous ont laissées les Latins sont maigres. Ce sont des traductions d’extraits des Éléments du grec en latin.
En revanche, de nombreuses copies ont été effectuées au Moyen-Âge, ce sont essentiellement des traductions de l’arabe en latin. Les plus marquantes sont celles de Gérard de Crémone (1114-1187), Adélard de Bath (entre 1100 et 1130) et Campanus de Novare (1259). Campanus était un excellent mathématicien qui a composé la meilleure version latine de l’arabe du point de vue mathématique. Son édition comporte des commentaires pour expliquer ou clarifier les démonstrations.
Les débuts de la Renaissance sont marqués par l’invention de l’imprimerie. Sachant que les Éléments est l’ouvrage le plus édité dans le monde après la Bible à partir du XVe siècle, il est impossible d’être exhaustif dans la présentation des différentes éditions durant la Renaissance. Nous en retiendrons quatre.
La première impression des Éléments a lieu en 1482 à Venise. C’est la version de Campanus qui a cet honneur et c’est le premier livre mathématique d’importance à être imprimé.
La chute de Constantinople en 1453 va aussi influer sur la transmission des Éléments ; dès la fin du XVe siècle, des manuscrits des Éléments écrits en grec font leur apparition en Italie. L’édition de Campanus suscite alors des débats concernant les mérites respectifs des traductions du grec ou de l’arabe. Zamberti travaille pendant 7 ans à une traduction du grec en latin et fait paraître son texte en 1505 dans lequel il se montre très hostile à Campanus en lui reprochant d’omettre ou de changer le texte d’Euclide.
L'édition princeps des Éléments d'Euclide paraît à Bâle en 1530 : elle est due au théologien Simon Grynaeus l'aîné (mort en 1541). Elle s’appuie sur deux manuscrits identifiés comme pouvant être rangés parmi les plus mauvais. Elle fut cependant la seule édition complète du grec jusqu'au XVIIIe siècle.
La querelle Campanus-Zamberti ne s’éteindra qu'avec la version latine des XV Livres de Federigo Commandinus d'Urbino (1509-1575) parue à Pesaro en 1572. Commandinus est probablement, de tous les éditeurs renaissants d'Euclide, le mathématicien le plus compétent. Il utilise l'édition princeps et au moins un autre manuscrit grec non identifié. C'est la première version basée sur un original grec acceptable du point de vue critique. L'importance de son travail fut considérable jusqu'au XIXe siècle.
A la Renaissance le latin domine, mais dès 1540 on voit apparaître des traductions en langue vernaculaire. Dans l’ordre chronologique d’apparition : italien, toscan, allemand, français, espagnol, puis tardivement hollandais.
Durant cette période, c’est surtout l’identité d’Euclide qui fait débat. On se pose des questions : à quelle époque a-t-il vécu ? Quel est son rôle dans la rédaction des Éléments ? Certains attribuent les énoncés à Euclide et les démonstrations à Théon d’Alexandrie (335-405), d’autres affirment qu’Euclide ne serait pas responsable de l’ordre des propositions. Du coup on se permet de changer l’ordre, de réécrire les démonstrations, de publier des versions avec des nombres, de supprimer des démonstrations.
Un événement se produit alors : c’est la parution en 1574 (rééd. 1589, 1591, 1603, 1607, 1612) à Rome de la version latine des Éléments de Clavius (1537-1612). C’est une recension qui comporte 16 livres et qui est fondée sur Campanus, Zamberti et Commandinus. Les preuves réécrites, les éclaircissements apportés, les notes (recueillies chez les éditeurs et commentateurs) ajoutées en font un ouvrage de grande valeur. Grâce à Clavius, le XVIIe siècle allait disposer d’Éléments mathématiquement instructifs.
Au XVIIe siècle apparaissent de nouvelles critiques sur les Anciens. En particulier pour les Éléments, la présentation des propositions est remise en question. Il est mis en avant que le fait de démontrer des résultats sans en présenter l’heuristique ne donne pas de méthodes pour trouver des résultats nouveaux. La question de la méthode est une préoccupation de René Descartes (1596-1650) qui écrit dans l’introduction de son ouvrage Discours de la méthode (1637) lorsqu’il présente les quatre préceptes de sa logique: « Le troisième [précepte est] de conduire par ordre mes pensées, en commençant par les objets les plus simples, et les plus aisées à connaître, pour montrer peu à peu comme par degrés jusqu’à la connaissance des plus composés ». C’est suivant ces préceptes qu’il va construire son ouvrage La Géométrie, appendice au Discours de la méthode, dans lequel il s’attache à donner des méthodes générales pour résoudre des problèmes. L’idée de « conduire par ordre [ses] pensées » inspire à Antoine Arnauld (1612-1694) un ordre très différent de celui d’Euclide pour ses Nouveaux Éléments de géométrie (1667).
La démonstration du théorème de Pythagore par Clairaut et par Qurra
Les préoccupations d’Alexis Claude Clairaut (1713-1765), un des plus grands mathématiciens du XVIIIe siècle, sont d’une nature tout à fait différente. Il explique dans la préface de son ouvrage Éléments de géométrie (1753) que les Éléments d’Euclide sont trop abstraits, que leur lecture n’est pas motivante pour les débutants, elle est même rebutante et la structure axiomatico-déductive choisie par Euclide (définitions, postulats, axiomes, propositions) empêche le lecteur de comprendre ce qu’on veut lui enseigner. Ce souci des commençants nous semble très moderne. Sa modernité ne se dément pas lorsqu’il justifie le choix de sa progression. Il s’agit de suivre « une route semblable à celle des inventeurs de la géométrie », selon ses propres termes. Il motivera les élèves par des problèmes sur des calculs de mesure des terrains, comme la géométrie aurait débuté dans l’histoire selon lui, et ensuite il passera à des recherches plus générales, plus abstraites, mais qui présenteront une analogie avec les premières, c’est-à-dire qu’il adoptera une approche par résolution de problèmes. Cette démarche est illustrée dans les propositions XV, XVI, XVII, XVIII, XIX de la seconde partie de ses Éléments. Citons la fin de la proposition XV : « mais, ce qu’on ne pouvait guère manquer de se proposer, […] c’est de faire un quarré égal à deux autres. » Nous reproduisons ci-dessous la proposition XVI et le début de la proposition XVII ainsi que les schémas associés figurant dans les Éléments de Clairaut :
On constate dans la proposition XVII qu’il cherche à appliquer les préceptes donnés en introduction : ne pas présenter les choses d’une manière sèche comme Euclide, et montrer une heuristique de sa démonstration. Celle-là consiste à s’appuyer sur le cas simple de la proposition XVI et de tenter de le généraliser. Il va s’agir de trouver un point H qui joue le rôle du point C de la proposition XVI. Voici un résumé de sa démonstration. Il propose donc de placer H tel que DH soit égal au côté CF et de faire tourner le triangle ADH autour du point A de sorte qu’il atteigne la position Adh. La distance Ch sera égale à DF. Lorsqu’on fait tourner le triangle EFH autour du point E pour prendre la position Efh, le point H arrivera au même point h. Les figures ADFEfd et AHEh seront équivalentes en aire. Il termine en prouvant que AHEh est un carré.
Clairaut poursuit par la proposition XVIII dans laquelle on reconnaît le théorème « de Pythagore ».
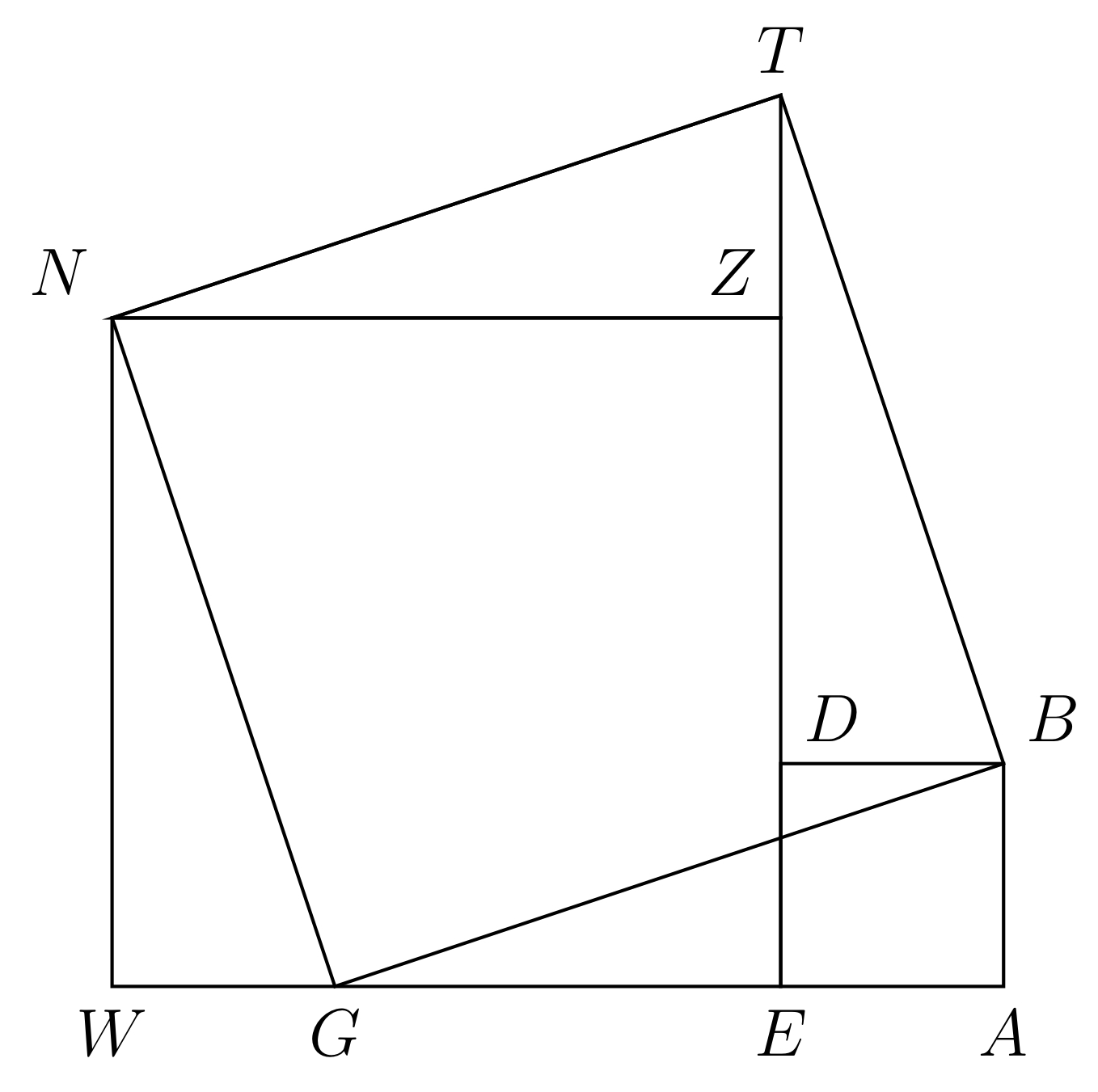
La démonstration de Clairaut utilise le mouvement, mais les cas d’égalités des triangles sont un outil tout aussi bien adapté à cette situation. En voici pour preuve la démonstration du théorème dit « de Pythagore », présentée par le mathématicien arabe Thabit Ibn Qurra (836-901) neuf siècles auparavant dans son Épître sur la preuve attribuée à Socrate au sujet du quarré et de sa diagonale. Nous nous appuyons ici sur la traduction d’Ahmed Djebbar.
Proposition : Pour tout triangle à angle droit, les carrés de ses deux côtés qui entourent son angle droit sont, lorsqu’ils sont ajoutés, égaux au carré du côté qui en est la corde.
Soit le triangle ABG, à angle droit, et BAG son angle droit. Je dis que les carrés de AB et AG, s’ils sont ajoutés, sont égaux au carré de côté BG.
Démonstration résumée : On construit le carré ABDE et le point W sur (AG) tel que EW = AG. On construit de même le carré EZHW et le point T sur (EZ) tel que DT = AG. Les 4 triangles BAG, BDT, TZH, GWH ont un angle droit et les côtés qui entourent leurs angles droits sont égaux 2 à 2. Les 4 triangles sont donc égaux. Il démontre ensuite que GTBH est un carré (4 côtés égaux et 2 angles droits). L’ensemble de la figure GBDZH avec les 2 triangles ABG et GWH, et qui sont les 2 carrés ABDE, EWHZ, est égale à l’ensemble de la figure GBDZH avec les 2 triangles BDT, ZTH, et qui est le carré BGTH. Donc les carrés des 2 côtés AB, AG, s’ils sont ajoutés, sont égaux au carré du côté BG.
Les démonstrations de Clairaut ou de Thabit Ibn Qurra du théorème « de Pythagore » sont basées sur le principe d’un puzzle abstrait comme celle d’Euclide, mais elles sont beaucoup plus simples que la sienne.
Remarquons que, fidèle à sa méthode pédagogique, Clairaut ne commence pas par donner le théorème, mais il résout un problème de géométrie (construire un carré équivalent en aire à la figure formée par 2 carrés donnés, problème qui peut être une préoccupation concrète). Le théorème « de Pythagore » apparaît comme cerise sur le gâteau à la fin de la démonstration.
A la fin du XVIIIe, on assistera à un retour à l’ordre et à la rigueur euclidiens grâce à Adrien-Marie Legendre (1752-1833) qui le mettra en œuvre dans son ouvrage Éléments de géométrie, grand succès de l’édition scolaire (12 éditions de 1794 à 1823).
L’apparition de nouvelles géométries (de Lobatchevski, de Riemann, et géométrie projective) fait éclore au XIXe siècle la question des fondements de la géométrie classique. Les travaux de David Hilbert (1862-1943) portent sur les fondements des mathématiques et en particulier de la géométrie. Dans Les fondements de la géométrie (1899) Hilbert a le projet de « constituer, pour la géométrie, un système complet d’axiomes aussi simples que possible et d’en déduire les théorèmes les plus importants, de façon à mettre en évidence le rôle des divers groupes d’axiomes et la portée de chacun d’eux. » Hilbert classe les axiomes en 5 groupes : appartenance, ordre, congruences, parallèles, continuité. Le cinquième axiome de congruence énonce : « Si dans deux triangles ABC et A’B’C’ les congruences suivantes sont satisfaites : AB = A’B’, AC = A’C’, angle BAC = angle B’A’C’, la congruence angle ABC = angle A’B’C’ l’est aussi. » Cet axiome lui permet de démontrer le 1er cas de congruence (nous dirions d’égalité) des triangles, grâce à l’axiome précédent sur l’univocité du report d’un angle. Ainsi Hilbert peut-il évacuer l’utilisation d’un transport du triangle pour la démonstration de la proposition I-4 d’Euclide, mouvement qui a parfois gêné aussi bien ses contemporains que les mathématiciens ultérieurs.
Bibliographie
Clairaut, Alexis. Éléments de géométrie. 1753. Disponible sur internet en cliquant ici.
Descartes, René. Discours de la méthode pour bien conduire sa raison et chercher la vérité dans les sciences, plus la dioptrique, les météores et la géométrie qui sont des essais de cette méthode. 1637. Disponible sur Gallica : cliquer ici.
[1] Euclide. Les Éléments, traduits du texte de Heiberg. Introduction générale par Maurice Caveing. Livres I-IV : Géométrie plane, traduction et commentaires de Bernard Vitrac. Paris : PUF, 1990. Disponible sur la page personnelle de Bernard Vitrac : cliquer ici.
[2] Euclide. Les œuvres d’Euclide, traduction de François Peyrard, 3 volumes. Paris : chez M. Patris, 1814 (vol.1), 1816 (vol.2), 1818 (vol.3). Disponible en ligne sur Internet Archive : cliquer ici. Œuvre partiellement numérisée (édition 1804) par Marc Szwajcer. Site : cliquer ici.
Hilbert, David. Les principes fondamentaux de la géométrie, traduits par L. Laugel. Ed. Gauthier-Villars Paris 1900.
Kouteynikoff Odile, Loget François, Moyon Marc. Quelques lectures renaissantes des Éléments d'Euclide. Barbin Evelyne & Moyon Marc. Les ouvrages de mathématiques dans l'histoire. Entre recherche, enseignement et culture, PULIM, pp.13-28, 2013, Savoirs Scientifiques et Pratiques d'Enseignement. Disponible sur internet : cliquer ici.
Pappus, Collection Mathématique, traduction Paul Ver Eecke (1933), ré-édition Blanchard, Paris, 1982.
Proclus de Lycie, Les commentaires sur le premier livre des Eléments d’Euclide traduits du grec par Paul Ver Eecke (1948). Réédition IREM de Lille.
Thabit Ibn Qurra, Epître sur la preuve attribuée à Socrate au sujet du quarré et de sa diagonale, traduit et présenté par Ahmed Djebbar in Textes géométriques arabes (IXème-XVème), pour la journée sur la phase arabe de la géométrie de l’IREM de Dijon (10 décembre 2009).
Site du groupe M.ATH de l'IREM de Paris, Dossier thématique « Histoire et Géométrie » : cliquer ici.