Avec les $n$ personnes présentes au repas, est-il possible d'effectuer toutes les combinaisons possibles de photos durant le repas ?
En tant que mathématiciens, un problème de dénombrement s'offre alors à nous en attendant la fin de la séance photo.

La réforme du lycée intègre les combinaisons et les arrangements dans le programme de Terminale. Cet article peut aider à faire comprendre ces notions aux plus réticents de la combinatoire, professeurs ou étudiants, car il s'appuie sur un cadre très concret. Il va plus loin en s'intéressant à deux formules de somme d'éléments combinatoires, dont l'une est classique et l'autre démontrée dans cet article.

En plus d'être une piqûre de rappel des bases du dénombrement utiles à la réforme du baccalauréat, cet article peut être réadapté pour des problèmes de Maths Sup, Maths Spé ou Licence voire pour un problème d'approfondissement en Terminale.

Arrangements et combinaisons

Soit $n\in\mathbb{N}^*$ et $E$ un ensemble à $n$ éléments (pouvant représenter les $n$ personnes présentes au repas).

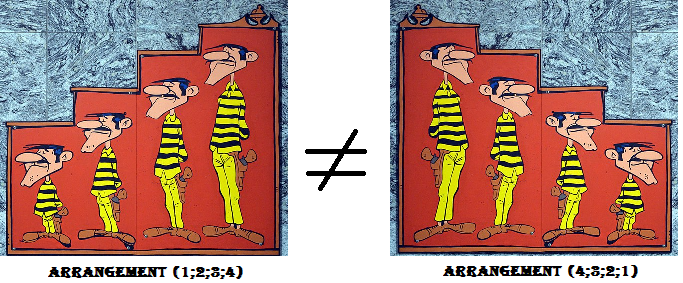
Par exemple, les 3-listes $(1;2;3)$ et $(3;2;1)$ sont deux arrangements distincts de 3 éléments de $E=[\![1;10 ]\!]$ tandis que les ensembles $\{1;2;3\}$ et $\{3;2;1\}$ sont égaux et forment une seule combinaison de 3 éléments de $E$.

La preuve est assez rapide. Si $1\leq p \leq n$, alors pour former une liste ordonnée de $p$ éléments distincts choisis parmi $n$, nous avons $n$ choix pour le premier élément, puis $n-1$ choix pour le deuxième, ... puis $n-p+1$ choix pour le $p^{\, ième}$, soit $n(n-1)\ldots(n-p+1)=\dfrac{n!}{(n-p)!}$ choix au total.

Vous remarquerez que la définition est étendue au cas où $p=0$. Dans ce cas, un arrangement de $0$ élément est unique et c'est la liste "vide". $\square$

La preuve repose sur le fait que le nombre de manières pour ordonner $p$ éléments distincts est $p!$. Ainsi, avec chacune des $\binom{n}{p}$ combinaisons de $p$ éléments parmi $n$, on peut former $p!$ listes ordonnées différentes de $p$ éléments, soit au total $p! \times \binom{n}{p}$. Ainsi, $A_n^p=p! \times \binom{n}{p}$ d'où $\displaystyle \binom{n}{p}=\dfrac{A_n^p}{p!}=\dfrac{n!}{p!(n-p)!}$. $\square$

Dénombrer des photos sans s'intéresser à l'ordre des individus

Notons $E=\{1;\ldots;n\}$ l'ensemble des $n$ individus présents au repas. Cette section s'intéresse au dénombrement des photos réalisables sans donner d'importance à la position des individus sur la photo. Nous utiliserons alors la notion de combinaisons. Par exemple, la combinaison $P=\{2;3;5\}$ de 3 éléments de $E$ modélise la photo dans laquelle apparaissent uniquement les individus 2, 3 et 5. $P=\emptyset$ est la photo sans intérêt ne comportant aucun individu, tandis que $P=E$ est la photo contenant les $n$ individus.

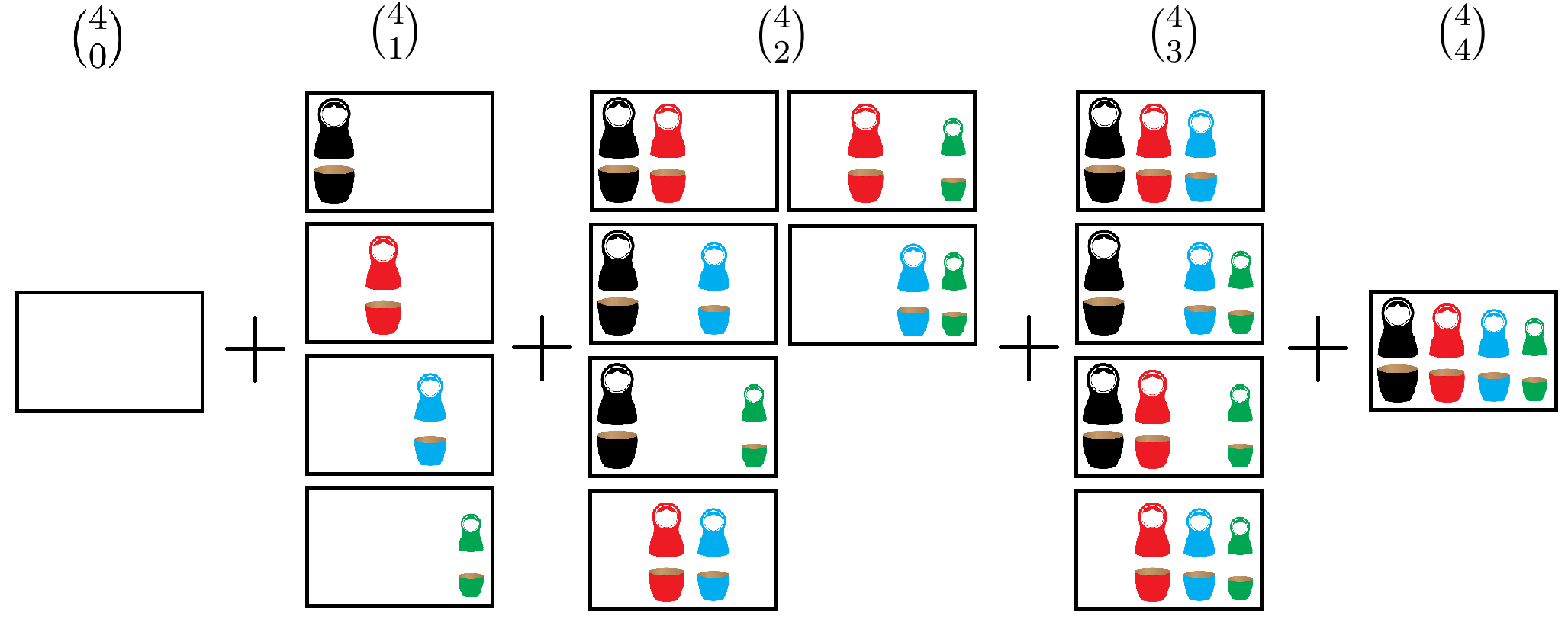
Le nombre total de photos réalisables s'obtient alors grâce à la somme suivante :

\[\sum_{p=0}^{n}\binom{n}{p}\]

En effet, il y a $\binom{n}{0}$ photos comportant $0$ individu parmi les $n$, $\binom{n}{1}$ photos comportant $1$ individu parmi les $n$, $\binom{n}{2}$ photos comportant $2$ individus parmi les $n$ ... et ainsi de suite jusqu'à la combinaison de $n$ individus parmi les $n$ (cf. FIGURE 1).

En utilisant la fameuse formule du binôme de Newton,

\[ \sum_{p=0}^{n}\binom{n}{p} = \sum_{p=0}^{n}\binom{n}{p}1^p1^{n-p}=(1+1)^n=2^n\]

On dénombre alors $2^n$ combinaisons/photographies différentes à partir de $n$ individus, soit tout de même $1024$ photos différentes avec $n=10$ individus et $1\, 048\, 576$ photos pour un repas de famille regroupant seulement $20$ personnes. Qui aurait imaginé que le nombre de combinaisons possibles serait si grand ? On comprend alors mieux pourquoi les séances photos sont si longues !

Une autre vision du dénombrement des combinaisons toutes tailles confondues est une approche binaire. Considérons un nombre binaire à $n$ bits, où le $i^{\, ème}$ bit est à 1 si l'individu numéro $i$ est présent sur la photo et à 0 sinon. Ainsi, $11010\ldots0$ est associée à la photo où seuls les individus numéro 1, 2 et 4 apparaissent. Il est clair que deux nombres binaires différents représentent des photographies différentes. Comme il y a $2^n$ nombres binaires distincts à $n$ bits, il y a $2^n$ photos possibles.

Dénombrer des photos en tenant compte de l'ordre

Dans cette dernière partie, on ne s'intéresse plus seulement au contenu des photos (individus présents) mais aussi à l'arrangement des personnes au sein des photos. Autrement dit, la photo constituée de tonton (à gauche) et tata (à droite) sera différente de la photo constituée de tata (à gauche) et tonton (à droite). Dès lors que l'ordre intervient, les photos sont modélisées par des arrangements d'éléments de $E$.

Ainsi, compter les arrangements toutes tailles confondues revient à sommer le nombre d'arrangements de $p$ éléments parmi $n$ pour $p$ variant de $0$ à $n$. Le nombre total de photos réalisables s'exprime donc ainsi :

\[\sum_{p=0}^{n}A_n^p\]

Il serait sympathique d'obtenir une formule explicite du nombre total de photos/arrangements à l'instar de la partie précédente. On peut démontrer la jolie formule de la propriété 4 dessous, qui peut être donnée en exercice de Maths Sup, Spé ou Licence voire dans un problème d'approfondissement en Terminale. Sa preuve nécessite de majorer la suite des restes d'indice $n$ de la série exponentielle $\displaystyle \sum_{n\geqslant 0}\dfrac{1}{n!}$. Le lemme suivant donne une telle majoration.

Preuve du Lemme.

Considérons les deux suites $(u_n)_{n>0}$ et $(w_n)_{n>0}$ définies par :

\[u_n=\displaystyle \sum_{p=0}^{n}\dfrac{1}{p!} \quad \text{et} \quad w_n=\displaystyle \sum_{p=0}^{n-1}\dfrac{1}{p!}+\dfrac{2}{n!} .\]

Il est facile de vérifier que $(u_n)$ est strictement croissante. Vérifions que $(w_n)_{n>0}$ est strictement décroissante à partir du rang $n=2$.

\begin{align*}
w_{n+1}-w_n &=\displaystyle \sum_{p=0}^{n}\dfrac{1}{p!}+\dfrac{2}{(n+1)!}-\displaystyle \sum_{p=0}^{n-1}\dfrac{1}{p!}-\dfrac{2}{n!}\\
&=\dfrac{1}{n!}+\dfrac{2}{(n+1)!}-\dfrac{2}{n!}\\
&=\dfrac{1-n}{(n+1)!} \lt 0 \quad \text{pour} \quad n \gt 1
\end{align*}

On montre facilement que les suites $u$ et $v$ vérifient $\lim\limits_{n \rightarrow + \infty}(u_n-w_n)=0$ et par conséquent qu'elles sont adjacentes et de même limite $e$. On a donc pour tout $n \geq 2 $, $ u_n \lt e \lt w_n $ ($\star$). Les inégalités sont bien strictes car une suite strictement monotone et convergente n'atteint jamais sa limite (un raisonnement par l'absurde permet de le prouver). L'inégalité ($\star$) reste d'ailleurs vraie pour $n=1$.

Ainsi, en utilisant l'inégalité ($\star$), pour tout $n\geqslant 1$,

\[ e-\displaystyle \sum_{p=0}^{n}\dfrac{1}{p!}=e-u_n\lt w_n-u_n=\dfrac{1}{n!}\]

ce qui prouve le résultat du lemme. $\square$

Preuve.

Soit $n\in \mathbb{N}^*$. Notons $S_n=\displaystyle \sum_{p=0}^{n}A_n^p$.

$S_n \in\mathbb{N}$ car c'est une somme d'entiers donc par définition de la partie entière, nous devons démontrer que : $\forall n\in\mathbb{N}^*,$ $S_n\leq e\times n! \lt S_n+1$.

► Nous pouvons noter que $S_n=\displaystyle \sum_{p=0}^{n}\dfrac{n!}{(n-p)!}=\displaystyle \sum_{p=0}^{n}\dfrac{n!}{p!}$ par le renversement d'indice $p\mapsto n-p$. D'où $S_n=n! \times \displaystyle \sum_{p=0}^{n}\dfrac{1}{p!}$.

► Démontrons l'inégalité de gauche.

$\displaystyle \sum_{p=0}^{n}\dfrac{1}{p!}$ est la somme partielle d'indice $n$ d'une série exponentielle (à termes positifs) convergente de somme $e$. Ainsi : $\displaystyle \sum_{p=0}^{n}\dfrac{1}{p!}\leqslant e$,  soit $\dfrac{S_n}{n!}\leqslant e$, et finalement $S_n\leqslant e\times n!$.

► Démontrons l'inégalité de droite.

D'après le lemme, nous savons que pour tout $n\in\mathbb{N}^*$, $e-\displaystyle \sum_{p=0}^{n}\dfrac{1}{p!} \lt \dfrac{1}{n!}$. En multipliant cette inégalité par $n!$, nous obtenons $e\times n! -n!\times \displaystyle \sum_{p=0}^{n}\dfrac{1}{p!} \lt 1 $ autrement dit $e\times n! \lt S_n+1.$

► Nous avons donc prouvé que $\forall n\in\mathbb{N}^*,$ $S_n\leqslant e\times n! \lt S_n+1$. Par définition de la partie entière,

\begin{equation*}S_n=\lfloor e\times n! \rfloor . \; {\color{red} \square} \end{equation*}

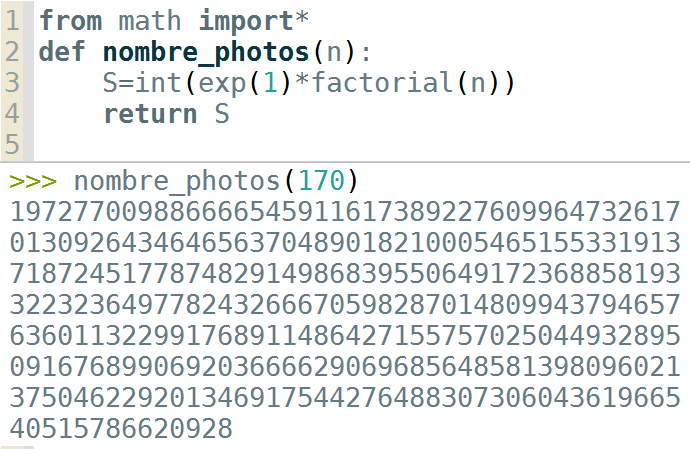
A l'aide d'une fonction Python (cf. FIGURE 3), on peut effectuer quelques applications numériques. Avec $n=10$ personnes, il est possible de former $\lfloor e\times 10!\rfloor = 9\, 864\, 101$ photos différentes et $6 613 313 319 248 079 872$ photos différentes avec $n=20$ personnes. La croissance du nombre d'arrangements en $n!$ est bien plus rapide que la croissance exponentielle du nombre de combinaisons ($q^n=o(n!)$ pour $n\rightarrow +\infty$). Encore plus irréaliste de prendre toutes les photos différentes lors d'un repas de famille si l'on est obsédé par l'ordre !

Conclusion et ouvertures

Pour conclure, le nombre total de photos réalisables en fonction du nombre $n$ d'individus présents "explose" de manière exponentielle (base 2) lorsque l'on ne tient pas compte de l'ordre des individus sur les photos et "en $n!$" dans le cas contraire. Ceci permet de répondre à la question introductive. D'une part, vous serez limité en mémoire de stockage et d'autre part, il faudra vous munir d'une patience hors du commun. Toute une vie ne suffirait même pas dans certains cas.

Le contexte des photos est très spécifique mais cette théorie a de nombreuses applications. Nous pouvons par exemple répondre à des questions du type : « Combien de phrases sans répétition de mot pouvons-nous former à partir de tous les mots du dictionnaire ? à partir de 20 mots différents ? » ou « Combien de caractères différents peuvent être représentés en braille ? »