Les invariants

N'est-on pas rassuré de découvrir quelque chose d'immuable, d'invariant, dans un problème complexe ? C'est le cas en mathématiques comme l'illustre ce premier exemple, très classique. Le nombre de façons de choisir $p$ éléments parmi $n$ est donné par le coefficient binomial 1 : \[\binom np=\frac{n!}{p!(n-p)!}.\] Cette formule, élégamment transcrite avec des factorielles, ne se prête pas au calcul à la main. On peut cependant en simplifier le numérateur par le facteur $(n-p)!$ du dénominateur et ramener l'ensemble au quotient de deux produits alignant chacun $p$ termes. Soit : \[\binom np=\frac{n(n-1)(n-2)\cdots ((n-p)+1)}{p(p-1)(p-2)\cdots1}.\] Au second membre, il est fréquent d'hésiter sur le dernier numérateur : s'agit-il de $(n-p)$ ? de $(n-p)-1$ ? de $(n-p)+1$ ? Chacun aura son « petit truc » pour s'en rappeler. En voici un. Scindons le second membre en \[\frac np\times\frac{n-1}{p-1}\times\frac{n-2}{p-2}\times\cdots\times\frac{(n-p)+1}{1}\] et songeons que d'une fraction à la suivante, numérateur et dénominateur décroissent au même rythme — ils perdent chacun une unité. Aussi, l'écart entre les deux vaut-il constamment, invariablement, $n-p$. De fait, \[n-p = (n-1)-(p-1)=(n-2)-(p-2)=\cdots\] À ce compte, le dernier numérateur n'est autre que $(n-p)+1$.

On retrouve une idée similaire dans 2. Il y faut réduire une tablette de chocolat jusqu'à séparer tous ses petits carreaux. On considérera qu'à chaque division, l'intégralité d'une ligne ou d'une colonne se casse. On se demande combien d'opérations sont alors nécessaires. Évidemment, rien n'indique a priori que leur nombre soit toujours le même : il y a tant de manières d'arriver à ce but ! Pourtant, un invariant ressort : la différence $m-c$ entre le nombre total $m$ de morceaux déjà obtenus et le nombre total $c$ de coupes déjà effectuées au cours de l'expérience. En effet, toute nouvelle division engendre un morceau supplémentaire si bien qu'invariablement, $m-c=1$. Si la plaquette compte $n$ carrés, on poursuit le processus pour $m=1$, $m=2$,..., jusqu'à $m=n$. Donc $n-1$ coupes exactement la décomposent entièrement.

Les invariants peuvent ainsi constituer des pièces maîtresses dans une démonstration. On les utilise autant pour l'étude des transformations géométriques, sur la caractéristique d'Euler dont découle la notion de genre d'une surface que, bien sûr, en logique et en informatique.

Les chevaliers de la table ronde

Concentrons-nous dans cette partie sur cet autre problème dans lequel repérage et rôle des invariants s'avèrent indispensables tant se bousculent les hypothèses. Accessible dès le lycée en classe de Numérique & Sciences Informatiques (NSI) 3 comme de mathématiques 4 il admet, du reste, plusieurs versions 56. Voici la plus connue :

La simulation en JavaScript/JSXGraph qui suit, réalisée pour la circonstance, préfigure ce que pourrait être leur début de soirée ($N=10$, cocher l'option Marche aléatoire).

Mais on aura bien du mal à cerner l'étendue des possibles. Chaque chevalier ayant toujours $2$ choix qui s'offrent à lui, $2^{10}=1\,024$ mouvements rendent compte du premier temps de la danse, conduisant certes à des configurations parfois isométriques (identiques à rotation ou symétrie près). Le deuxième temps multiplie ces $1\,024$ configurations à $1\,024$ autres, le troisième aussi, etc. Bref, la combinatoire s'envole et l'on ne saurait tester une à une toutes les chorégraphies.

C'est ici que les invariants viennent à notre secours ! Numérotons les places de $1$ à $10$, la place $1$ venant après la $10$ puisque la table est ronde. D'un coup de sa baguette magique, Merlin nous invite à considérer le nombre de chevaliers qui se trouvent sur une place paire. Au début, 5 chevaliers occupent une place paire et 5 une impaire. Or à chaque changement, ceux qui occupaient une place paire vont sur une place impaire et vice-versa. Ainsi et malgré ces chassez-croisés, 5 chevaliers demeurent invariablement sur une place paire. Il ne pourra donc jamais se trouver 10 chevaliers à la même place !

La question se généralise avec $N=2n$ chevaliers réunis autour de la table ; la réponse reste négative pour les mêmes raisons d'invariance et de parité. Mais que se passe-t-il si Arthur se joint à la fête ? Il y a désormais $N=2n+1$ personnes et surtout la place $2n+1$, numéro impair, est voisine de la place $1$, numéro impair également : l'invariant de parité n'opère plus.

Pas de panique ! Exploitons au contraire cet « inconvénient ». Diminuons le nombre de chevaliers occupant une place paire en invitant l'assemblée à rejoindre progressivement l'une des deux places $1$ ou $2n+1$. Ces emplacements pris, on peut ne plus s'en écarter grâce à des pas de côtés alternant la gauche et la droite. Et attendre les derniers. Une fois tout le monde regroupé, il n'y plus qu'à évoluer petit à petit vers la place médiane, numérotée $n+1$ (qui n'existe pas lorsque il y a un nombre pair de places), en contournant par un côté ou l'autre selon qu'on était situé en position $1$ ou $2n+1$. Le tableau de la figure 1 consigne, étape par étape et sur un exemple, la position occupée par tel ou tel chevalier jusqu'à ce que tous convergent au même endroit.

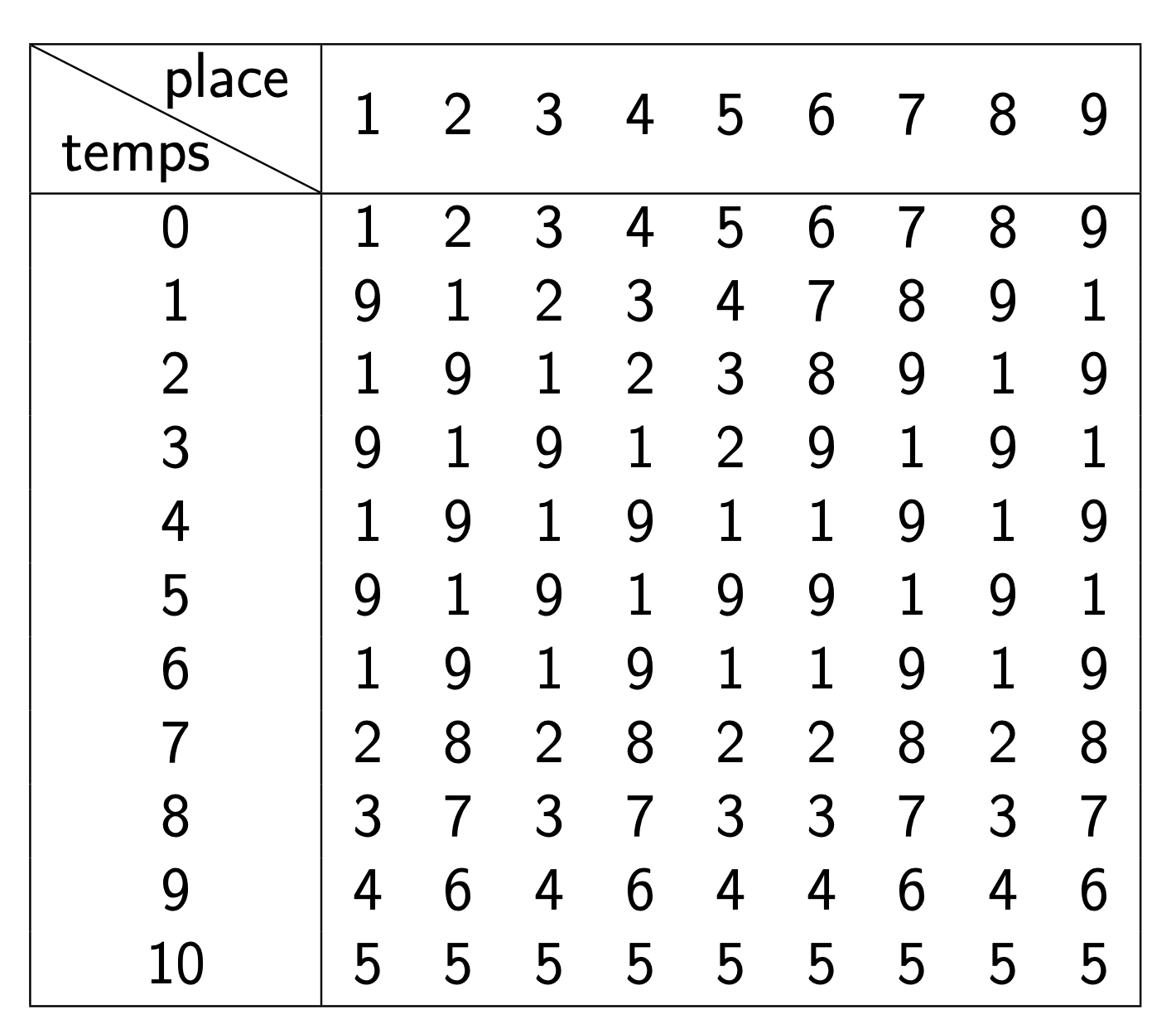
Bien appliqué — ce qui n'est pas le cas du tableau de la figure 1 où l'on fait patienter exagérément les chevaliers aux places $1$ et $2n+1$ — cet algorithme termine en $2n$ étapes. En effet, $n$ étapes sont nécessaires pour que les chevaliers, et notamment le $n+1$-ième, s'installent aux places $1$ ou $2n+1$. Puis s'y ajoutent $n$ autres étapes avant d'atteindre la place $n+1$. L'animation JavaScript/JSXGraph en rend compte (choisir par exemple $N=11$ et cocher l'option Algorithme).

On peut interroger l'optimalité de cet algorithme : existe-t-il une meilleure stratégie terminant en moins de $2n$ étapes ? Et bien non ! Voyons pourquoi...

Fixons arbitrairement la position finale au numéro $n+1$ comme dans la situation précédente. Cela ne change en rien notre raisonnement puisqu'on pourrait tout renuméroter a posteriori. Un algorithme minimal s'exécutant en $2n$ étapes au plus, aucun chevalier ne fait un tour complet — ceci consommerait $2n+1$ étapes au moins.

Soit un algorithme minimal. Il comporte $m$ étapes, avec $m \leq 2n$. Suivons le déplacement d'un chevalier. Codons chacun de ses mouvements dans le sens trigonométrique par la lettre $T$, et chacun de ses mouvements inverses par la lettre $\overline{T}$. La trajectoire qu'observe le chevalier se résume à une succession de symboles $T$ et $\overline{T}$. Cette séquence est de longueur $m$ exactement puisque le chevalier est toujours en mouvement. L'ordre dans lequel les symboles $T$ et $\overline{T}$ s'enchaînent pourrait être modifié, cela ne changerait pas le point d'arrivée. Quitte à les rapprocher, un symbole $T$ et un symbole $\overline{T}$ se neutralisent. Par l'esprit, on peut ainsi réduire le parcours du chevalier à une suite ne contenant que des $T$ ou que des $\overline{T}$.

• Ceci vaut en particulier pour le chevalier $n+1$. Déjà bien implanté, mais interdit de décrire le cadran, sa séquence réduite est vide. Son parcours compte autant de $T$ que de $\overline{T}$. Si bien que $m$ est pair.
• Ceci vaut aussi pour le chevalier $n$. Sa séquence réduite étant paire, elle ne peut valoir $(T)$. Puisque le chevalier ne décrit pas le cadran, il doit tourner dans l'autre sens. Et moins d'un tour. Sa séquence réduite est donc une répétition $(\overline{T},\overline{T},...,\overline{T})$ de $2n$ $\overline{T}$. Soit $m\geq 2n$ puis $m=2n$. Gagné !

Le nombre d'étapes est $2n$ : en termes de complexité, notre première idée était la bonne. Elle n'était pas unique. D'autres « chorégraphies » terminent aussi en $2n$ étapes. Voyez-vous comment ?