Une épiphanie des mathématiques !
En citant les suites définies par une relation récurrente du type $$ u_{n+1} = f(u_n) $$ où $f$ applique continûment un intervalle $I$ de $\mathbb{R}$ dans lui-même, le programme d'enseignement de spécialité de mathématiques de terminale 1 ouvre un horizon autorisant en classe une incursion dans l'univers fascinant du chaos 2345. C'est dans cet esprit que ce texte s'inscrit, s'appuyant d'ailleurs sur un énoncé national d'Olympiades de première 6 que nous étofferons pour le rattacher, in fine, à la célèbre suite logistique 78. Les deux premières parties ne comportent pas de difficulté ; les deux suivantes en appellent à la représentation des nombres en binaire et donc à quelques connaissances propres à la spécialité Numérique et Sciences Informatiques (NSI) de première 9, qui seront néanmoins rappelées. Elles nécessitent aussi davantage d'abstraction : nous privilégierons alors des approches intuitives, en concédant parfois sur la rigueur. L'ensemble pourra servir de guide aux élèves en tant que ressource d'approfondissement ou matière, parmi d'autres, à la préparation de leur Grand oral, en dialogue avec leurs professeurs.
Attention, après cette lecture vous ne malaxerez plus jamais votre pâte à pain, à tarte, à pizza, à galette ou à brioche comme avant !
Transformation $T$ du boulanger et cas d'école
Le geste du boulanger : un premier modèle
Observons à l'œuvre un boulanger du siècle dernier 10. À notre intention, il aura préalablement glissé une fève dans le pâton. Longiligne et de la forme d'une baguette, la pâte est identifiée au segment $[0,1]$. Pour la pétrir on la replie sur elle-même, en son milieu, puis on l'étale uniformément jusqu'à lui rendre sa dimension d'origine (l'unité), et on recommence l'opération plusieurs fois de suite, Figure 1. Il existe d'autres modèles mathématiques pour décrire ces actions — et nous en étudierons un autre (unidimensionnel également) un peu plus loin, mais celui-ci demeure le plus simple.
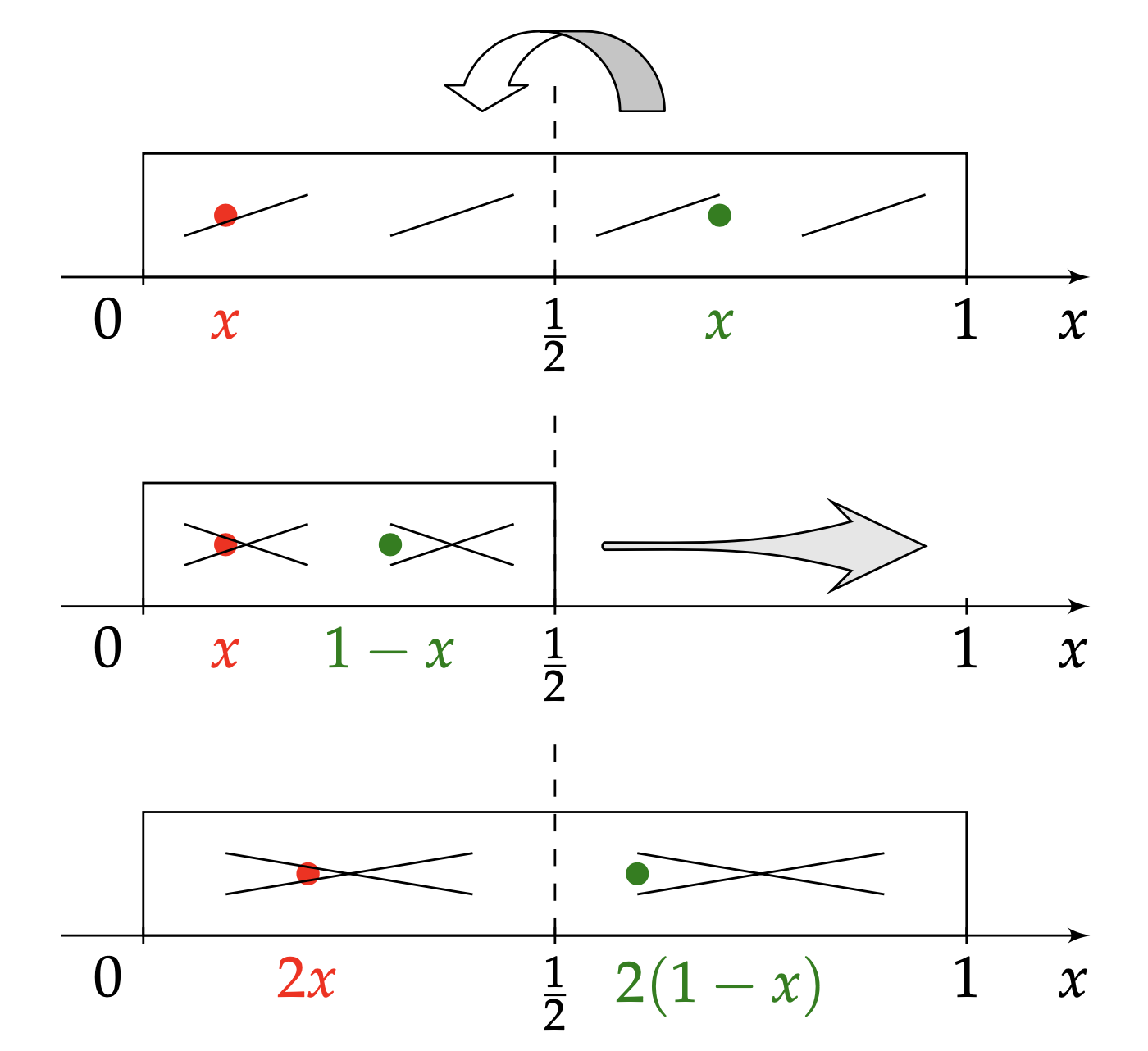
La pâte est repliée sur elle-même en son milieu (voilà pourquoi les stries se croisent) puis uniformément étirée dans le sens de la longueur jusqu’à reprendre sa dimension d’origine. La fève, initialement en l’abscisse $x$, se retrouve en l’abscisse $T(x)$. En rouge : $x \leq \frac1{2}$, en vert : $x \geq \frac12$.
Soit $x$ la position de la fève, supposée ponctuelle, au début d'une opération de pétrissage. De deux choses l'une :
- La fève se situe dans la première moitié de la pâte, soit $0\leq x \leq \frac{1}{2}$. Elle reste insensible au pliage. Mais la dilatation la porte de l'abscisse $x$ à son double, $2x$.
- La fève se situe dans la seconde moitié de la pâte, soit $\frac{1}{2}\leq x \leq 1$. Le pliage l'amène en $1-x$, symétrique de $x$ par rapport à $\frac{1}{2}$. Puis la dilatation en $2(1-x)$.
La transformation $T$ qui à l'abscisse $x\in [0,1]$ de la fève associe son abscisse $T(x)$ à l'issue d'une opération de pétrissage a donc pour expression $$ x \longrightarrow T(x)=\left\{ \begin{aligned} &2x \text{ si }0\leq x \leq \frac{1}{2}\\ &2-2x \text{ si }\frac{1}{2}\leq x \leq 1 \end{aligned} \right. \;\;. $$ Cette application continue raccorde deux portions affines, et son graphe prend la forme d'une « tente » — d'où le symbole $T$ qui en emprunte l'initiale, Figure 2.
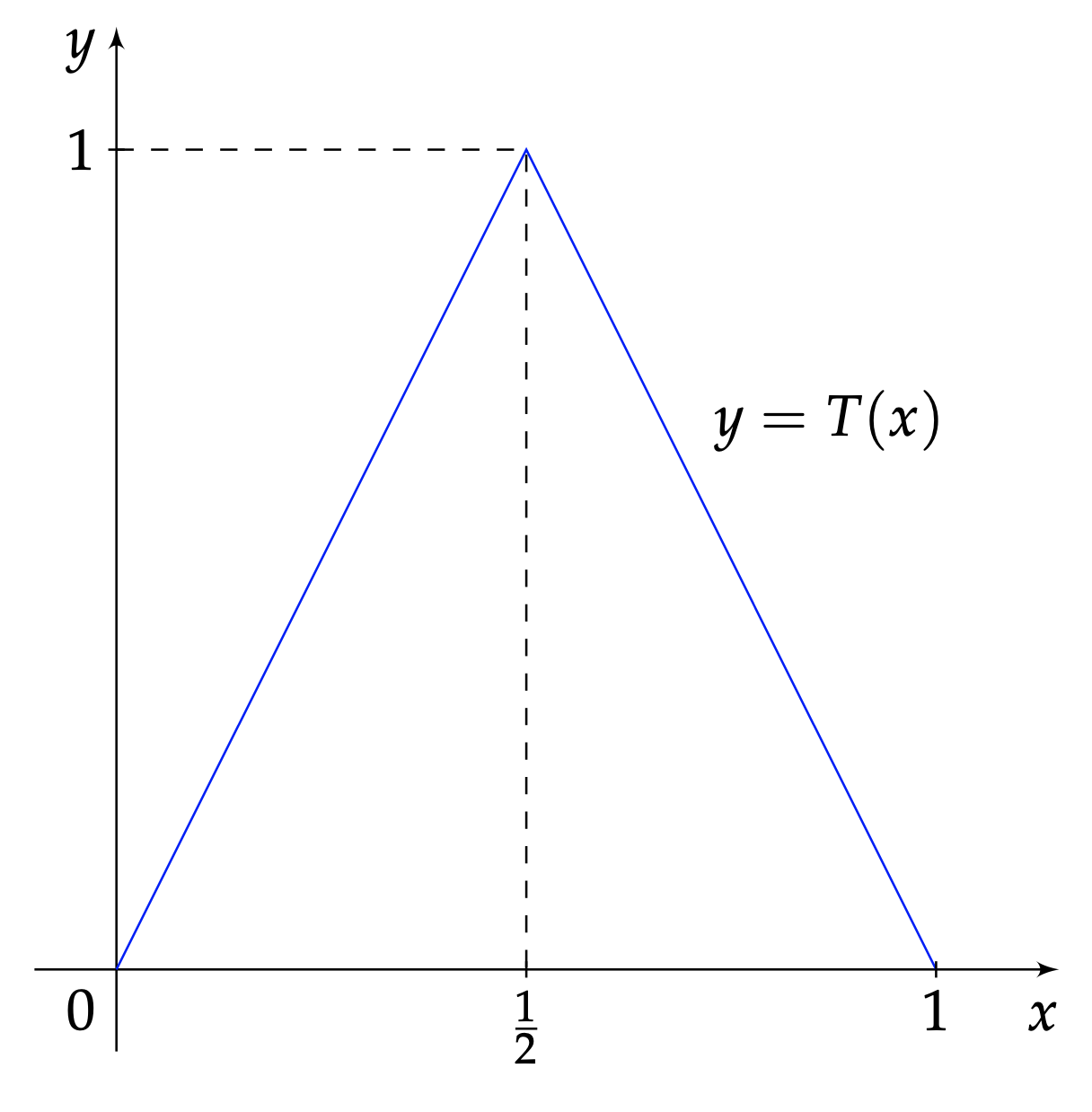
La continuité de $T$ nous conforte dans le cadre des programmes scolaires, dont nous ne nous distancierons qu’en toute fin d’article.
Quelques cas d'école
Dans la droite ligne du paragraphe précédent, intéressons-nous à la suite $(x_n)$ définie par son premier terme $x_0\in[0,1]$ et la relation récurrente, valable pour tout entier $n\geq 0$, \begin{equation} \label{recurrence} x_{n+1} = T(x_n). \end{equation} On retrace ainsi les abscisses successives qu'occupe la fève. Certains points de départ $x_0$ conduisent, après un certain nombre d'itérations, à l'abscisse nulle dont il est ensuite impossible de s'extraire. C'est évidemment le cas de $x_0 = 0$, mais aussi de $x_0 = 1$ (en un coup), de $ x_0 = \frac{1}{2}$ (en deux coups), de $x_0 = \frac{1}{4}$ ou $x_0 = \frac{3}{4}$ (en trois coups), etc. En fait,
Proposition
Tous les nombres dyadiques du segment $[0,1]$, à savoir de la forme $$ x_0 = \frac{p}{2^q} $$ où $q\in\mathbb{N}$ et $p\in\mathbb{N}$ avec $0\leq p \leq 2^q$, conduisent après un nombre fini d'opérations, à l'abscisse nulle.
Démonstration. Quand $q=0$, soit $2^q=1$, le résultat s'impose puisque $p=0$ ou $p=1$, et donc $x_0=0$ ou $x_0 = 1$ qui mènent illico à $x_1=0$. Et tant que $q\geq 1$, appliquer $T$ diminue d'au moins une unité l'exponentiation du $2$ au dénominateur. D'où le résultat. ▢
Les nombres dyadiques ne sont pas les seuls à être le siège d'une suite stationnaire : $x_0 = \frac{1}{3}$, qui via $T$ se fixe en $x_1 = \frac{2}{3}$, l'est aussi. Donc également ses antécédents par $T$, à savoir $\frac{1}{6}$ et $\frac{5}{6}$, les antécédents de ses antécédents, ou les antécédents des antécédents de ses antécédents : on peut en remonter la généalogie à des degrés de plus en plus lointains, tous aboutissent inexorablement à $\frac{2}{3}$ et s'y stabilisent après des applications répétées de $T$.
Plus largement, on remarque aussi l'apparition de cycles. C'est-à-dire qu'après un certain temps la fève reproduit toujours le même parcours en revenant sur ses pas. Ainsi, de $x_0 = \frac{1}{7}$ découlent $x_1 = \frac{2}{7}$, $x_2=\frac{4}{7}$, $x_3=\frac{6}{7}$ qui boucle sur $x_4=\frac{2}{7}=x_2$. Nous venons de mettre à jour une période $3$. Avec un peu de persévérance, on découvrirait des périodes $4$, des périodes $5$, et même des période de toute taille.
Nous comprendrons mieux tout à l'heure d'où proviennent ces exemples. Mais avant, penchons-nous sur un autre phénomène propre au chaos : l'effet papillon 11. Le moindre écart à une valeur initiale $x_0$ ou le plus infime arrondi machine (calculatrice, ordinateur) peuvent tout fausser, parfois de manière difficilement prévisible. L'intervention du hasard est ici contre-intuitive en cela que l'algorithme du boulanger est tout sauf aléatoire, répondant à un protocole on ne peut plus déterministe. Pour en prendre la mesure, initialisons le calcul des termes de la suite $(x_n)$ à la valeur $x_0 = \frac{2}{7}$. Immanquablement, un programme informatique (naïvement conçu) comme celui ci-après la remplace par une valeur approchée, certes extrêmement précise.
#################
#Transformation T
#################
def T(x):
if (x <= 1/2):
return 2*x
else:
return 2 - 2*x
################################
#Calcul d'une centaine de termes
################################
x_0 = 1/7
liste = [0]*101
liste[0] = x_0
for i in range(100):
liste[i+1] = T(liste[i])
######################################################
#Affichage de quelques periodes (qui n'en sont plus !)
######################################################
print(liste[1:4])
print(liste[7:10])
print(liste[52:55])
print(liste[55:58])
Le script produit l'affichage :
[0.2857142857142857, 0.5714285714285714, 0.8571428571428572]
[0.2857142857142847, 0.5714285714285694, 0.8571428571428612]
[0.25, 0.5, 1.0]
[0.0, 0.0, 0.0]
Tout dévie petit à petit : les erreurs s'accentuent puis divergent. En lieu d'un $3$-cycle, nous constatons progressivement se former un escargot (par reports sur la première bissectrice, termes $x_0$, $x_1$,..., $x_9$), avant que ne s'amorce un mouvement d'abord erratique, Figure 3. Fatalement, les calculs viennent mourir sur l'abscisse nulle (termes $x_{52}$, $x_{53}$, $x_{54}$). Sauf raffinement, les nombres sont en effet représentés en machine par leur approximation dyadique. Leur destin est donc couru d'avance comme le présageait la proposition 1.

Un écart infime de $x_0$ à sa valeur nominale (ici dû aux arrondis machines), $\frac27$, engendre un comportement très différent de celui qui était théoriquement attendu (ici, un $3$-cycle).
Pour mieux analyser les forces en jeu, nous devons considérer une seconde transformation du boulanger, laquelle se substituera en partie à la précédente.
Transformation $S$ du boulanger
Une transformation alternative
Cette fois, le boulanger sectionne la pâte en son milieu, rapporte la seconde moitié sur la première par translation, puis agrège le tout avant de l'étirer pour lui rendre sa taille unité, Figure 4.
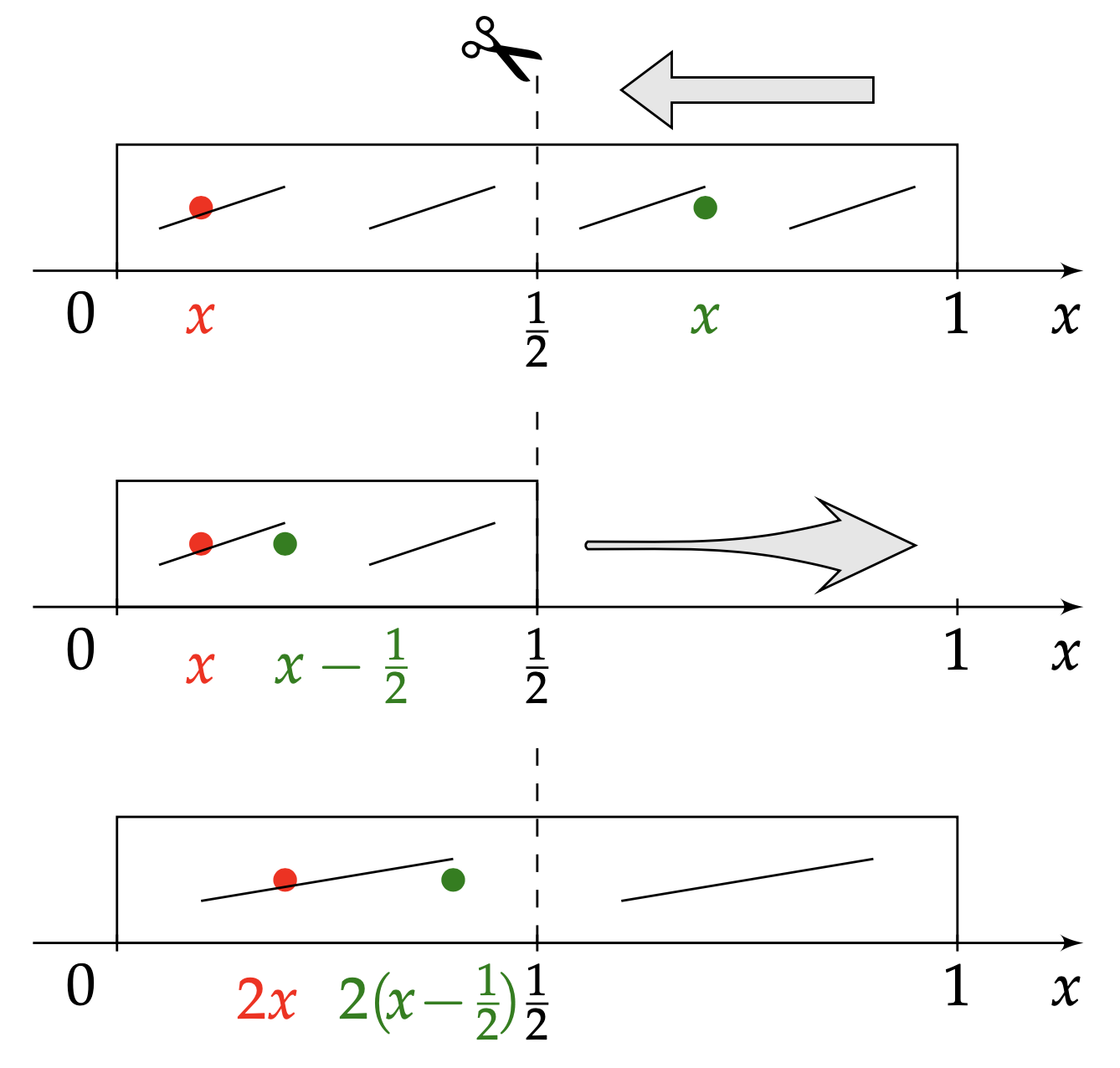
La pâte est coupée en son milieu, la moitié de droite déplacée et amalgamée à celle de gauche, et l’ensemble est étiré dans le sens de la longueur jusqu’à reprendre sa dimension d’origine. La fève, initialement en l’abscisse $x$, se retrouve en l’abscisse $S(x)$. En rouge : $x \lt \frac12$, En vert : $x \gt \frac12$.
Soit $x$ la position de la fève au début d'une opération de pétrissage. De deux choses l'une :
- La fève se situe dans la première moitié (strictement) de la pâte, soit $0\leq x \lt \frac{1}{2}$. Elle est indifférente à la découpe. Mais la dilatation la porte de l'abscisse $x$ à son double, $2x$.
- La fève se situe dans la seconde moitié (strictement) de la pâte, soit $\frac{1}{2}\lt x \leq 1$. La découpe puis la translation l’amènent en $x − \frac12$, et la dilatation en $2x − 1$.
La transformation $S$ qui à l'abscisse $x\in [0,1]$ de la fève associe son abscisse $S(x)$ à l'issue d'une opération de pétrissage a donc pour expression $$ x \longrightarrow S(x)=\left\{ \begin{aligned} &2x \text{ si }0\leq x < \frac{1}{2}\\ &2x-1 \text{ si }\frac{1}{2}< x \leq 1 \end{aligned} \right. \;\;. $$ Le sort de l'abscisse $x=\frac{1}{2}$ n'est pas nettement tranché. Quelle que soit la valeur assignée à $S$ en $\frac{1}{2}$, $S$ y sera discontinue. Convenons par exemple de ce que $$ S\left(\frac{1}{2}\right)=0. $$ L'application $S$ enchaîne ainsi deux portions affines ; son graphe affiche deux stries parallèles comme deux dents de « scie » — d'où le symbole $S$ qui en emprunte l'initiale, Figure 5.
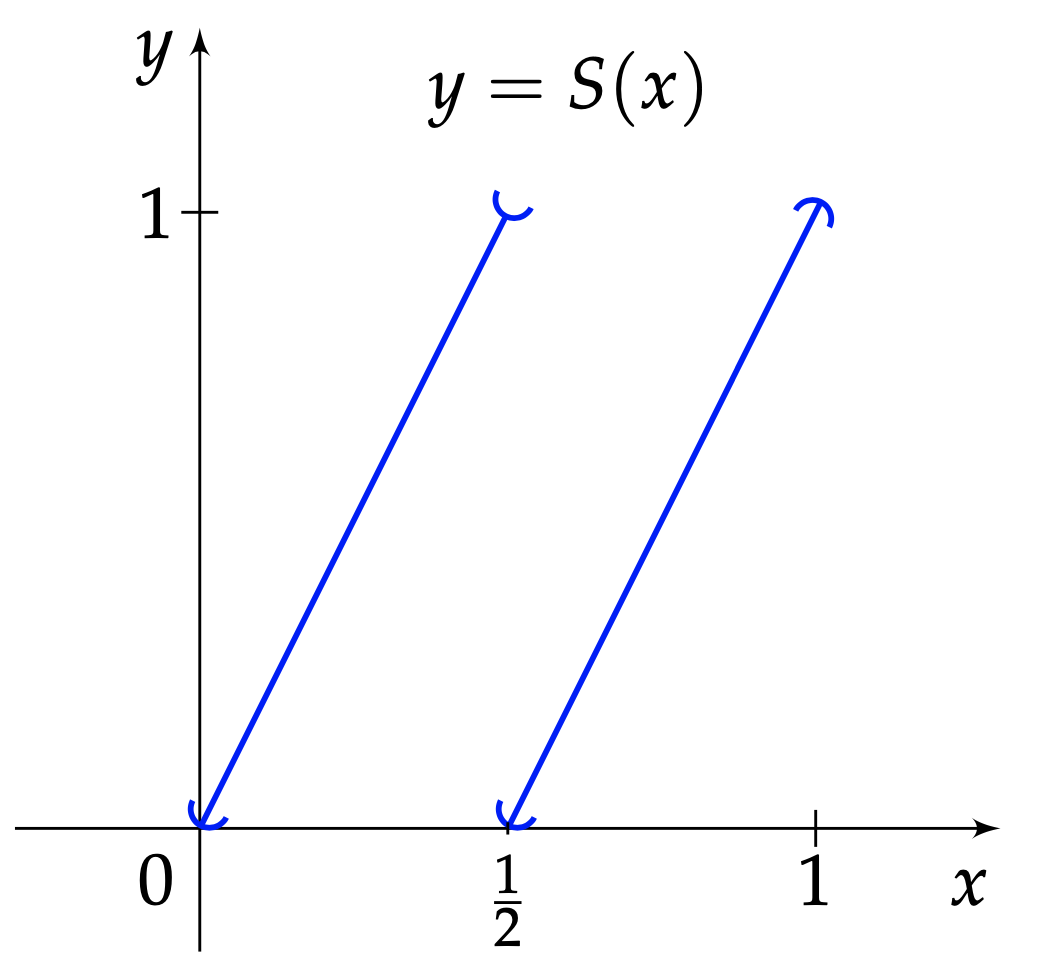
Sur cette version, $S$ est continue à gauche en $\frac12$.
Un autre choix raisonnable eût été de poser $$ S\left(\frac{1}{2}\right)=1, $$ ce qui rendait $S$ continue à gauche en $\frac{1}{2}$ plutôt qu'à droite. Quoi qu'il en soit, on ne devine pas encore à ce stade ce qui lie la nouvelle transformation du boulanger, $S$, à l'ancienne, $T$. Il est temps d'éclaircir ce point.
Principe de substitution et corollaire
Une suite définie par la relation (\ref{recurrence}) vérifie $x_1 = T(x_0)$, $x_2 = T(x_1)=T^2(x_0)$ (où le carré désigne la composée de $T$ par elle-même), $x_3 = T(x_3)=T^3(x_0)$ (où $T^3$ est définie à l'avenant), et plus généralement \begin{equation}\label{xn} x_n = T^n(x_0) \end{equation} où $n\in\mathbb{N}$. La propriété dite de substitution va remplacer les $n$ composées de $T$ par $n-1$ composées de $S$. Énonçons d'abord la
Proposition
On a $T\circ T = T\circ S$, ce qu'on écrit aussi abréviativement : $$ T^2 = TS. $$
Démonstration. Soit $x\in [0,1]$. De deux choses l'une :
- L'abscisse $x$ est située dans la première moitié (strictement) du segment $[0,1]$, soit $0\leq x <\frac{1}{2}$. Dès lors $T(x) = S(x)$, donc $T(T(x))= T(S(x))$.
- L'abscisse $x$ est située dans la seconde moitié (strictement) du segment $[0,1]$, soit $\frac{1}{2}\lt x \leq 1$. Dès lors $S(x)=2x-1$, tandis que $T(x)=2-2x$. Les nombres $S(x)$ et $T(x)$ sont symétriques par rapport à l'abscisse $\frac{1}{2}$. Par symétrie de la fonction « tente », $T$, nous aurons bien $T(T(x))=T(S(x))$.
Il subsiste une incertitude en $x=\frac{1}{2}$. Si nous optons pour $S(\frac{1}{2})=0$, $T(S(\frac{1}{2}))=T(0)=0$, et si nous optons pour $S(\frac{1}{2})=1$, $T(S(\frac{1}{2}))=T(1)=0$. Dans les deux cas, $T^2(\frac{1}{2}) = TS(\frac{1}{2})$. ▢
D'où le
Corollaire
Pour tout entier $n\geq 1$, $T^n=T\circ S^{n-1}$, ce qu'on écrit aussi abréviativement : $$ T^n=TS^{n-1}.$$
Démonstration. La propriété est acquise si $n=1$ puisque $S^0=\mathrm{Id}$. Elle s'étend du rang $n\geq 1$ au suivant par récurrence car \begin{align*} T^{n+1}=T\circ T^n &=T\circ TS^{n-1}\text{ d'après l'hypothèse au rang } n\\ &=(T\circ T)\circ S^{n-1} = T^2\circ S^{n-1} = TS\circ S^{n-1}\\ &\qquad\qquad\quad \text{ grâce au principe de substitution.} \end{align*} Ainsi, $$ T^{n+1}=TS^{n}. $$ ▢
À l'appui de cette dernière proposition, (\ref{xn}) devient \begin{equation} \label{xnprime} x_n = TS^{n-1}(x_0) \end{equation} où $n\in \mathbb{N}^*$. Le bénéfice de cette reformulation proviendra de la commodité à traduire $S$ et ses itérées en base $2$. Ceci est l'objet de la partie suivante.
Étude de la transformation $S$
Calculs en binaire
De la base $10$ à la base $2$
Tout nombre réel possède un développement décimal. Ainsi, $\pi = 3,1415926\cdots$. Certains nombres, dits décimaux, en possèdent un qui a la particularité d'être fini (c'est-à-dire prolongeable par une traîne illimitée de $0$) : par exemple $\frac{1}{5} = 0,2$. Auquel cas, ils en admettent un autre, infini : ainsi la fraction $\frac{1}{5}$ s'écrit-elle aussi $0,1999\cdots$ ou encore $0,1\overline{9}$ pour marquer la répétition du motif $9$ ; cela tient à ce que la somme géométrique $$ \frac{9}{10}+\left(\frac{9}{10}\right)^2+\left(\frac{9}{10}\right)^3+\ldots $$ vaut l'unité 1213.
De la même manière, tout réel possède un développement dyadique, à savoir en base $2$ et non plus $10$. Les nombres dits dyadiques sont ceux qui en possèdent un fini : par exemple $0,101_2$ n'est autre que $\frac{1}{2}+\frac{0}{4}+\frac{1}{8}$, soit $\frac{5}{8}$. Auquel cas, ils en admettent un autre, infini : ainsi la fraction $\frac{5}{8}$ s'écrit-elle aussi $0,100\overline{1}_2$ ; cela tient à ce que la somme géométrique $$ \frac{1}{2}+\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3+\ldots $$ vaut l'unité. Il faut parfois savoir jongler entre ces deux développements : cela nous servira dans la suite. Signalons enfin que les nombres dyadiques sont particulièrement importants pour le rôle qu'ils jouent en informatique. Par ailleurs, notons que les indices « $2$ » ajoutés au bout des développements $0,101_2$ et $0,100\overline{1}_2$ rappellent que la base $2$ nous sert de cadre. Sauf ambiguïté, nous les omettrons volontiers.
Il se trouve que $S$ opère aisément en base $2$. Pour l'apprécier, choisissons un réel $x\in [0,1]$ et représentons-le par son développement dyadique14 \begin{equation} \label{representationbinaire} x = 0,d_1 d_2 d_3 d_4 ... \end{equation} Distinguons essentiellement deux cas :
- Si $0\leq x <\frac{1}{2}$, alors $d_1 = 0$. Faire agir $S$ sur $x$ décale en bloc et vers la gauche ses digits $d_1=0$, $d_2$, $d_3$,$\ldots$ Donc $$ S(x) = 0,d_2 d_3 d_4 \cdots $$
- Si $\frac{1}{2}\lt x\leq 1$, alors $d_1 =1$. Doubler $x$ décale en bloc et vers la gauche ses digits, soit $2x=1,d_2 d_3 d_4 \cdots$. En soustrayant $1$, il reste à nouveau $$ S(x) = 0,d_2 d_3 d_4 \cdots $$
Tout se passe comme si $S$ imprimait un simple décalage à gauche des digits, avec effacement de l'unité. Les mathématiciens y voient là un argument supplémentaire au choix du symbole $S$ désignant la transformation, en référence à l'initiale du mot (anglais) shift. Il reste cependant un détail à régler, l'image par $S$ de $\frac{1}{2}$. Selon que $\frac{1}{2}$ est représenté par $0,1\overline{0}$ ou $0,0\overline{1}$, le décalage suivi de l'effacement débouche sur $0$ ou sur $1$ et correspond donc à la version continue à gauche ou continue à droite de $S$.
Du binaire au chaos
Visuellement, les points $x_0$ qui initient un $p$-cycle pour $S$ ressortent aussitôt. Choisissons comme point de départ $$ x_0 = 0,d_1 d_2 \cdots d_k \overline{d_{k+1} d_{k+2} \cdots d_{k+p}}, $$ où le motif surligné se répète à l'infini ($x_0$ est de ce fait un nombre rationnel, 15). La suite récurrente associée vérifiant pour tout $n\geq 0$ \begin{equation} x_{n+1} = S(x_n) \label{recurrence2} \end{equation} embraye en effet, après un régime transitoire constitué de $k$ itérations, sur un engrenage de période $p$. En toute transparence, il faut ici pointer une discrète subtilité. Ainsi, $x_0 = 0,d_1 d_2 \cdots d_k \overline{0101}$ est-il à l'origine d'un $4$-cycle dont la période, au sens de la plus petite qui soit, n'est que de $2$ ; la faute incombe à la séquence « $01$ », redondante dans le motif dyadique. On ne peut donc pas laisser complètement libres les choix des digits $d_{k+1}$, $d_{k+2}$, $\ldots$, $d_{k+p}$, mais la marge est cependant grande. Par exemple, quand $p\geq 2$, fixer l'extrémité gauche $d_{k+1}$ à $1$ et les digits suivants $d_{k+2}$,$\ldots$, $d_{k+p}$ à $0$ offre une solution satisfaisante.
Enfin, l'« hypersensibilité » de la suite $(x_n)$ à la donnée initiale $x_0$ affleure clairement. Si $$ x_0 = 0,d_1 d_2 \cdots d_k d_{k+1} \cdots, $$ partir du point très voisin16 $$ x'_0 = 0,d_1 d_2 \cdots d_k \overline{d'_{k+1} d'_{k+2} \cdots d'_{k+p}} $$ engage dans un $p$-cycle, qui n'a, a priori, plus rien à voir avec le comportement de la suite gouvernée par $x_0$. En jouant sur $k$ et sur $p$, on rapproche $x'_0$ de $x_0$ et on étend le cycle à loisir.
De $S$ vers $T$, de $T$ vers la suite logistique
De $S$ vers $T$
Rappelons à cet endroit qu'une suite $(x_n)$ définie par son premier terme $x_0 \in [0,1]$ et la propriété de récurrence (\ref{recurrence}) valable pour tout entier $n\geq 0$, $$ x_{n+1} = T(x_n), $$ vérifie les relations (\ref{xn}) et (\ref{xnprime}) : $$ x_n = T^n(x_0)=TS^{n-1}(x_0) $$ dès que $n\geq 1$. Sans surprise, les effets chaotiques des itérées de $S$ vont se répercuter sur celles de $T$. Formalisons cela en deux propositions.
Proposition
Si le premier terme $x_0$ est le siège d'un $p$-cycle pour $S$, il est aussi celui d'un $p$-cycle pour $T$.
Démonstration. Après un certain temps d'attente $k$, nous avons donc $$ S^{k+1}(x_0)=S^{k+p}(x_0). $$ En composant à gauche par $T$, il vient du corollaire 3 $$ T^{k+2}(x_0)=T^{k+p+1}(x_0). $$ Cela signifie qu'un $p$-cycle s'enclenche aussi pour $T$, en léger différé. ▢
Il convient toutefois d'être prudent. Nous avons procédé par implications dans la démonstration ci-dessus. Un $p$-cycle exact pour $S$ fournit un $p$-cycle image pour $T$ dont la période peut s'être réduite, et diviser17 strictement $p$. C'est le cas lorsque \begin{align*} x_0 &= 0,\overline{01}\\ &= \frac{1}{4}+\frac{1}{16}+\frac{1}{64}+...\\ &=\frac{1}{3} \end{align*} qui, en itérant par $T$, génère la suite stationnaire à $\frac{2}{3}$. Il faut donc prendre quelques précautions. Quand $p\geq 3$, on peut fixer l'extrémité gauche $d_{k+1}$ à $1$ et les digits suivants, $d_{k+2},\cdots$ $d_{k+p}$ à $0$. Le cycle pour $S$ parcourt les valeurs \begin{align*} &0,\overline{10...000} ;\\ &0,\overline{00...001} ;\\ &0,\overline{0...0010} ;\\ &\ldots\\ &0,\overline{0100...0}.\\ \end{align*} Tous ces nombres à l'exception du premier se trouvent entre $0$ et $\frac{1}{2}$, dans la portion strictement croissante de la « tente ». Leur diversité est donc préservée par $T$. Si bien que le cycle pour $T$ affiche une période minimale de $p-1$. Mais $p-1$ ne divise pas $p$ puisqu'il dépasse sa moitié. Nécessairement, le cycle image est exactement de période $p$. Ainsi $x_0=0,\overline{100}$ garantirait-il un $3$-cycle exactement pour $T$. Or \begin{align*} x_0 &= 0,\overline{100}\\ &=\frac{1}{2}+\frac{1}{16}+\frac{1}{128}+\ldots\\ &=\frac{4}{7}. \end{align*} Voilà qui est cohérent avec la première partie.
Proposition
La suite $(x_n)$ associée à $T$ est elle aussi « hypersensible » au terme initial $x_0$.
Démonstration. L'idée, que nous ne ferons qu'esquisser, de déformer et de périodiser les décimales de $x_0$ à partir d'un certain rang $k$ opère encore, modulo les réserves exprimées quant au transport de la période par $T$ et que nous avons levées. ▢
De $T$ vers la suite logistique
Les suites logistiques comptent parmi les objets les plus captivants des mathématiques 8. Elles interviennent classiquement en dynamique des populations 18. Nous ramenons dans ce paragraphe l'une d'elles, celle définie par son premier terme $u_0\in [0,1]$ et la relation récurrente valable pour tout entier $n\geq 0$ $$ u_{n+1}=4 u_n (1-u_n) $$ à l'étude d'une suite construite en itérant $T$. Au fond, le lien entre les deux n'est pas si étonnant tant les courbes de $f:x\rightarrow 4x(1-x)$ et de $T$ se ressemblent, Figure 6.
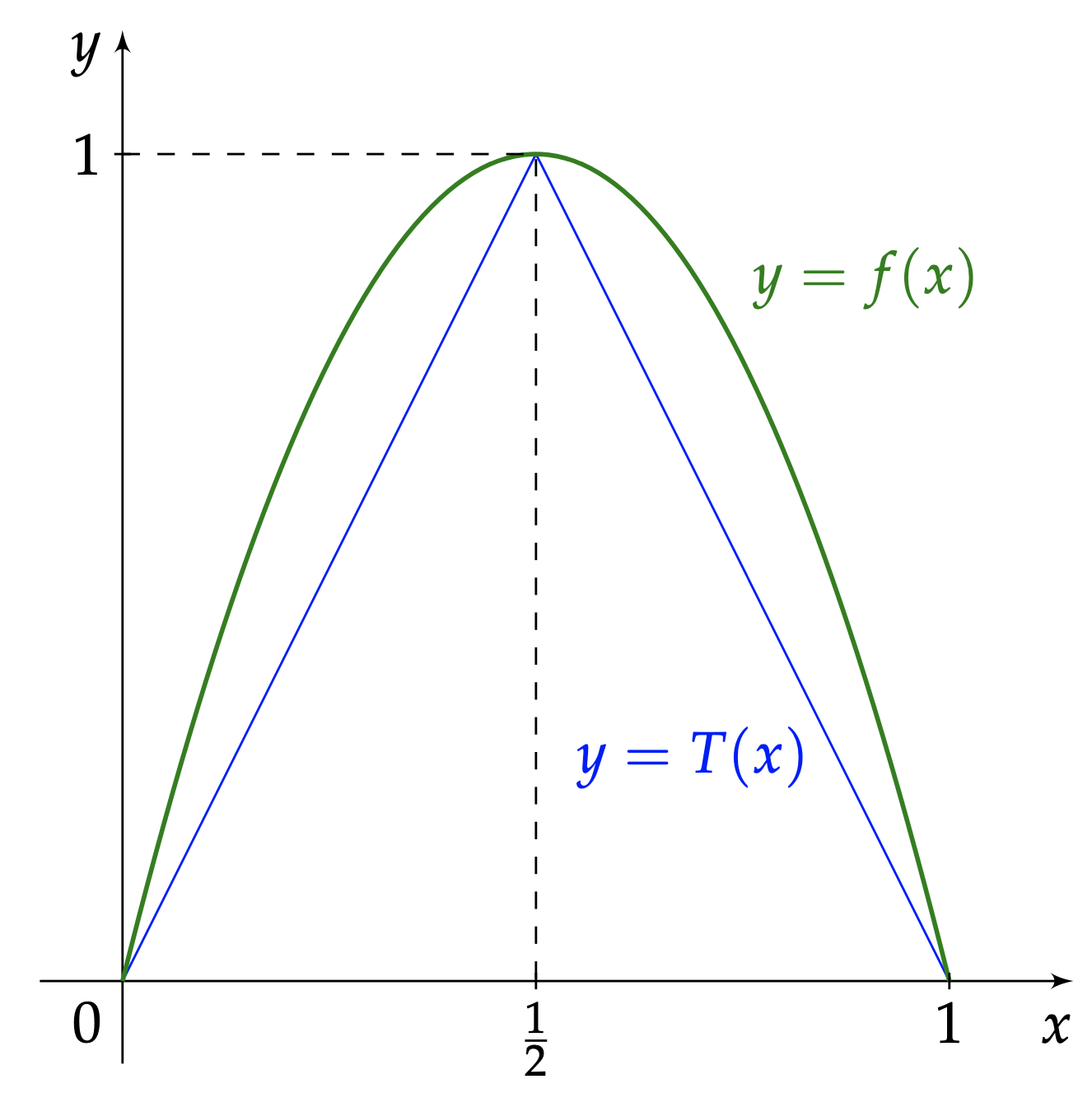
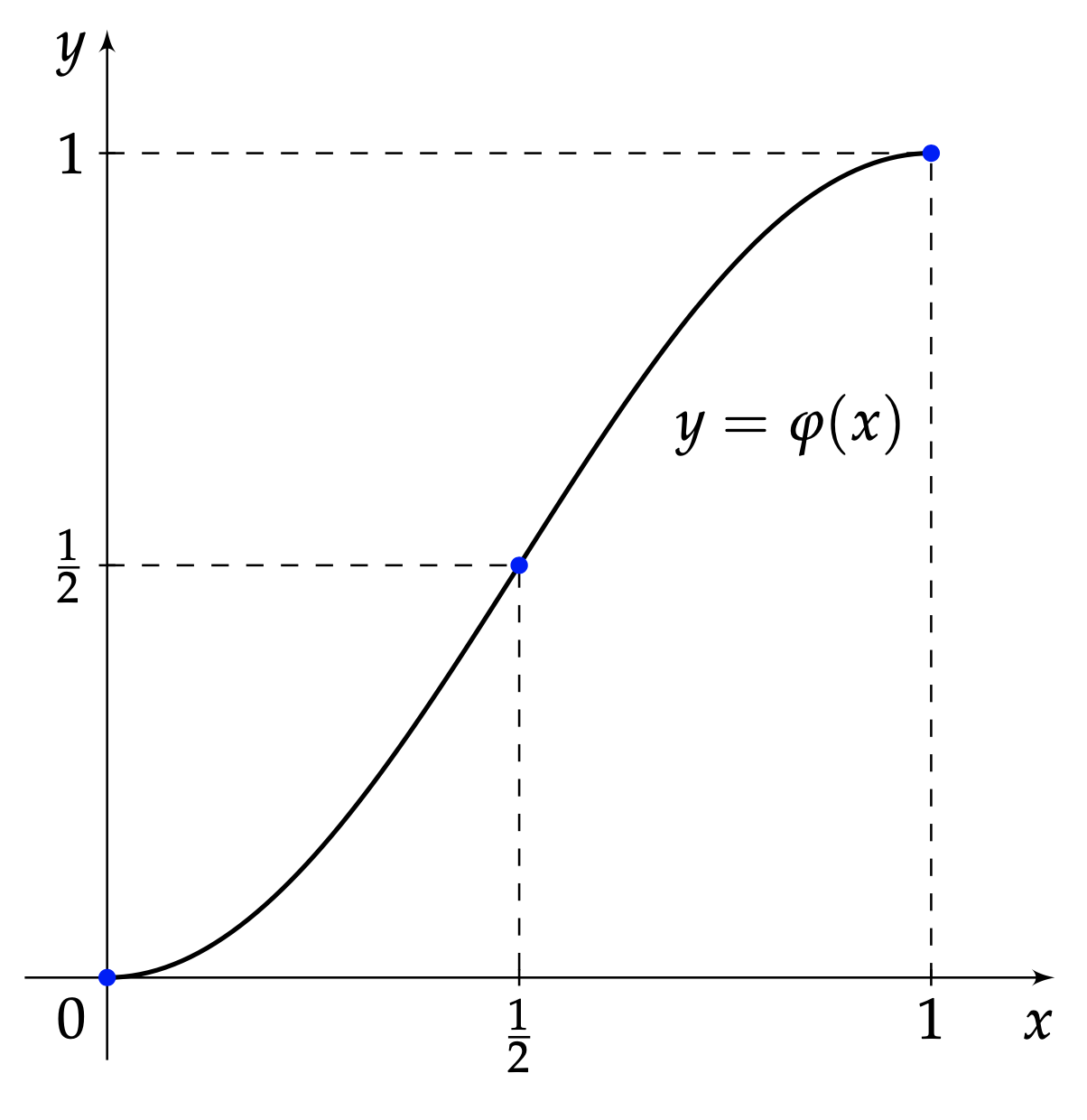
Ce tour de passe-passe tient au changement de variable bijectif $\varphi : [0,1]\rightarrow [0,1]$, $$ x \longrightarrow \varphi(x) = \sin^2(\frac{\pi x}{2}). $$ En effet, puisque $u_0 \in [0,1]$, associons-lui son antécédent par $\varphi$, $x_0$, l'unique réel $x_0 \in [0,1]$ tel que $u_0 = \varphi(x_0)=\sin^2\left(\frac{\pi x_0}{2}\right)$, Figure 7.
Des formules de trigonométrie usuelles 19 on tire \begin{align*} u_1 &= \left(2\sin(\frac{\pi x_0}{2})\cos(\frac{\pi x_0}{2})\right)^2\\ &=\sin^2(\frac{\pi (2x_0)}{2}) \end{align*} De deux choses l'une :
- Lorsque $x_0 \in [0,\frac{1}{2}]$, $2x_0\in[0,1]$ ;
- Lorsque $x_0 \in [\frac{1}{2},1]$, on peut, grâce aux symétries de la fonction sinus, avantageusement remplacer $2x_0$, qui s'échappe du segment $[0,1]$, par $2-2x_0$ qui s'y maintient.
Dans tous les cas, c'est la transformation $T$ que nous invoquons en posant naturellement $x_1 = T(x_0)$, dont dérive $u_1 = \varphi(x_1)$. Plus généralement, $$ u_n = \varphi(x_n) $$ où $x_n =T^n(x_0)$ est la suite récurrente définie par $x_0$ et la relation valable pour tout entier $n\geq 0$, $x_{n+1} = T(x_n)$. Autrement formulé, \begin{equation} u_n = f^n(u_0) = \varphi(T^n(\varphi^{-1}(u_0))). \end{equation} On peut par conséquent s'attendre à ce que la suite logistique hérite du comportement chaotique observé avec $T$.







