Coupez les moteurs... Silence on tourne !
Tournez son volant, votre voiture tourne : cela paraît logique, pourtant... sauriez-vous nous dire de quel rayon ? Et jureriez-vous qu'aucune roue ne dérape ? Plus que de votre confort, il en va de votre tenue de route, donc de votre sécurité. Aussi, dès l'origine les constructeurs automobiles n'ont-ils cessé d'apporter des réponses à ces questions : d'abord à l'aide d'épures géométriques puis, l'informatique aidant, à renfort de simulations numériques et d'outils de conception sur ordinateur. Jouons ici aux ingénieurs en herbe et ouvrons le capot 12. Après avoir considéré le monocycle, le vélo et le tricycle, grâce auxquels nous appréhenderons mieux les lois de la physique à respecter et les défis technologiques à relever, nous étudierons la problématique propre aux quatre-roues. Enfin, nous proposerons quelques pistes d'approfondissement.
Nous mobiliserons des connaissances mathématiques du collège (droites, cercles, rotations, intersections, parallélogrammes, trapèzes) 3 et du lycée (vecteurs, trigonométrie) 4, et manipulerons deux langages de programmation couramment utilisés en classe : Python, à des fins algorithmiques, calculatoires et pédagogiques, et GeoGebra, pour paramétrer, dessiner et animer une chaîne cinématique. Dans l'industrie, des logiciels plus sophistiqués — tel SolidWorks — peuvent également se rencontrer, mais ils ne nous seront pas indispensables.
Sous la houlette de leurs professeurs, et le cas échéant dans un cadre alloué à la cointervention, aux projets interdisciplinaires, au grand oral, etc. ce texte pourra servir aux collégiens, aux élèves des CAP, baccalauréat professionnel ou BTS de la spécialité Maintenance des véhicules 567, aux lycéens de la série STI2D de la voie technologique sur leur spécialité Physique-Chimie — Mathématiques 8 ainsi qu'aux étudiants des classes préparatoires scientifiques.
Il pourra flotter comme un parfum d'enfance ; de balades en vélo, de circuits de petites voitures au matin d'un Noël, ou bien de mobylettes...
Avec une roue
Fixons notre attention sur le mouvement d'une roue. En contact avec le sol, elle décrit une trajectoire, matérialisée par l'empreinte d'un pneu sur un chemin de terre, ou par de la trace de gomme sur une route goudronnée. Plus précisément, nous tiendrons pour acquis ce principe physique, certes plus abstrait mais de bon sens :
Courbure et roulement sans glissement
Quand elle roule sans glisser, bien perpendiculaire au sol, une roue — ou plutôt son centre — décrit un arc assimilable, à chaque instant, à un virage qu'elle vient tangenter et dont le centre instantané $I$ de la courbure se trouve dans le prolongement de l'axe, figure 1.
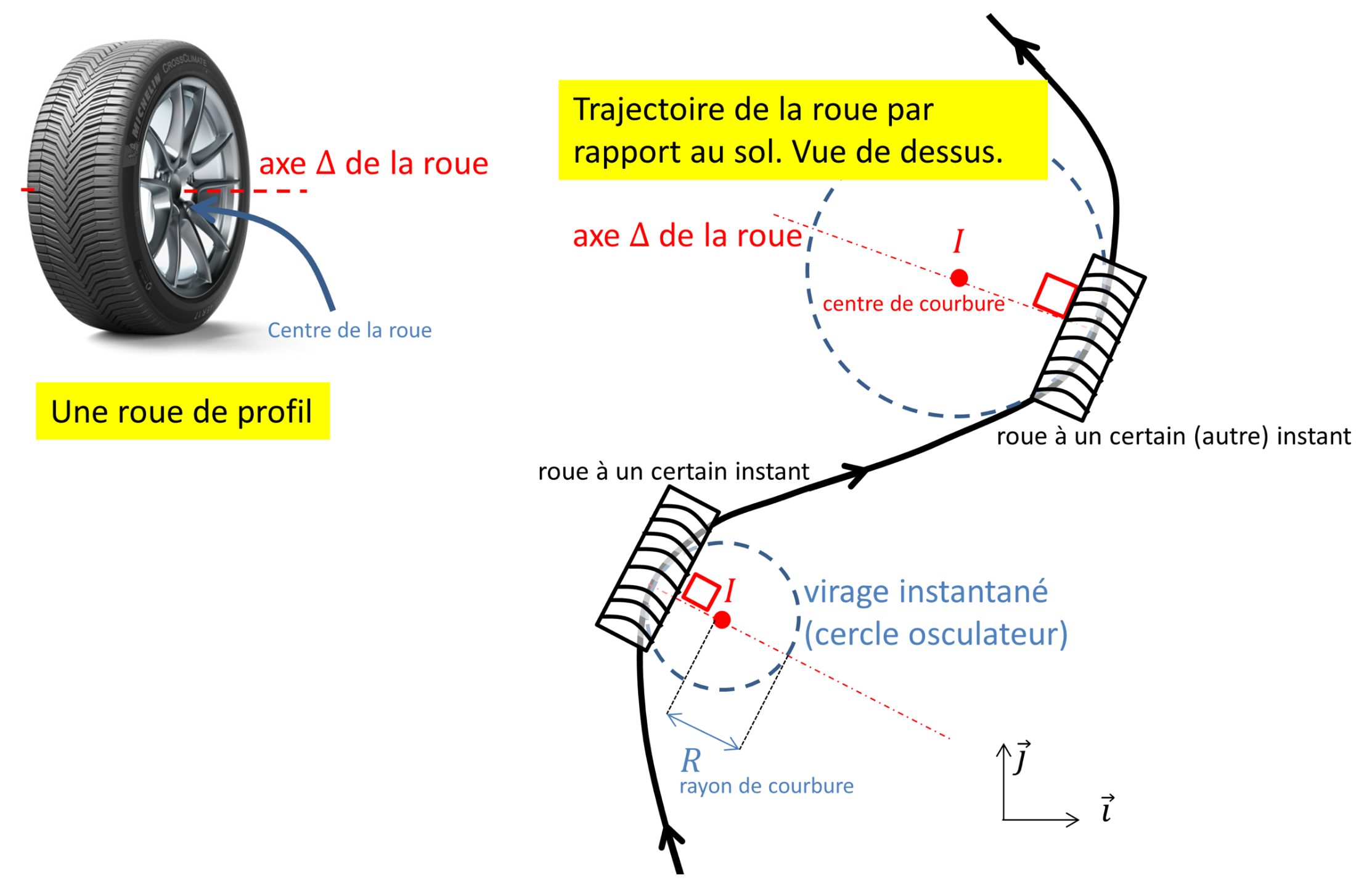
La roue est représentée à deux instants. L'axe $ \Delta$ est normal au mouvement, lequel s'apparente à chaque instant à une portion de cercle, dit osculateur, de centre $I$, dit de courbure ou de rotation. On assimile l'empreinte au sol à une bande infiniment mince, donc à un arc.
Ce tableau est bien sûr idéal, et nous comprendrons progressivement en quoi. Mais appliquons d'ores et déjà son résultat aux deux-roues (vélo, mobylette), ou aux trois-roues (tricycle, fourgon postal, char à voile) avant d'affronter le cas, plus épineux, des véhicules à quatre roues.
Avec deux ou trois roues
Entrer dans un virage en deux-roues
Examinons le vélo représenté en vue de dessus sur la figure 2. Nous y lisons l'entraxe $e$, appelé empattement, ainsi que l'angle de braquage $\alpha$ de la roue avant par rapport au cadre.
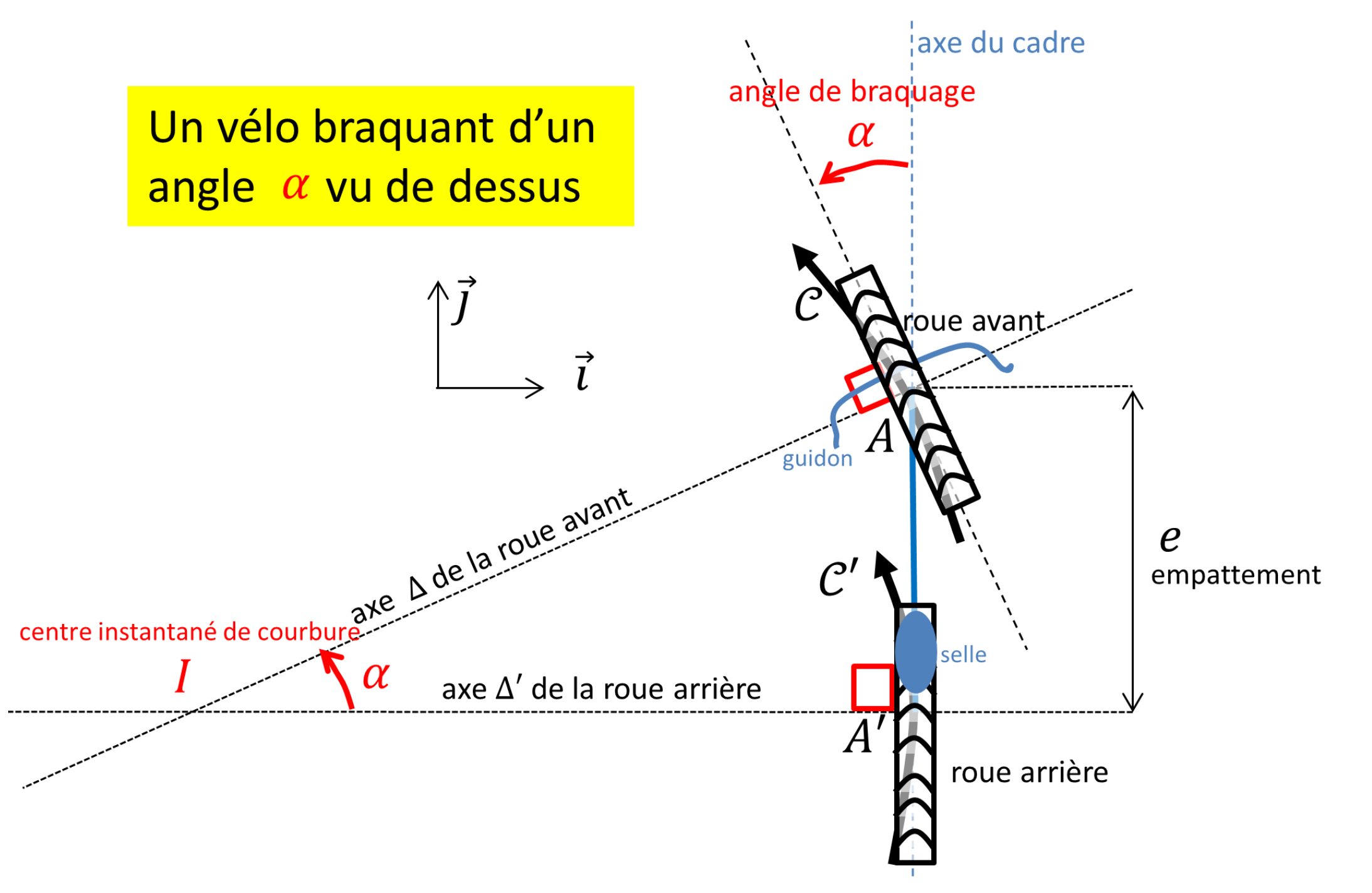
Tant que le vélo ne dérape pas, le centre instantané $I$ de la courbure se trouve à l'intersection des axes $\Delta$ et $\Delta'$. Les roues arrière et avant parcourent les portions de deux cercles concentriques, $\mathcal{C}$ et $\mathcal{C'}$. En décomposant l'angle plat traversant le point $A$, nous recueillons $$ \pi = \alpha + \frac{\pi}{2} + \widehat{IAA'}, $$ donc $$ \widehat{IAA'} = \frac{\pi}{2}-\alpha. $$ Puis dans le triangle $IAA'$, nous calculons $$ \pi = (\frac{\pi}{2}-\alpha) + \frac{\pi}{2} + \widehat{AIA'}, $$ d'où $$ \widehat{AIA'} = \alpha. $$ Dès lors, les rayons $R=IA$ et $R'=IA'$ des cercles instantanés de courbure (dits cercles osculateurs) valent \begin{equation}\label{rayonbicyclette} R = \frac{e}{\sin\alpha}\quad \text{et } \quad R'=\frac{e}{\tan\alpha} \end{equation} En maintenant l'angle de braquage $\alpha$ constant, les roues du vélo suivent, de proche en proche, deux cercles aux rayons fixes et de même centre, tout aussi immobile : on tourne en rond.
Enfin, nous retiendrons de la formule (\ref{rayonbicyclette}) que les rayons $R$ et $R'$ sont proportionnels à l'empattement $e$. Un vélo très court, de type BMX, est donc plus maniable qu'un vélo très long, de type tandem.
L'autostabilité, ou pourquoi le guidon revient tout seul en ligne droite au sortir d'un virage
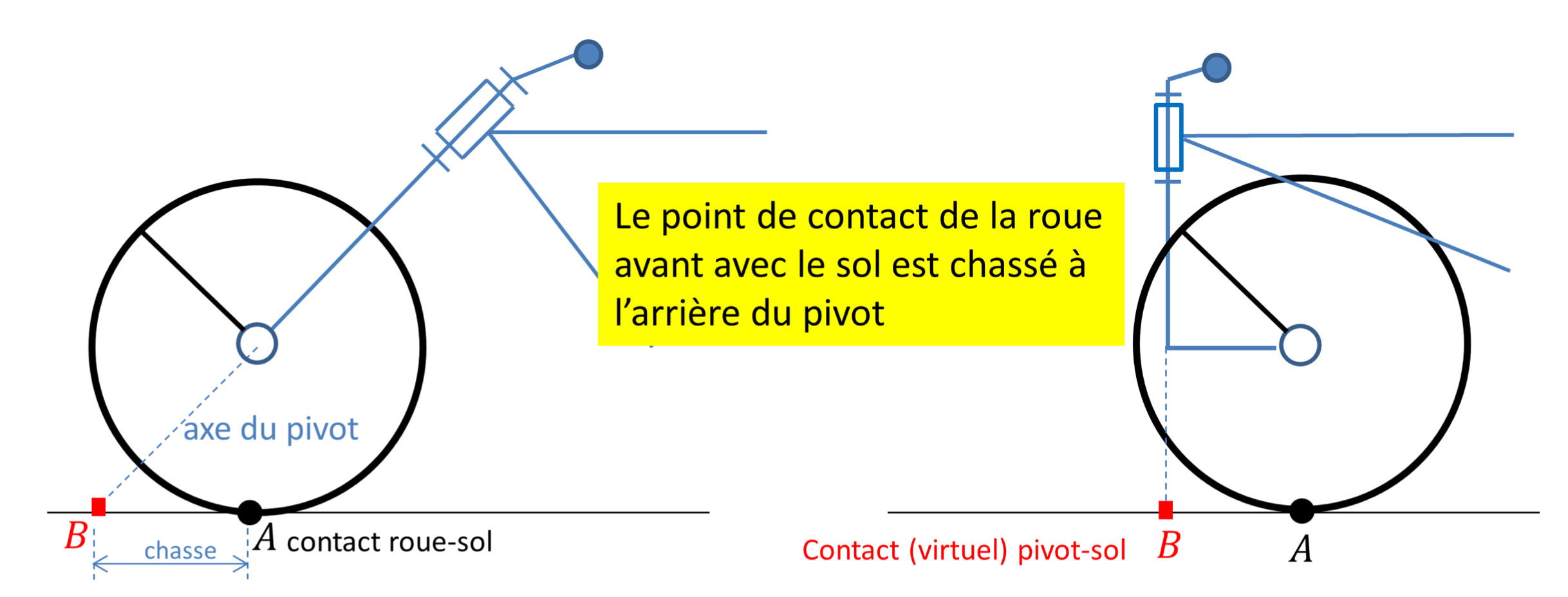
Sur un deux-roues, la fourche avant n'est pas verticale, mais oblique — parfois jusqu'à l'extrême comme en Harley-Davidson. Cela a pour conséquence d'augmenter l'empattement, mais aussi de déporter vers l'arrière de l'axe du guidon le point de contact du pneu avec le sol, figure 3 de gauche. Cet écart permet à la roue de se réaligner naturellement en sortie de virage, retrouvant ainsi sa position la plus neutre. Pour en saisir la raison, il est plus pratique de «redresser» la scène en observant le phénomène, assez similaire, sur une roue de chariot (de type caddie), figure 3 de droite. L'axe du pivot est alors vertical, mais un petit décrochement chasse le point de contact à l'arrière du pivot. Du reste, la roue demeure perpendiculaire au support, quand elle se coucherait si l'axe était incliné, ce qui ajouterait une difficulté de compréhension que nous préférons éclipser.
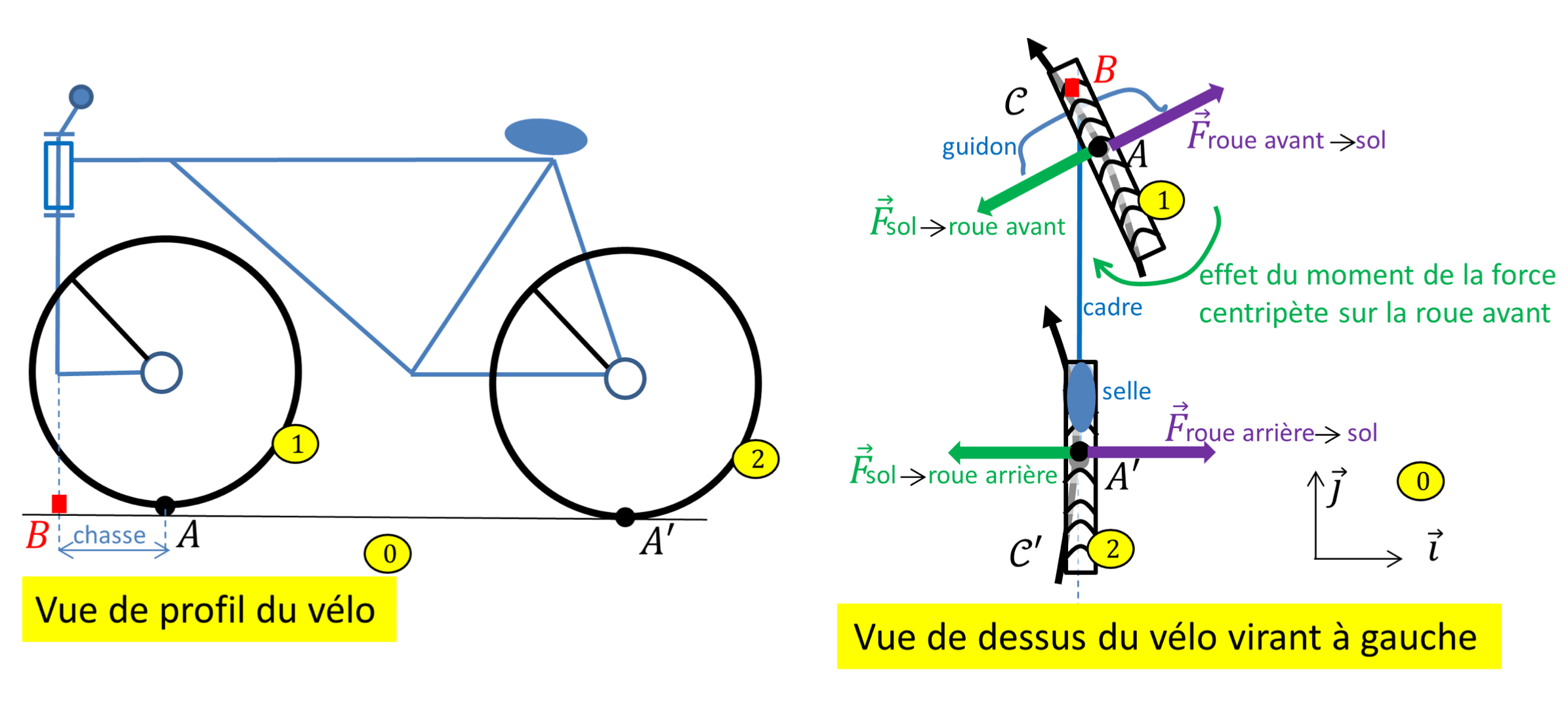
Imaginons donc un vélo équipé, pour simplifier, d'une (grande) roue de caddie devant, figure 4 de gauche. En avançant tout en épousant la courbure, les roues subissent les forces centrifuges $\overrightarrow{F}_{\text{roue avant}\rightarrow\text{sol}}$ et $\overrightarrow{F}_{\text{roue arrière}\rightarrow\text{sol}}$ qui tendent à les exclure du virage, de celle qui plaque un passager sur le conducteur dans un virage à droite 9. Le sol les maintient en leur opposant les forces de frottement10 $\overrightarrow{F}_{\text{sol}\rightarrow\text{roue avant}}$ et $\overrightarrow{F}_{\text{sol}\rightarrow\text{roue arrière}}$ qualifiées de centripètes dans ce contexte. Mieux, la première rappelle la roue avant dans la direction du cadre grâce au moment qu'elle exerce par rapport au pivot, un peu comme elle claquerait une porte, figure 4 de droite. La seconde n'a pas cet effet sur la roue arrière, plus rigide. En lâchant le volant, un deux-roues reprend ainsi spontanément sa trajectoire rectiligne : c'est astucieux11... et rassurant !
Et maintenant, une virée en trois-roues !
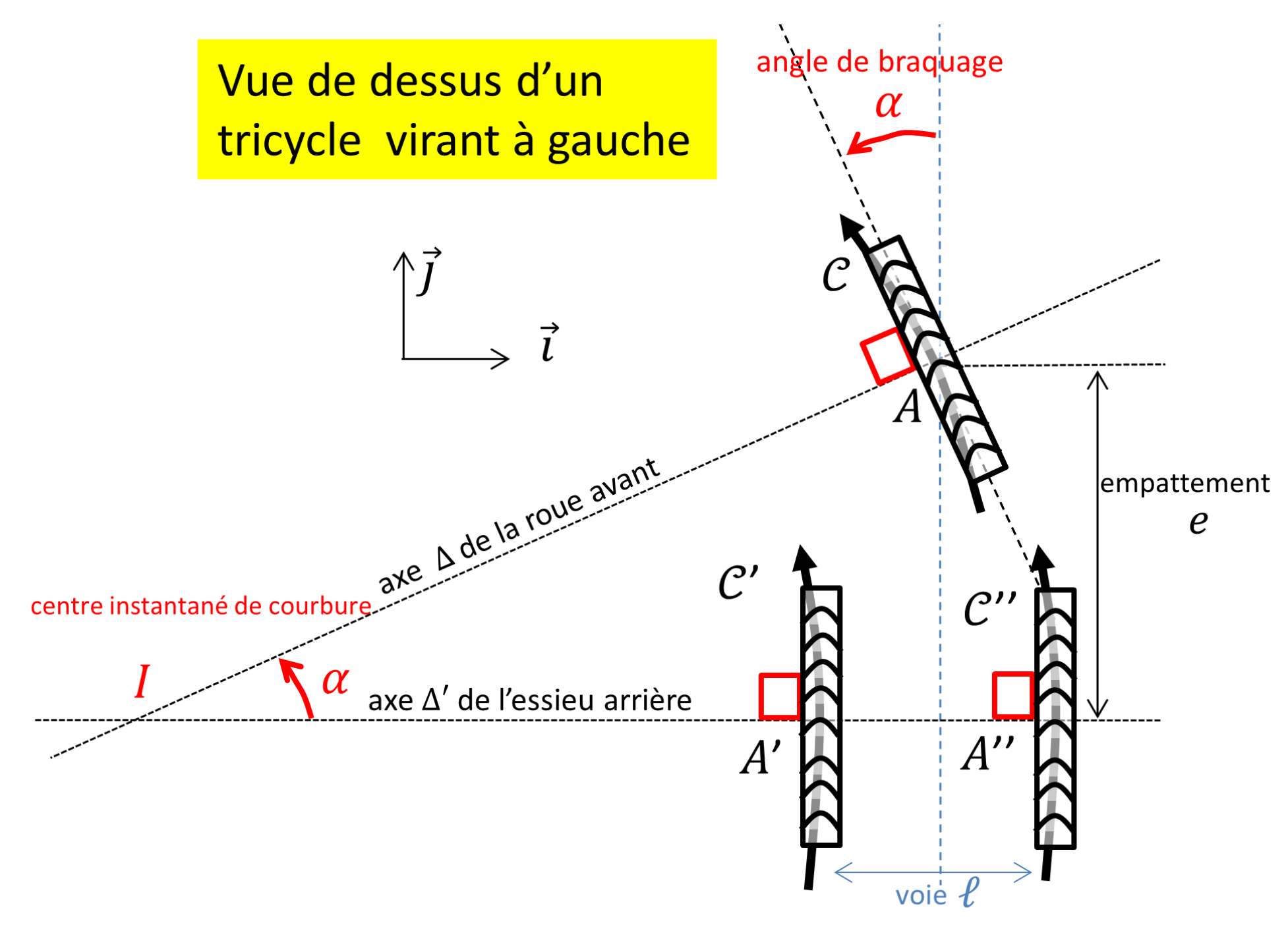
La description faite pour le deux-roues s'étend aux trois-roues qui possèdent une roue mobile (pivotante) à l'avant et deux roues non pivotantes à l'arrière12. Notons $\ell$ la largeur de l'essieu, ou voie. Le guidon est situé dans l'axe médian du véhicule, figure 5. Braquons-le d'un angle $\alpha$. Les trois roues tournent ensemble de la rotation de centre (commun) $I$, distant des rayons respectifs \begin{equation}\label{troisroues} R = \frac{e}{\sin\alpha},\quad R'_1=\frac{e}{\tan\alpha}- \frac{\ell}{2}\quad \text{et}\quad R'_2=\frac{e}{\tan\alpha}+\frac{\ell}{2} \end{equation}
Avec quatre roues
C'est avec quatre roues que les choses se corsent.
Où est le problème ?
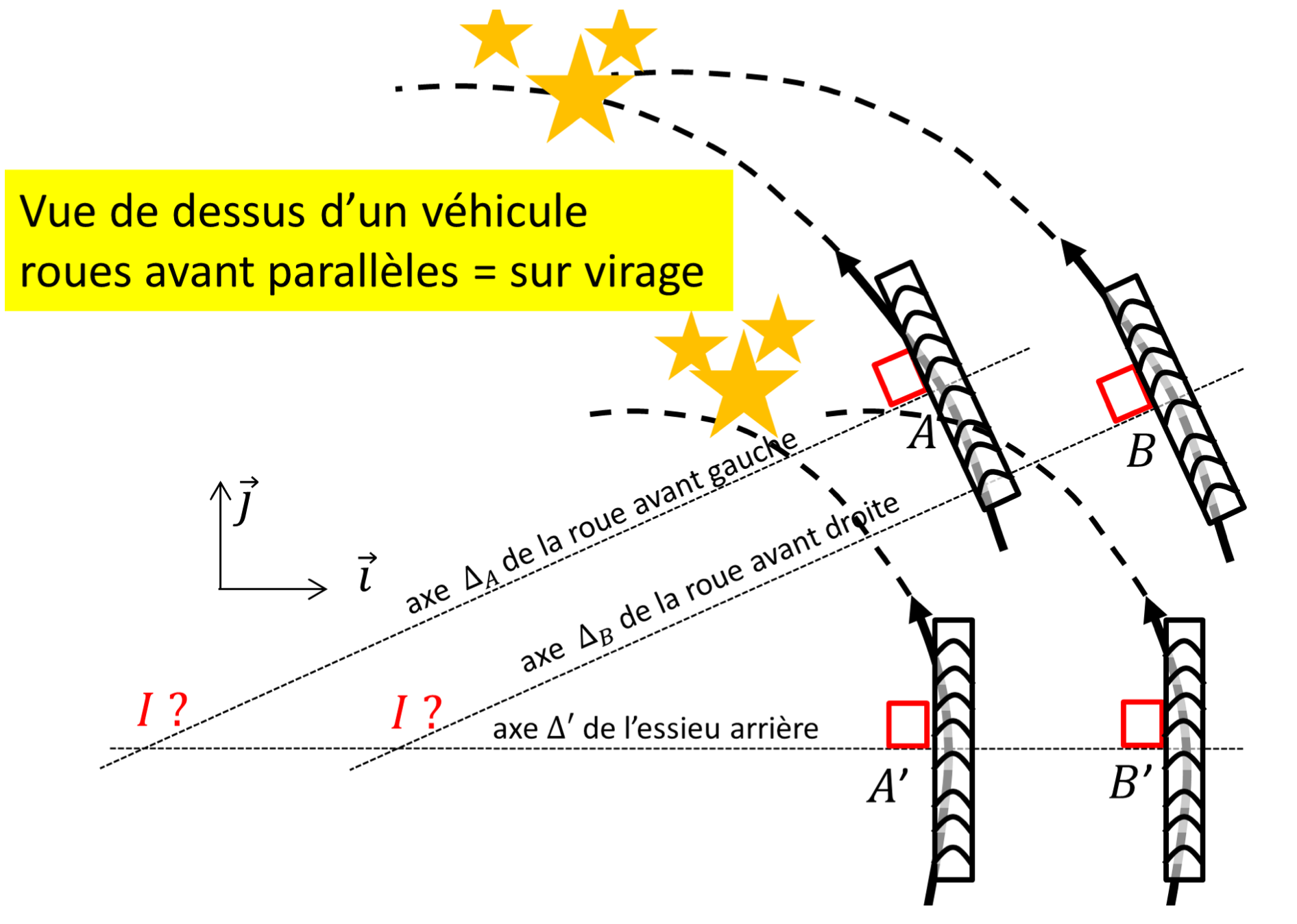
À tort, on croit souvent que les deux roues avant d'une voiture restent toujours parallèles. Il est vrai qu'un garagiste vérifie le «parallélisme» lors d'une révision — mais c'est celui des deux essieux, et qu'en modélisme les maquettes bon marché reproduisent le système de direction au moyen d'un «parallélogramme» déformable, figure 6 — mais cette approche est grossière. Elle laisse penser qu'il aura suffi, en quelque sorte, d'atteler et solidariser côte à côte deux bicyclettes. En courbe, les arcs de cercle qu'emprunteraient les roues avant ne seraient jamais concentriques, figure 7. Or le véhicule ne tourne en bloc que s'il y a un unique centre de rotation. Plus précisément la roue avant de droite est anormalement tournée vers la gauche. Ce braquage excessif tend à raccourcir la courbe en orientant le véhicule trop à l'intérieur du virage : il y a survirage. Les pneus ripent. À vitesse élevée, ils n'adhèrent plus ; c'est le tête-à-queue.

L’original à gauche. Une maquette au 1 : 24 à droite ; la direction comprend un rectangle articulé qui, en se pliant, se déforme en parallélogramme.
La première solution historique à ce problème, imaginée par le constructeur automobile Jeantaud13 (probablement inspiré par un brevet d'Ackermann14), fut d'articuler les roues avant, non pas à un rectangle, mais à un trapèze isocèle, figure 8. En se déformant, ce dernier accentue mécaniquement l'angle de la roue située à l'intérieur de la courbure. La roue extérieure peut ainsi suivre un cercle de même centre mais de plus grand rayon que celui de la roue intérieure. On peut positionner l'essieu arrière à la hauteur de ce centre quand on considère que le véhicule prend le virage le plus serré dans les conditions normales de conduite. Cela ne signifie pas que, sur des virages plus doux, les cercles soient encore concentriques. Ils ne le sont d'ailleurs plus. Mais on tolère dans ces situations moins dangereuses un léger patinage, reconnaissable aux crissements qu'il génère lorsqu'on se gare dans un parking souterrain par exemple.
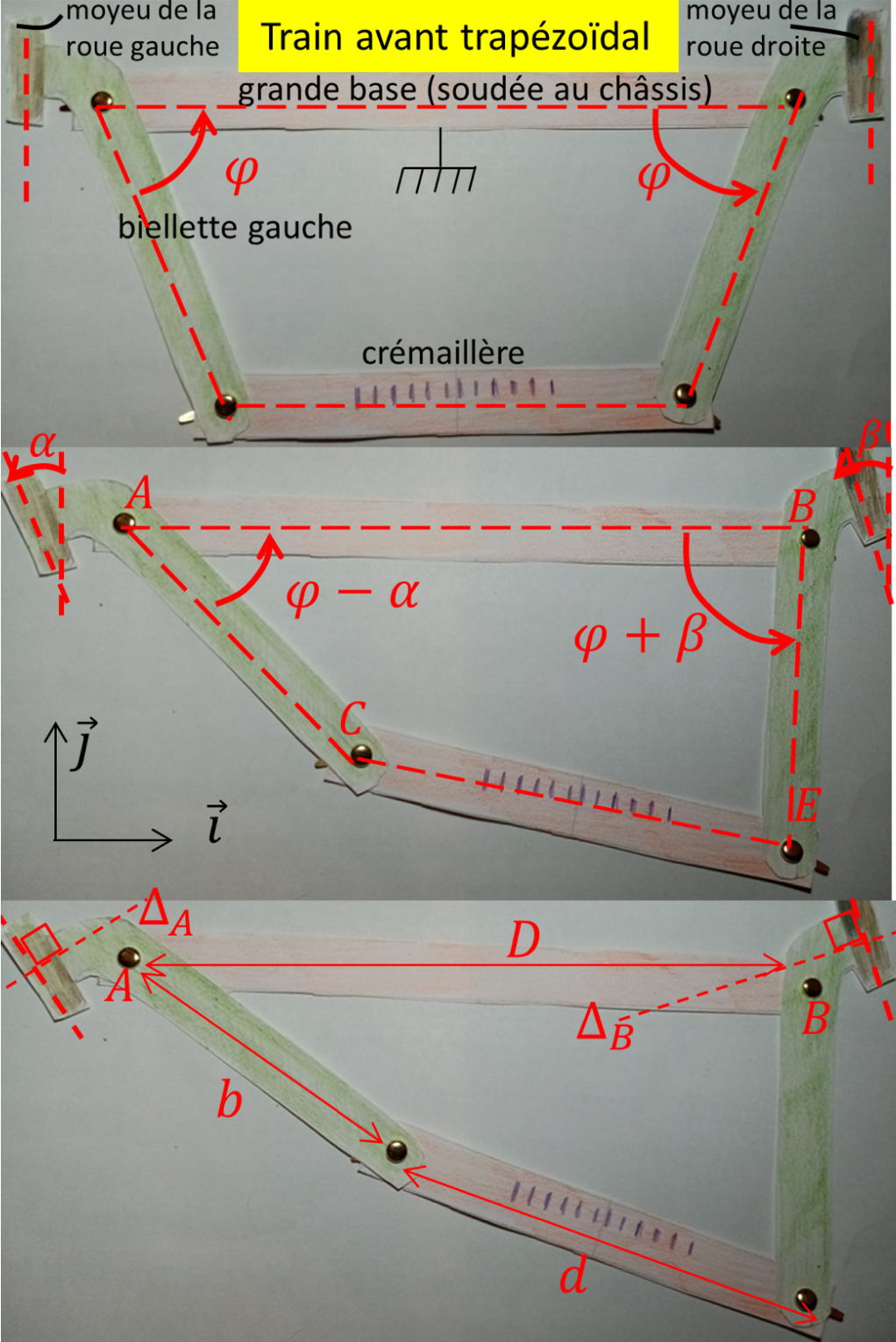
Train avant à géométrie trapézoïdale, successivement en ligne droite, en virage, en virage serré. La grande base fait corps avec le châssis. Se meuvent les deux biellettes de direction ainsi que la petite base, laquelle supporte une crémaillère qu’actionne un pignon (non représenté) issu de la colonne de direction (non représentée).
La chaîne cinématique
Pour mieux appréhender la chaîne cinématique qui est en jeu, rien ne vaut tant que de la fabriquer et de la simuler.
La fabrication ne demande qu'un petit matériel : du carton, une paire de ciseaux, des attaches parisiennes. La grande base du trapèze est fixée au châssis. La petite base est mobile, entraînant dans son mouvement les deux roues avant grâce au déplacement des petits côtés, appelés biellettes de direction, figure 8 ; au repos et en action. C'est la rotation du volant qui, par l'intermédiaire de la colonne de direction (non représentée), imprime le déplacement de la petite base via un pignon (non représenté) engrenant une crémaillère.
La simulation nécessite GeoGebra : une appliquette dédiée accompagnée d'une capsule vidéo expliquant sa prise en main sont disponibles en ligne ci-après.
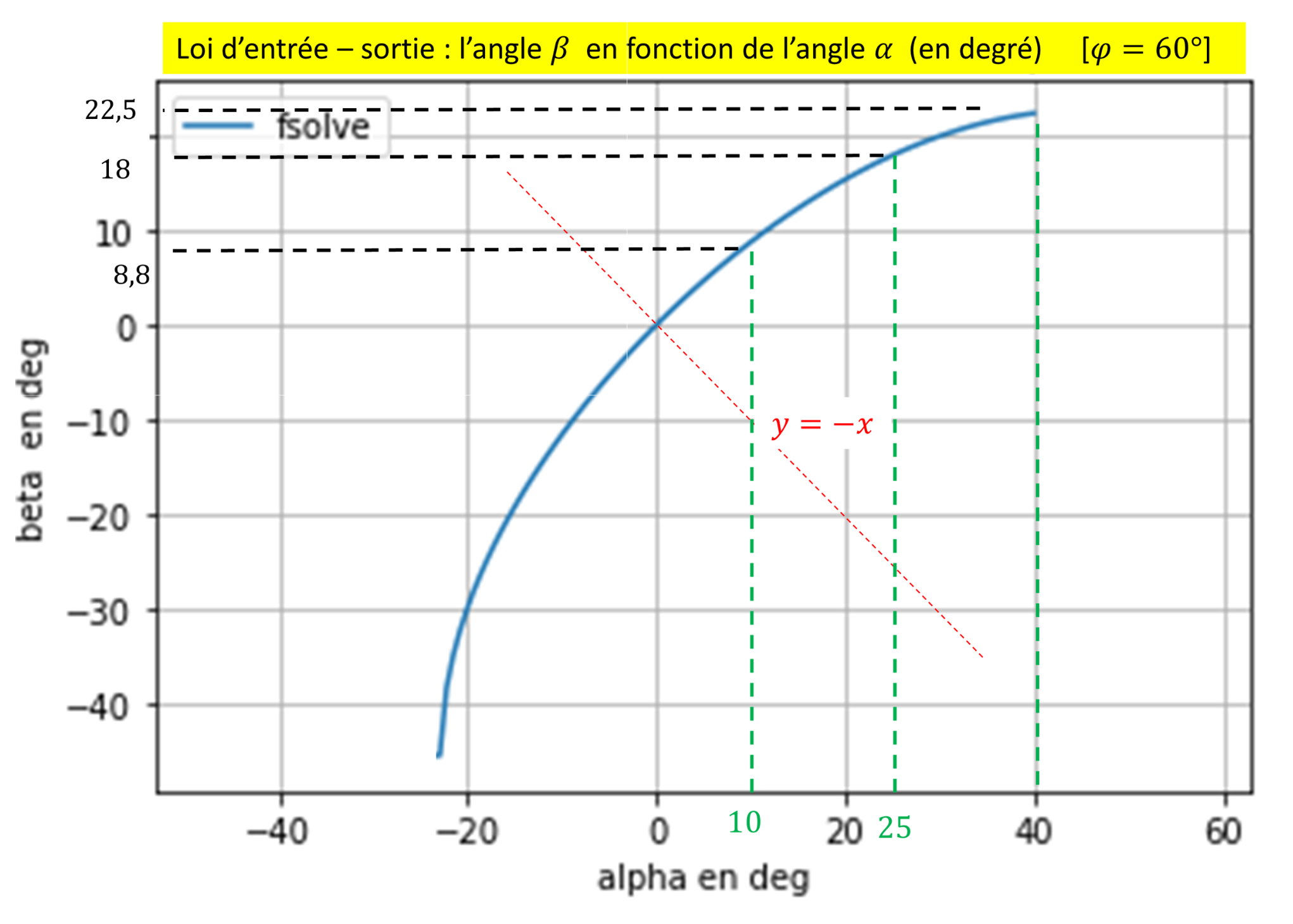
On construit d'abord le quadrilatère $ABCE$ qui, au repos, est un trapèze isocèle. Pour cela, on définit la grande base $AB$ de longueur $D$. On assujettit l'extrémité mobile $C$ de la biellette gauche au cercle de centre $A$ et de rayon $b$ (paramétrable à l'aide d'un curseur). De $C$ part la petite base, de seconde extrémité $E$ et de longueur $d$ égale à $ d = D - 2b\cos\varphi $ où $\varphi$ désigne l'angle intérieur aigu du trapèze. Le point $E$ est à la croisée du cercle de centre $C$ de rayon $d$ et du cercle de centre $B$ de rayon $b$. En déplaçant $C$ sur son cercle, on pivote plus ou moins la roue gauche de l'angle $\alpha$ (paramétrable), et la roue droite de l'angle $\beta$ (égal à $\alpha$ quand le trapèze est un rectangle, c'est-à-dire quand $\varphi = \frac{\pi}{2}$). Les axes des deux roues avant s'intersectent au point $I$, à la hauteur duquel il convient idéalement de placer l'essieu arrière. Bien sûr, celui-ci n'est réglé qu'une seule fois, dans une position définitive pour laquelle un (et un seul) virage est parfait, figure 9. En pratique il peut s'agir du tournant le plus sévère, à l'appréciation du constructeur. Sur notre schéma, la course de l'angle $\alpha$ va jusqu'à $40^\circ$, et l'on relève l'angle $\beta$ correspondant. Par exemple, pour $D=4$, $b=1$, $\varphi = 60^\circ$, on obtient $d = 3$, et quand on tourne la biellette gauche de $\alpha=10^\circ$, celle de droite tourne de $\beta\simeq 8,79^\circ$ (et logiquement, d'un peu moins). Un échantillon de valeurs de $\alpha$ fournit le tableau de valeurs (approchées), figure 10.
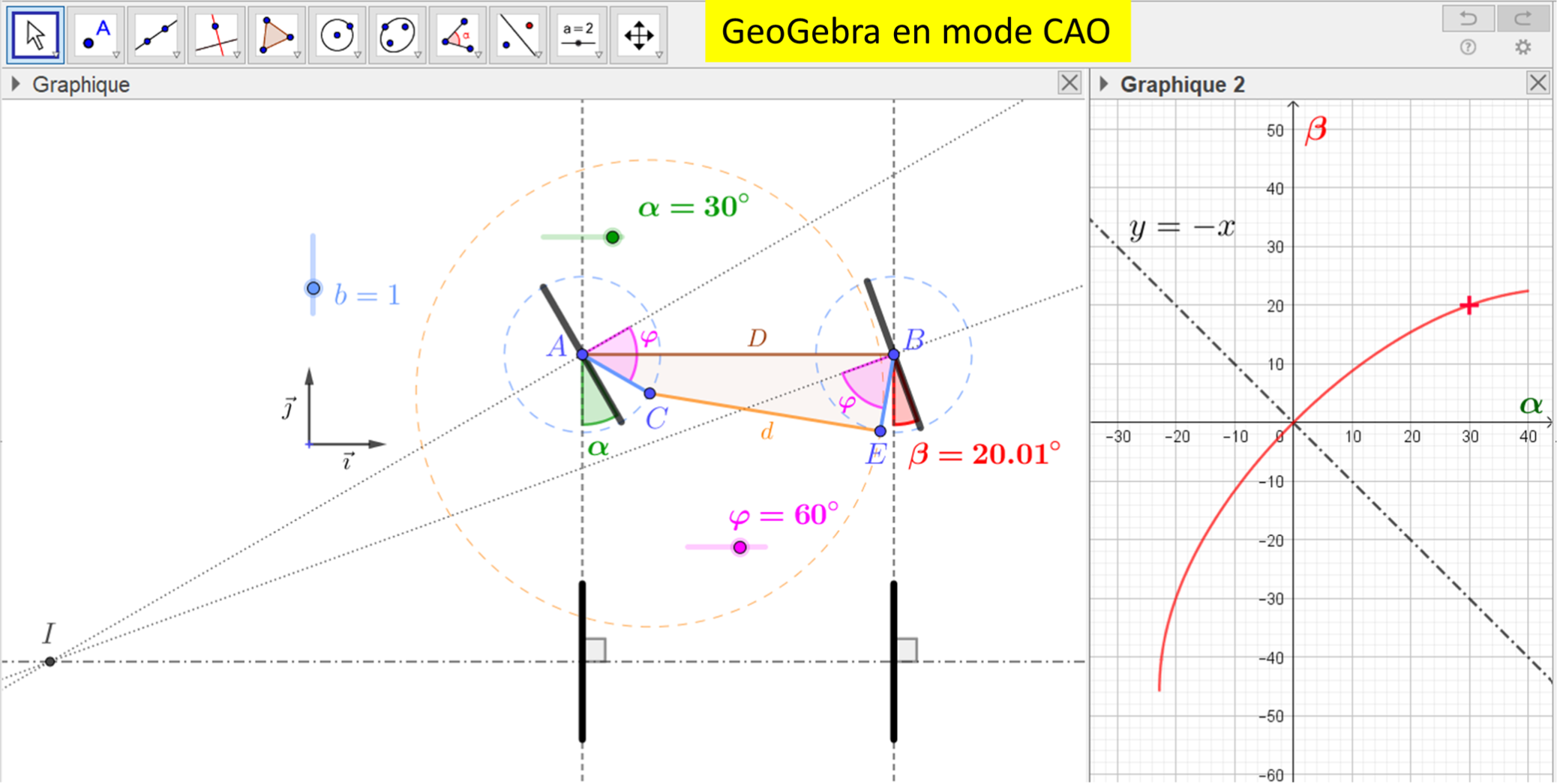
Ici, $\varphi = 60^\circ$. La courbe expérimentale de $\beta$ fonction de $\alpha$ dessinée à droite sera retrouvée par le calcul un peu plus loin, en figure 11.
$$ \begin{array}{|r|r|r|r|r|r|r|r|r|} \hline \alpha & 0^\circ & 10^\circ & 15^\circ & 20^\circ & 25^\circ & 30^\circ & 35^\circ & 40^\circ \\ \hline \beta & 0^\circ & 8,79^\circ & 12,36^\circ & 15,43^\circ & 17,98^\circ & 20,01^\circ & 21,52^\circ & 22,45^\circ\\ \hline \end{array} $$
Une manière alternative d'effectuer la simulation consiste à calculer analytiquement $\beta$ en fonction de $\alpha$. Partons de la fermeture vectorielle $$ \overrightarrow{CE}=\overrightarrow{CA} + \overrightarrow{AB} + \overrightarrow{BE}. $$ En projetant cette identité sur les directions $\overrightarrow{i}$ et $\overrightarrow{j}$ d'une une base orthonormée du plan, il vient : $$ x_{\overrightarrow{CE}} = -b\cos(\varphi-\alpha)+D-b\cos(\varphi+\beta) $$ et $$ y_{\overrightarrow{CE}} = b\sin(\varphi-\alpha)-b\sin(\varphi+\beta). $$ Donc, en passant au carré de la norme, $$ ||\overrightarrow{CE}||^2 - d^2= 0. $$ D'où l'équation reliant implicitement $\beta$ à $\alpha$ : $$ \left(b\cos(\varphi-\alpha)-D+b\cos(\varphi+\beta) \right)^2 + b^2 \left(\sin(\varphi-\alpha)-\sin(\varphi+\beta) \right)^2 -d^2= 0. $$ Il suffit alors d'en programmer la résolution approchée, par exemple sur Python en chargeant les bibliothèques ad hoc.
import numpy as np from scipy.optimize
import fsolve
import pylab as plt
from math import *
D = 4 #grande base
b = 1 #biellette
phi = 60*pi/180 #conversion en rad de 60 deg
d = D - 2*b*cos(phi) #petite base
#################################
#Membre gauche equation implicite
#################################
def Implicite(beta):
return (b*cos(phi-alpha)+b*cos(phi+beta)-D)**2\
+(b*sin(phi-alpha)-b*sin(phi+beta))**2-d**2
####################################
#Calcul de beta en fonction de alpha
####################################
#alpha varie de -30 deg à 40 deg,100 graduations
anglesAlpha = np.linspace(-30, 40, 100)
#résolution par scipy
anglesBeta=[0]*len(anglesAlpha)
for i in range(len(anglesAlpha)):
alpha=anglesAlpha[i]*pi/180 #conversion en rad
anglesBeta[i]=fsolve(Implicite,alpha)*180/pi
# fsolve recherche un zero de Implicite pres de alpha
################################################
#Tracé de la courbe de beta en fonction de alpha
################################################
plt.plot(anglesAlpha,anglesBeta,label='fsolve')
plt.legend()
plt.grid(True)
plt.xlabel('alpha en deg')
plt.ylabel('beta en deg')
plt.title('loi entree sortie : beta fonction de alpha')
plt.grid(True)
plt.axis('equal')
plt.show()
Le graphe obtenu en figure 11 confirme les valeurs du tableau de la figure 10. Sa symétrie vis à vis de la deuxième bissectrice était prévisible : elle procède de la symétrie de la voiture par rapport à son plan médiateur. En effet, si la roue gauche (resp. droite) est à l'intérieur (resp. extérieur) du virage après avoir tourné d'un angle $\alpha$ (resp. $\beta$), alors la roue droite (resp. gauche) est à l'intérieur (resp. extérieur) du virage après avoir tourné d'un angle $-\alpha$ (resp. $-\beta$). Au point $(\alpha,\beta)$ du graphe correspond le point $(-\beta,-\alpha)$, également sur le graphe.
Pour aller plus loin
La réflexion menée sur le vélo pourrait être développée. Voici quelques pistes :
- Nous l'avons entrevu au début de l'article : en virage et sur un mouvement circulaire uniforme (pour simplifier), le vélo est essentiellement soumis à sa force de pesanteur, verticale et ramenée en son centre de gravité, laquelle est compensée par la réaction du sol appliquée aux points de contacts entre les deux roues et le sol, et à la force de frottement (force qualifiée de centripète dans ce contexte) du sol également appliquée aux points de contact entre les roues et le sol, qui l'empêche d'être débordé par la force centrifuge. La force centrifuge augmente avec la vitesse de rotation et la masse 1516. Au-delà d'une valeur seuil, qui dépend du revêtement et de l'état des pneus, le sol n'est plus en capacité d'annuler la force centrifuge. D'après la loi de frottement de Coulomb17, le frottement sec statique devient dynamique, le vélo se met à glisser et quitte la piste.
- Nous pourrions évoquer le comportement d'un vélo roulant, cette fois, en ligne droite mais sur un devers. Le frottement du sol applique aux roues une force dans la direction et le sens ascendant de la plus grande pente. Sauf à résister avec le guidon, cela oriente naturellement la roue avant dans le sens descendant de la plus grande pente. La roue avant pivote et le vélo plonge.
- Nous pourrions aussi considérer le cas d'un vélo initialement à l'arrêt, dont la roue avant n'est pas bien alignée avec le cadre, mais que l'on pousse d'une main posée sur la selle afin de le faire avancer en ligne droite (pour le sortir de son garage par exemple). Le frottement du sol va de l'avant à l'arrière et rabat une fois de plus spontanément la roue avant.
Une vraie voiture, c'est évidemment plus compliqué qu'en jouet. Voici quelques subtilités que nous avions soigneusement éludées mais qu'il faut avoir en tête en guise d'approfondissements :
- Nous l'avons compris : en virage, les deux roues latérales situées à l'intérieur d'un virage parcourent moins de chemin que leurs homologues situées de l'autre côté. Les roues extérieures tournent donc plus vite. À l'arrière, ce n'est pas gênant : les deux roues sont en général indépendantes18. À l'avant, elles sont motrices. L'arbre moteur, qui les entraîne, doit par conséquent doser la puissance qu'il transmet à l'une ou à l'autre : c'est tout le rôle du différentiel.
- L'essieu arrière est droit. La géométrie à l'avant est nécessairement plus complexe car en virage les roues ne sont plus perpendiculaires aux demi-arbres de transmissions issus du différentiel. On interpose donc des joints de Cardan19 (du mathématicien éponyme), comme sur les manivelles d'un volet roulant.
- Même en ligne droite, les roues ne sont ni exactement parallèles , ni parfaitement perpendiculaires au sol, parfois de façon tout à fait volontaire. Elles peuvent être légèrement pincées, comme on disposerait ses skis lorsqu'on freine en chasse-neige. Il arrive aussi qu'elles soient carrossées ou contre carrossées, c'est-à-dire qu'on leur fasse prendre un carre en forme de Genu Varum ou de Genu Valgum, comme sur les engins de chantier ou les voitures de rallye.
- Comme sur un vélo, un angle de chasse permet aux roues avant de se réaligner naturellement au sortir d'un virage.
- L'articulation trapézoïdale de Jeantaud n'est satisfaisante que dans une configuration géométrique donnée. Aujourd'hui, la direction du train avant est plus élaborée, comme on peut l'observer sur la maquette très réaliste photographiée en figure 12.
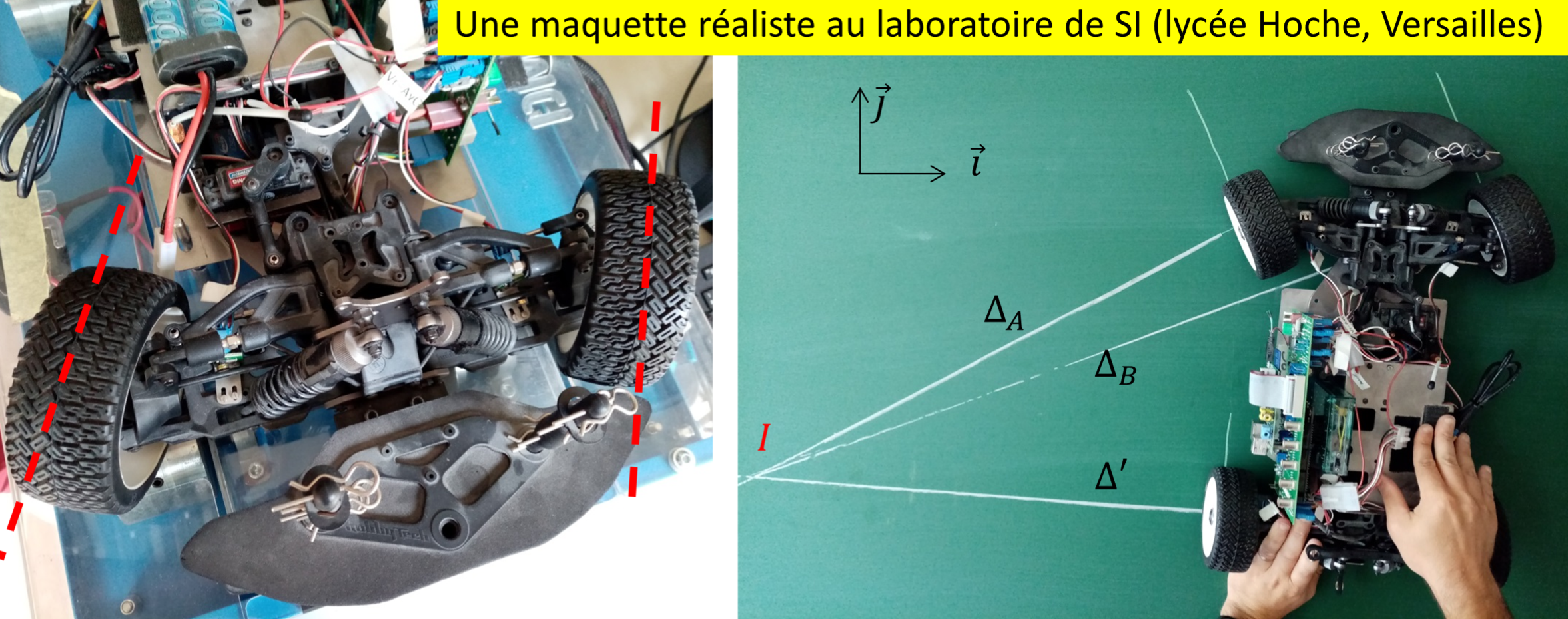
Sur cette maquette très réaliste, l'articulation du train avant (photo de gauche) ne se résume pas à un trapèze déformable. Plus technique, elle permet en toutes circonstances un comportement quasi parfait en virage (photo de droite). Laboratoire de SI, lycée Hoche (Versailles).







