Quelle est la probabilité que ma part contienne la fève ? Posée ainsi, la réponse est simple. Ayant par exemple coupé en huit le fameux gâteau, j'ai une chance sur huit d'avoir la fève.

Maintenant, imaginons que les parts soient données et consommées au fur et à mesure. Le premier convive est servi, mange sa part et ne trouve pas de fève. Il est clair qu'au fur et à mesure que mes prédécesseurs consomment et ne trouvent pas la fève, ma probabilité d'avoir la fève augmente. Si je suis le troisième dans la liste, les deux premiers n'ayant rien obtenu, ma probabilité d'avoir la fève a augmenté pour être maintenant de 1/6.

Mais... est-ce si sûr ?

Il se pourrait bien qu'un doute surgisse ! Le pâtissier n'aurait-il pas oublié de mettre une fève dans cette galette ? Cela est toujours possible, d'autant plus que mon pâtissier est connu pour sa distraction. En effet, il parait qu'il oublie de mettre une fève une fois sur cinq.

Vous percevez alors le problème : plus il y aura eu de parts consommées avant vous (sans fève), plus la probabilité qu'il y ait une fève diminue mais moins il reste de parts ! Alors, au fur et à mesure que les autres parts sont consommées (sans fève), quelle est la probabilité que votre part contienne la fameuse fève ?

Pour calculer la probabilité que votre part contienne une fève, il faut dans un premier temps calculer la probabilité que la galette contienne une fève en fonction du nombre de parts mangées et du fait qu'aucune fève n'ait encore été trouvée. Ensuite, il suffit de diviser chaque probabilité par le nombre de morceaux de galette restants.

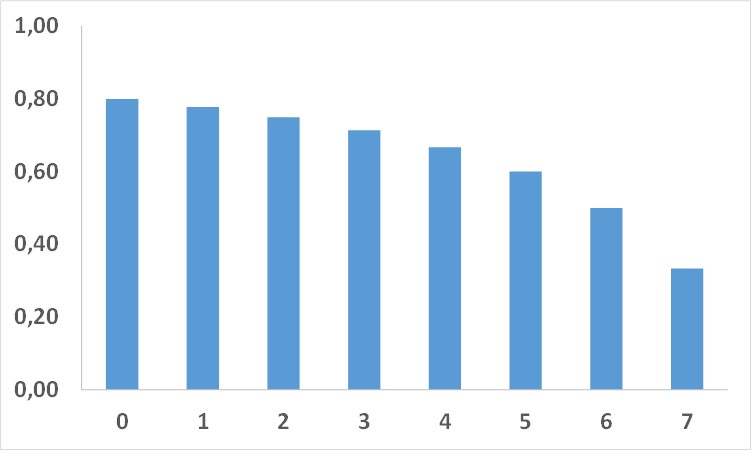
D'abord le graphique de la probabilité qu'il y ait une fève en fonction du nombre de parts déjà mangées :

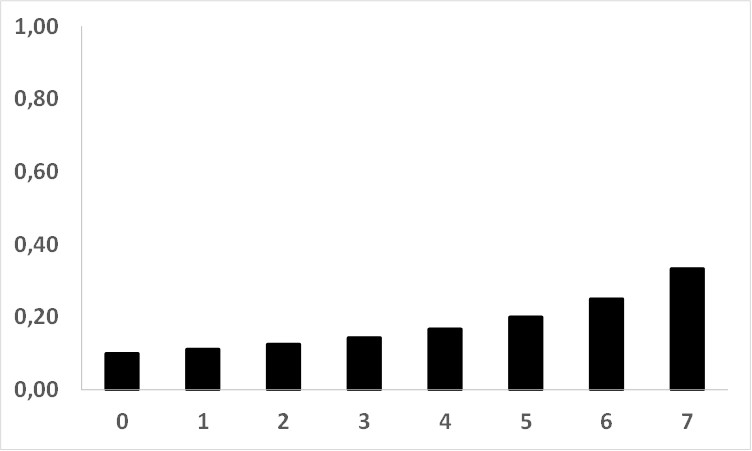
Puis la probabilité que votre part ait la fève :

Et voilà ! Au fur et à mesure que vos prédécesseurs n'ont pas trouvé de fève, la probabilité qu'il y ait une fève diminue mais la probabilité que vous ayez la fève augmente quand même. Si vous êtes le dernier à consommer, la probabilité d'avoir la fève est ici de 1/3.

Le principe du calcul : Tant que personne n'a mangé sa part, la probabilité qu'il y ait une fève est de 0,8 et il y a 8 parts. La probabilité que j'ai la fève est donc de $0,8/8=1/10$. Maintenant l'un des autres convives mange sa part et ne trouve pas de fève. Il faut calculer la probabilité $P(1_{F})$ qu'il y ait une fève dans cette galette sachant qu'il s'est avéré qu'un convive n'a pas trouvé de fève (événement $E_{0/1})$.

$$ P(1_{F}|E_{0/1})=P(E_{0/1}|1_{F})\times\dfrac{P(1_{F})}{P(E_{0/1})} $$

Il est clair que $P(E_{0/1}|1_{F})=7/8$ et on sait que $P(1_{F})=0,8$.

$$ P(E_{0/1})=P(E_{0/1}|1_{F})\times P(1_{F})+P(E_{0/1}|0_{F})\times P(0_{F})=\dfrac{9}{10} $$

Aussi, on obtient que $P(1_{F}|E_{0/1})=7/9$ et la probabilité que votre part contienne une fève est maintenant de $1/9$. Et ainsi de suite...

Bon appétit !