Zéro + Zéro = la boule à Zéro (et la tête à Toto)
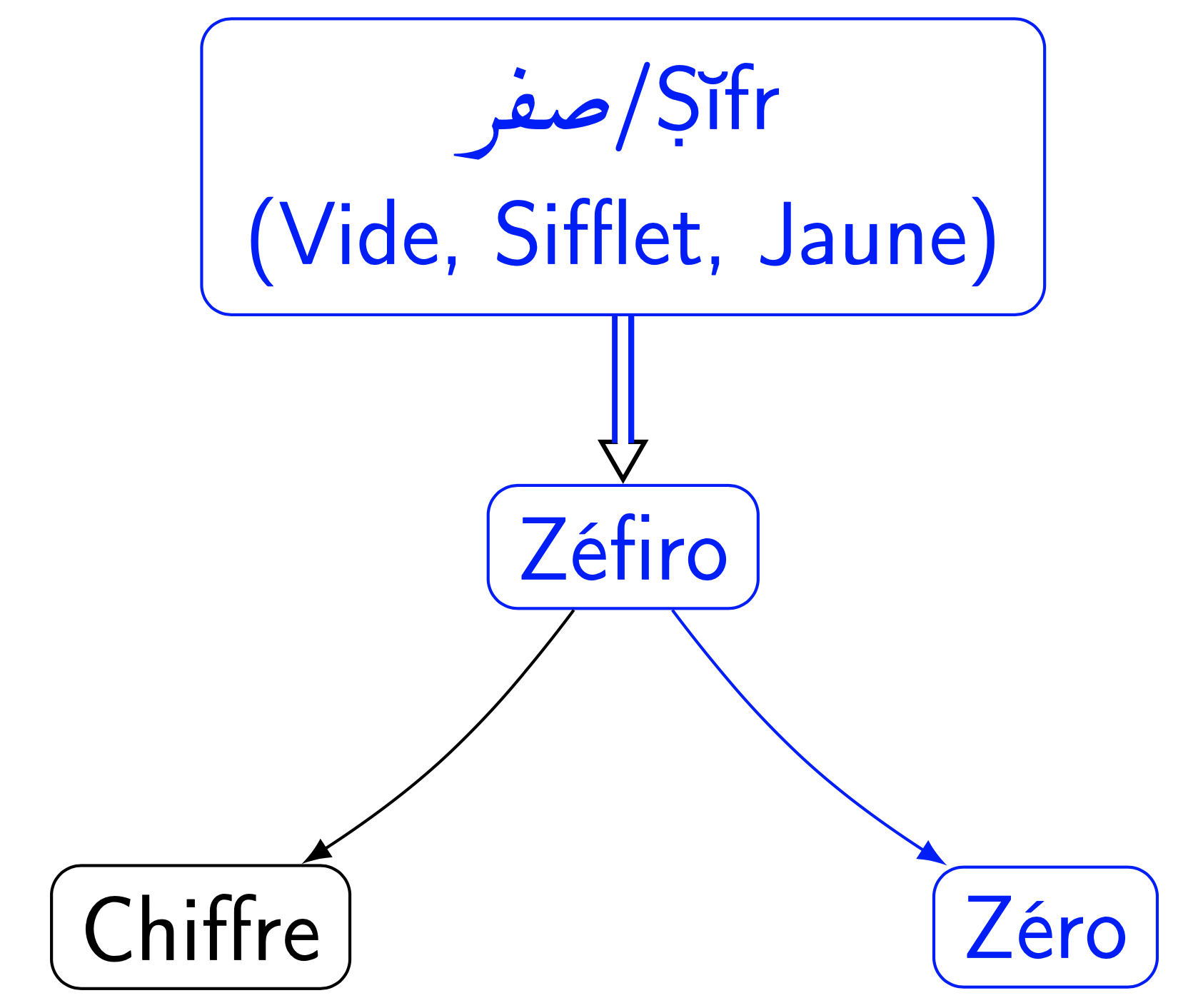
Comment pouvait-il en aller autrement du Zéro? Originaire d'Inde, mais emprunté à l'arabe « صفر » (prononcer Ṣĭfr) qui signifie le « Vide » ou la « Vacance », un « Sifflement de l'air » (souvent léger) ainsi qu'une « Couleur jaune » (plutôt pâle) et bien sûr le « Nombre nul », il devint par consonnance1 « Zéfiro » une fois passé dans l'Occident du Moyen Âge, formant ensuite les mots « Chiffre » et « Zéro », de ce fait de même souche 2345.
C'est Fibonacci1 qui aurait introduit le mot « Zéfiro », pour sa ressemblance avec l'arabe. Le Dieu grec « Zéphyr » (incarnation mythologique d'un vent doux de l'ouest) dont — heureux hasard — à la fois la sonorité et le sens se rapprochent, l'aurait-il également inspiré ? Peut-être. L'expression « c'est du vent ! », aujourd'hui si courante, et les notations « 0 » et « $\emptyset$ », si voisines, offrent ainsi différents reflets.
Comme pour la somme, il en va du produit $$\text{« } {\color{blue}{\mathrm{Zéro}}} \ \times \ {\color{blue}{\mathrm{Zéro}}} \text{ »}, $$ lui aussi réduit au néant.
Étrangement, la puissance \[\text{« } {\color{blue}{\mathrm{Zéro}}}^{ {\color{blue}{\mathrm{Zéro}}}} \text{ »} \] fait bande à part. Mieux, à valoir « Un » elle recrée l'unité tout en partant de rien. C'est qu'il le faut bien pour lire correctement en classe de Terminale 1, dans la formule du binôme \[(a+b)^n = \sum_{k=0}^n \binom{n}{k}a^kb^{n-k},\] le premier terme $ \binom{n}{0}a^0 b^{n}$ ou le dernier $\binom{n}{n}a^n b^{0}$ si, cas particulier un peu bête mais fréquent, l'un des deux opérandes $a\in\mathbb{R}$ ou $b\in\mathbb{R}$ est nul.
C'est qu'il le faut encore pour évaluer convenablement le polynôme \[ P(X) = \sum_{k=0}^n a_k X^k \] en $0$ et recueillir $a_0 0^0 = a_0$, son coefficient constant 1. Nécessité fait loi, pour ainsi dire.
Mais toute pratique qu'elles soit, la convention $0^0=1$ (équivalente par passage au logarithme à $0\times\infty = 0$, règle utilisée en théorie de la mesure 23), se fait trompeuse face aux limites, si dangereusement indéterminées, \[\text{« } \rightarrow {\color{blue}{\mathrm{Zéro}}} ^{ \rightarrow {\color{blue}{\mathrm{Zéro}}} } \text{ »}. \] On en croise certaines dès la classe de Première 4. Ainsi, par exemple,
- $(2^{-n})^{\frac{1}{n}}$ tend vers $\frac{1}{2}$ et non $1$ ;
- $(3^{-n})^{\frac{1}{n}}$ tend vers $\frac{1}{3}$ et non $1$ ;
- $(2^{-n})^{\frac{1}{\sqrt{n}}}$ tend vers $0$ et non $1$ ;
Quant à
- $(2^{-n})^{\frac{2+(-1)^n}{n}}$, il ne tend vers rien...
On pourra faire le lien avec cet autre écueil... redoutable, \[ \text{« } \rightarrow 1 ^{\rightarrow \infty} \text{ »}, \] puisque formellement \[ \text{« }\rightarrow 1 ^{\rightarrow \infty} = e^{\rightarrow \infty \ln(\rightarrow 1)} = e^{(\rightarrow -\infty)( \pm\ln(\rightarrow 1))} = \left(e^{\rightarrow -\infty}\right)^{ \pm\ln(\rightarrow 1)} = {\color{blue}{\mathrm{Zéro}}}^{ \rightarrow {\color{blue}{\mathrm{Zéro}}}} \text{ »}. \] Comme exemple iconique : $(1+\tfrac{x}{n})^n$, issu de la résolution numérique de l'équation différentielle $\big(y'=y ; y(0)=1\big)$ par la méthode de Newton, admet une limite. Et voilà qui peut conforter la définition de l'exponentielle au lycée 5.