Text

Round Robin Tournament is a well-known type of tournament format that sport schedulers use.

Let $N$ be an even number of teams in the tournament. At the end of a Round Robin Tournament every team should have played against every other team. This method assumes that there are enough fields / pitches / courts so that all the games in a round can be played simultaneously. The technique is called the polygon method. There will be $N-1$ rounds (each team will play $N-1$ games). Since each team will play every other team once, no team will be idle* during any of the rounds. Let us schedule a round-robin tournament for 8 teams numbered from $1$ to $8$.

• Draw a regular $(N-1)$ sided polygon (i.e. a heptagon for 8 teams). Each vertex and the centre point represents one team.

  

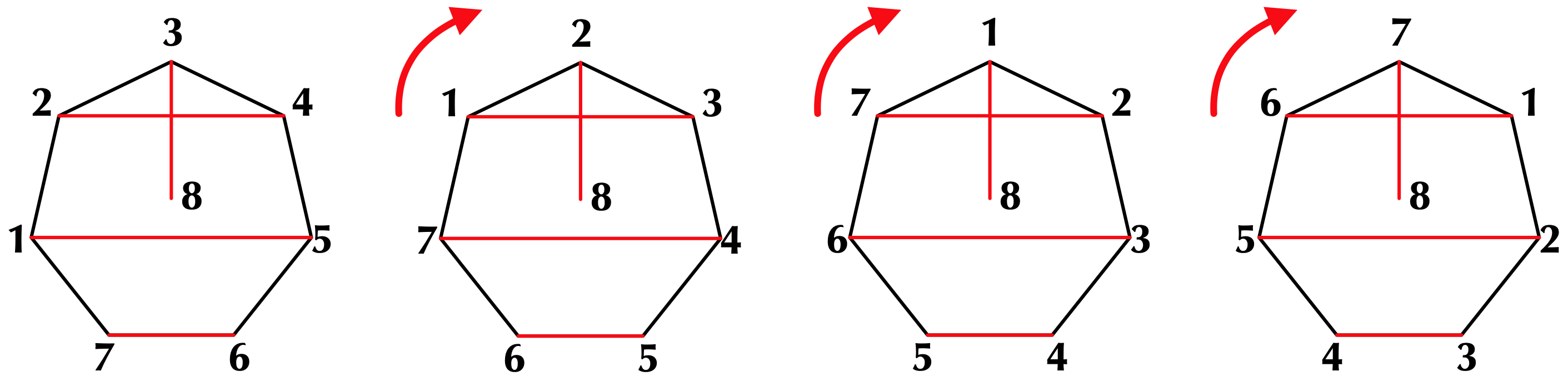
• Draw horizontal stripes as shown. Then, join the vertex that has been left out to the centre. Each segment represents teams playing each other in the first round. So $(7, 6)$, $(1, 5)$, $(2, 4)$ and $(3, 8)$ play in the first round.
• Rotate the polygon $1/(N-1)$th of a circle (i.e. one vertex point). The new segments represent the pairings for round two.
• Continue rotating the polygon until it returns to its original position.

Extract from an article by Arunachalam Y. published on nrich.maths.org

Questions

1. You are the organizer of a tournament with 6 teams, describe how many rounds you have and which team is playing versus which one in each round with the Round Robin method?
2. If you had to organize a tournament with 5 teams, how would you organize it?

Glossary

• scheduler: organisateur d’un planning
• idle: without work or activity

Audio

Version 1 (Laura Killian)

Version 2 (Jacob Chmielewski)

Additional Vocabulary

• pitch: terrain de sport
• vertex: sommet (plural: vertices)