La modélisation mathématique des épidémies peut se présenter sous la forme de systèmes d'équations différentielles ou d'équations aux dérivées partielles. Ceux-ci permettent notamment de rendre compte d'un certain nombre de phénomènes caractéristiques de leur propagation tels que les ondes progressives ou la re-contamination. Nous allons ici nous appuyer sur l'exemple de la diffusion de la rage dans une population de renards pour présenter quelques modèles de difficulté croissante.
Nous adopterons d'abord un point de vue global en modélisant le comportement de l'ensemble d'une population au cours du temps. Suivant la complexité du modèle considéré, c'est-à-dire suivant le nombre de phénomènes élémentaires pris en compte, on est conduit à l'étude de systèmes d'équations différentielles de difficulté variable.
Dans un second temps, nous introduirons une composante spatiale au problème : il s'agira d'étudier le comportement de l'épidémie au cours du temps et en chaque endroit d'un territoire. Étant donné que les inconnues du problème dépendent maintenant de deux variables, à savoir le temps et l'espace, les équations différentielles sont remplacées par des équations aux dérivées partielles.
Étude globale d'une population
Le modèle SIR
Dans le premier modèle que l'on souhaite présenter, les individus (les renards) peuvent se trouver dans 3 états différents : il y a des renards sains ($S$), des renards infectés ($I$), et des renards morts ($R$). Ce modèle très simple et bien connu est par exemple présenté en détails dans 1.
\begin{equation} \tag{SIR} \left\{ \begin{array}{l} S'= -r IS, \\ I'=rIS -\alpha I, \\ R' = \alpha I. \end{array} \right. \end{equation}
Au lieu de considérer les individus morts, on peut aussi utiliser ce modèle pour étudier une maladie pour laquelle les individus guérissent, et sont ensuite immunisés : il faut alors les distinguer des individus sains n'ayant jamais contractés la maladie.
Dans ce modèle, la première équation correspond au phénomène de contamination : lorsque cohabitent des individus sains et des individus infectés, un certain nombre d'individus sains sont infectés. Il est par ailleurs naturel de considérer ce terme comme proportionnel au produit $IS$ car la quantité de microbes dans l'air, donc la probabilité pour un individu sain donné d'être infecté, est proportionnelle à $I$. Il nous faut ensuite multiplier cette probabilité par le nombre d'individus sains, c'est-à-dire par $S$.
Pour ce qui est des variations de la fonction $I$, le premier terme correspond aux individus nouvellement contaminés. Le deuxième terme, en $- \alpha I$, correspond aux individus qui meurent.
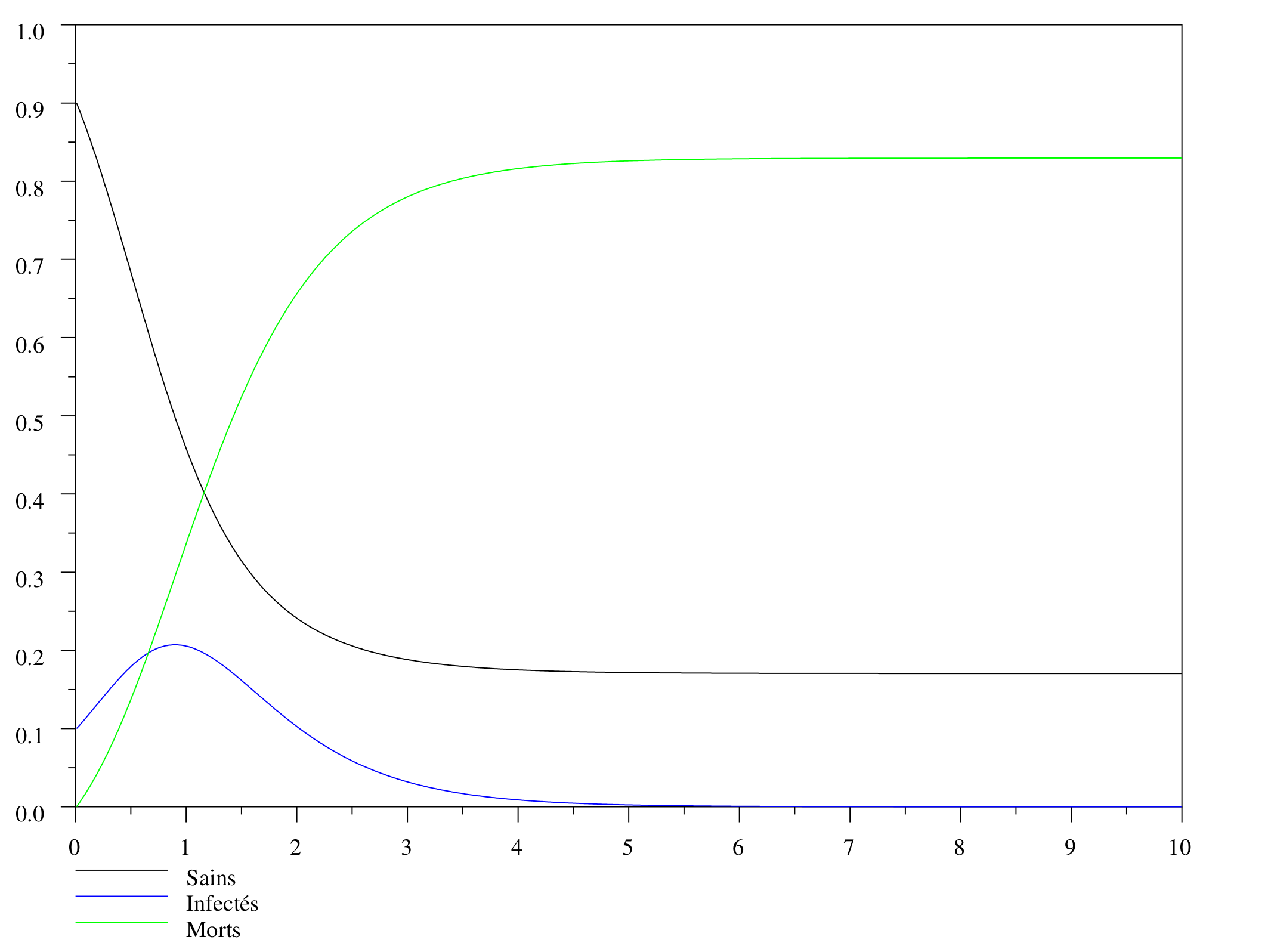
Un petit programme SIR que l'on peut utiliser en version matlab ou scilab permet de tracer l'évolution des populations $S$, $I$ et $R$ en fonction du temps. Selon les valeurs des paramètres $\alpha$ et $r$, les comportements sont complètement différents : si $\alpha$ est trop élevé par exemple, les individus infectés meurent presque tout de suite et n'ont pas le temps d'en infecter beaucoup d'autres. Voici un exemple d'évolution des populations au cours du temps, obtenu avec SIR pour les valeurs $r=4$ et $\alpha=2$.
Simulation pour le modèle SIR avec les valeurs $r=4$ et $\alpha=2$.
D'autres modèles pour d'autres épidémies
Il existe de nombreux modèles suivant les hypothèses que l'on fait sur la maladie étudiée. Il est souvent intéressant de définir plus de catégories de populations : ainsi, pour des modèles de maladies sexuellement transmissibles, on différenciera les populations suivant leur sexe, ce qui multiplie le nombre de possibilités par 2. Pour obtenir le système d'équations différentielles correspondant, il est utile de faire un schéma.
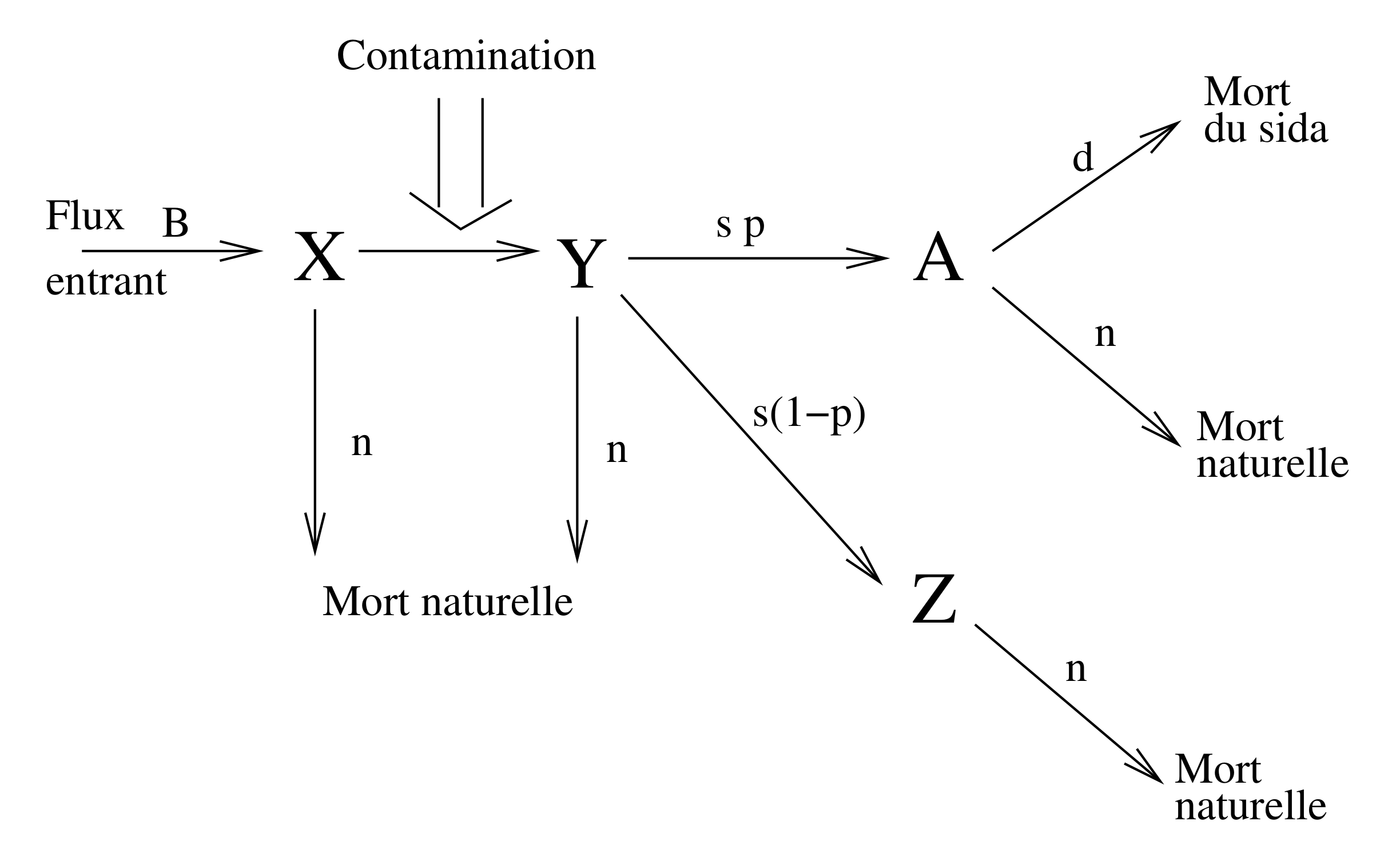
Ainsi, pour étudier une maladie de type sida, on peut par exemple considérer un modèle qui suit l'évolution de quatre groupes de population : les individus sains ($X$), les individus infectés ($Y$), les porteurs sains ($Z$), c'est-à-dire des individus ayant été infectés et désormais immunisés, et enfin les individus malades ($A$). Dans le schéma qui suit, les flèches entre les différents états représentent les transitions possibles entre les 4 groupes $X,Y,Z$ et $A$ pour un individu donné, avec les probabilités correspondantes.
En effet, du point de vue de l'étude du sida (et uniquement du sida), un individu donné, quel que soit son état, peut mourir d'autre chose que du sida, c'est ce que l'on range dans la catégorie « mort naturelle ». On considère qu'il y a un taux de mortalité fixe, noté $n$, et ce pour toutes les populations considérées (sains, infectés, malades ou porteurs sains).
D'autre part, un individu sain ($X$) peut aussi être contaminé, auquel cas il devient un individu infecté ($Y$). Un individu infecté peut lui évoluer vers deux stades possibles : malade ($A$) ou porteur sain ($Z$). Le nombre $s$ représente la vitesse d'évolution de la maladie : plus ce taux est grand, plus les individus infectés évoluent vite vers l'un des stades suivants ($A$ ou $Z$).
Le nombre $p$, compris entre $0$ et $1$, représente la probabilité pour que cette évolution se fasse vers l'état $A$ (malade). Bien sûr, si $p$ diminue, la quantité de porteurs sains, immunisés contre la maladie, augmente. La maladie est alors moins dangereuse globalement.
Enfin, un malade peut mourir de sa maladie, et ce avec un taux de mortalité $d$ considéré comme fixe, alors qu'un porteur sain et immunisé, ne peut plus évoluer du point de vue de cette maladie.
Toutes ces hypothèses conduisent à considérer un système d'équations différentielles de la forme :
$$\left\{ \begin{array}{l} X' = B - n X - \lambda_c X \\ Y' = \lambda_c X - (n+s) Y \\ A' = sp Y - (d+n)A \\ Z' = s(1-p) Y - n Z \end{array} \right. \quad \text{ où } \quad \lambda_c = \frac{\beta Y}{X+Y+Z+A}.$$
Le coefficient $\lambda_c$ représente un taux de contamination, qu'il est naturel de relier au rapport $Y/(X+Y+Z+A)$, probabilité lors d'une rencontre pour que la personne rencontrée soit infectée, donc contaminante.
Bien sûr, ce n'est qu'un modèle parmi beaucoup d'autres. Par ailleurs, le système différentiel obtenu devient rapidement assez compliqué dès que plusieurs interactions entre groupes de population sont prises en compte.
Modèles de diffusion
On s'intéresse à nouveau à la propagation de la rage dans une population de renards. Nous allons maintenant prendre en compte le fait qu'il peut y avoir des variations du nombre de renards non seulement au cours du temps mais aussi en fonction de leur position sur un territoire donné. Ce modèle et beaucoup d'autres est décrit en détails dans 1.
Équations du système
On s'intéresse ici à la répartition spatiale des populations saines et infectées, au lieu de les considérer uniquement dans leur totalité. On fait l'hypothèse que les individus sains ne bougent pas (ils respectent les territoires de leur voisins), en revanche les malades errent au hasard, ayant perdu la notion de territoire.
Si l'on note $S (t, x)$ et $I (t, x)$ les densité de renards sains et de renards infectés à la position $x$ et à l'instant $t$, ces quantités vérifient le système d'équations différentielles suivant.
\begin{equation}\tag{diffusion} \left\{ \begin{array}{l} \displaystyle\frac{\partial S}{\partial t} = -r IS \\ \displaystyle\frac{\partial I}{\partial t} = r IS - \alpha I + D \Delta I. \end{array} \right. \end{equation}
Dans le modèle SIR, les fonctions inconnues $S$ et $I$ ne dépendaient que du temps et les équations différentielles faisaient intervenir leurs dérivées $S'$ et $I'$. Dans ce modèle de diffusion, les fonctions $S$ et $I$ dépendent de deux variables, $t$ et $x$, et les dérivées de ces fonctions par rapport à la variable $t$ sont notées $\frac{\partial S}{\partial t}$ et $\frac{\partial I}{\partial t}$. Ce sont des dérivées partielles.
Le terme $D \Delta I$ qui apparaît dans l'expression de la dérivée temporelle de $I$ correspond à la dispersion spatiale des individus malades. Nous allons le définir précisément dans le paragraphe suivant.
Notion de diffusion
Le phénomène de dispersion des renards malades est modélisé par un terme de diffusion. On peut le décrire comme la résultante macroscopique de déplacements « anarchiques » et « chaotiques » des renards infectés. La constante $D$ mesure l'intensité de cette diffusion.
Supposons un instant que l'on modélise la propagation de la maladie avec des variables discrètes en espace et en temps : on mesure le nombre de renards infectés à un certain nombre d'emplacements régulièrement espacés (par exemple tous les kilomètres). De plus, on effectue ces mesures à intervalle de temps régulier, par exemple tous les jours. Ce phénomène de diffusion correspond alors au phénomène suivant : chaque jour, une proportion donnée de la population des renards malades d'un emplacement donné se déplace vers les deux emplacements voisins, à 1 km à droite et à gauche de l'emplacement de la veille.
Cette discrétisation du problème, c'est-à-dire le fait de remplacer les variables continues $t$ et $x$ par des variables discrètes, permet non seulement de comprendre le sens du modèle mais permet également de faire des simulations numériques comme celles qui seront présentées plus bas.
Le terme $\Delta I$ est appelé laplacien de la fonction $I$. C'est l'analogue continu de ce phénomène de diffusion que l'on vient de décrire pour des variables discrètes. Comme on ne considère ici qu'une dimension spatiale, le laplacien de $I$ n'est autre que la dérivée seconde par rapport à la variable d'espace $x$ : $\Delta I = \frac{\partial^2 I}{\partial x^2}$. Ainsi dans ce cas particulier, $\Delta I$ est la dérivée partielle d'ordre $2$ de $I$ par rapport à la variable $x$.
Propagation d'onde
On rappelle que l'on suppose que la dimension d'espace est $1$, c'est-à-dire que les renards vivent et se déplacent sur une ligne droite.
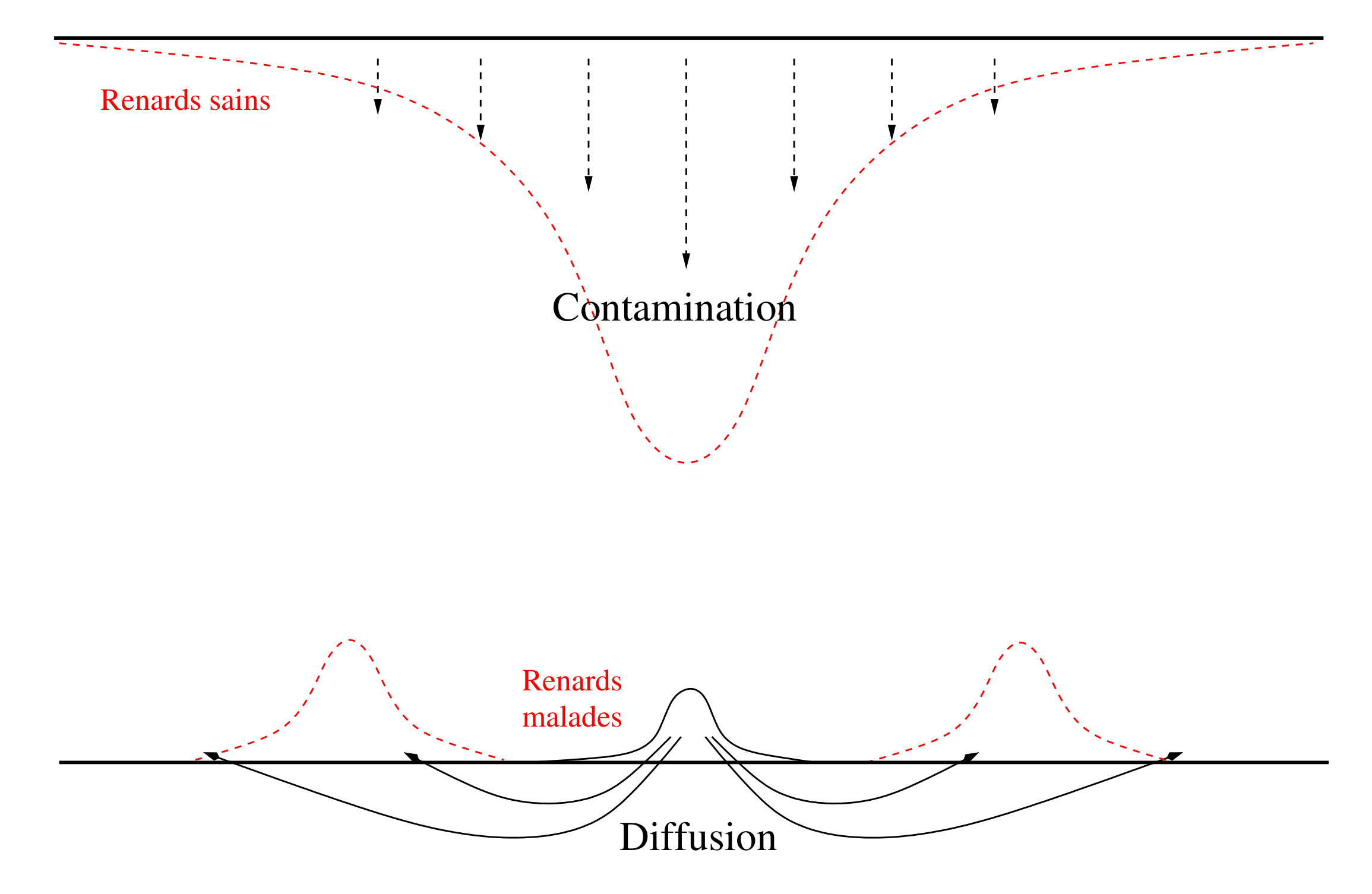
Si l'on introduit une petite quantité de renards infectés à un endroit, ces individus vont de par leur comportement anarchique « diffuser » : une partie d'entre eux va se déplacer vers d'autres zones, respectivement à gauche et à droite de l'endroit où ils ont été introduits. Là, ils contamineront la population saine, augmentant d'autant leur nombre. Tout ceci va créer deux vagues d'épidémie : l'une vers la gauche et l'autre vers la droite. Enfin, certains individus infectés meurent et c'est ainsi que parallèlement à la création de populations infectées des deux côtés de l'endroit où la maladie a été introduite, la bosse initiale disparaît peu à peu.
Sur cette figure, sont représentées d'une part la répartition de la population des renards sains, en haut, et d'autre part la répartition des renards infectés, en bas. Initialement, il y a une répartition uniforme de renards sains (ligne droite supérieure) et quelques renards localisés autour d'un point (la petite bosse en trait plein au dessus de la ligne droite inférieure).
On voit ensuite la population de renards sains diminuer au centre et la population de renards infectés se séparer en deux ondes qui partent respectivement à gauche et à droite.
Ensuite, ces deux vagues se propagent tout naturellement : de proche en proche, certains individus infectés vont aller vers la zone saine et y contaminer d'autres individus. Tout ceci va faire augmenter assez fortement la quantité d'individus infectés à proximité immédiate de la zone infectée, diminuant par là même la quantité d'individus sains, d'où un déplacement global de la population infectée. Il y a certes aussi diffusion d'individus infectés autour du foyer initial, mais comme il y a beaucoup moins d'individus sains qu'au départ, la contamination qui en résulte est négligeable : ces individus meurent peu à peu, c'est tout.
Des simulations numériques
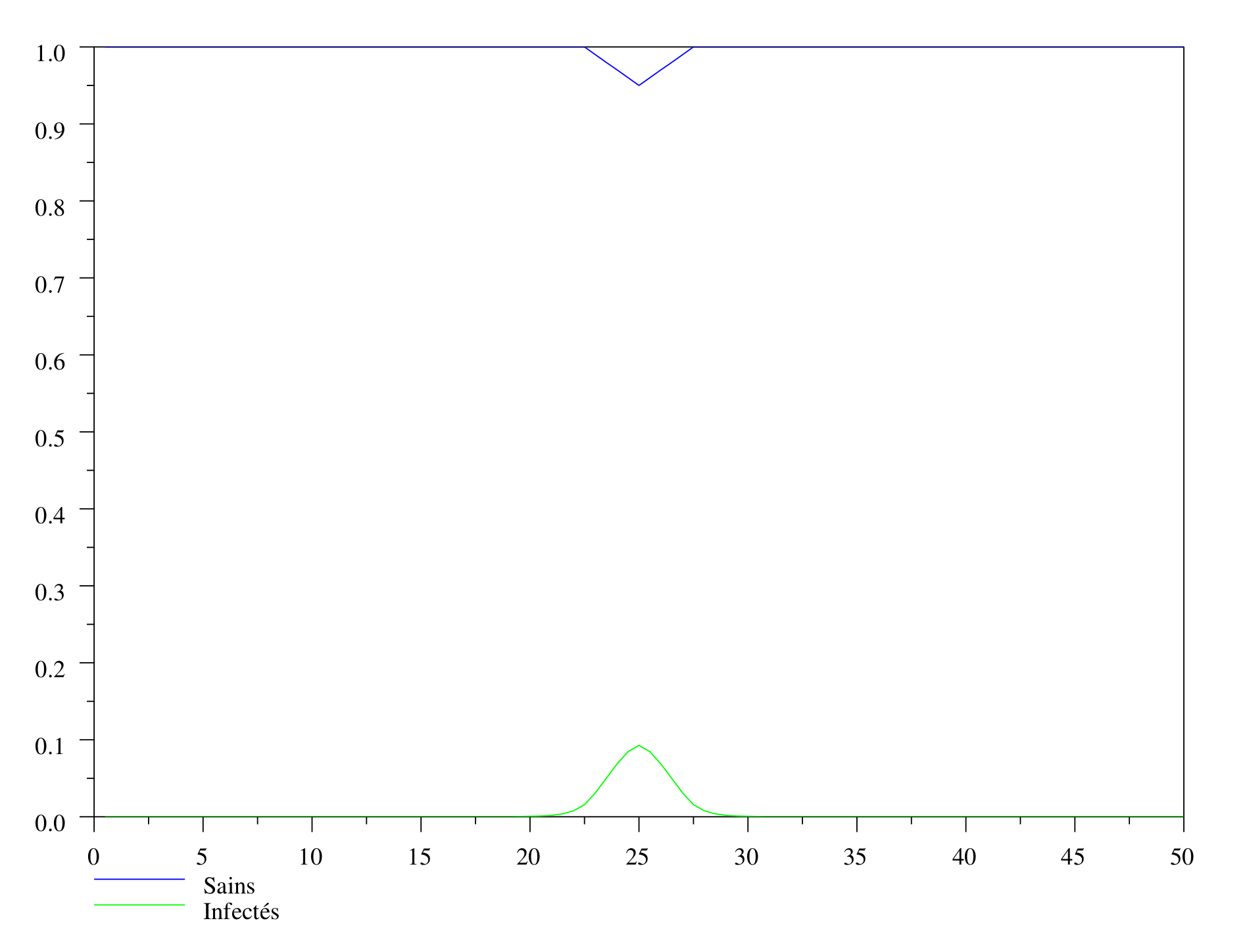
Supposons qu'au départ, on est en présence d'une zone saine ($S=1$), dans laquelle on introduit localement une faible quantité de renards contaminés ($I > 0$ sur une zone géographique réduite, $I=0$ ailleurs). La simulation qui suit a été réalisée grâce au programme RAGE (version matlab ou scilab). La courbe verte représente la population infectée tandis que la bleue représente les individus sains. En accord avec la discussion qui précède, on pourra observer la courbe verte de la population infectée « glisser » peu à peu vers les zones où il y a beaucoup d'individus sains, c'est-à-dire vers les zones où la courbe bleue est élevée.
Au départ, la population saine n’est contaminée qu’à l’endroit précis où a été introduit l’échantillon de renards malades.
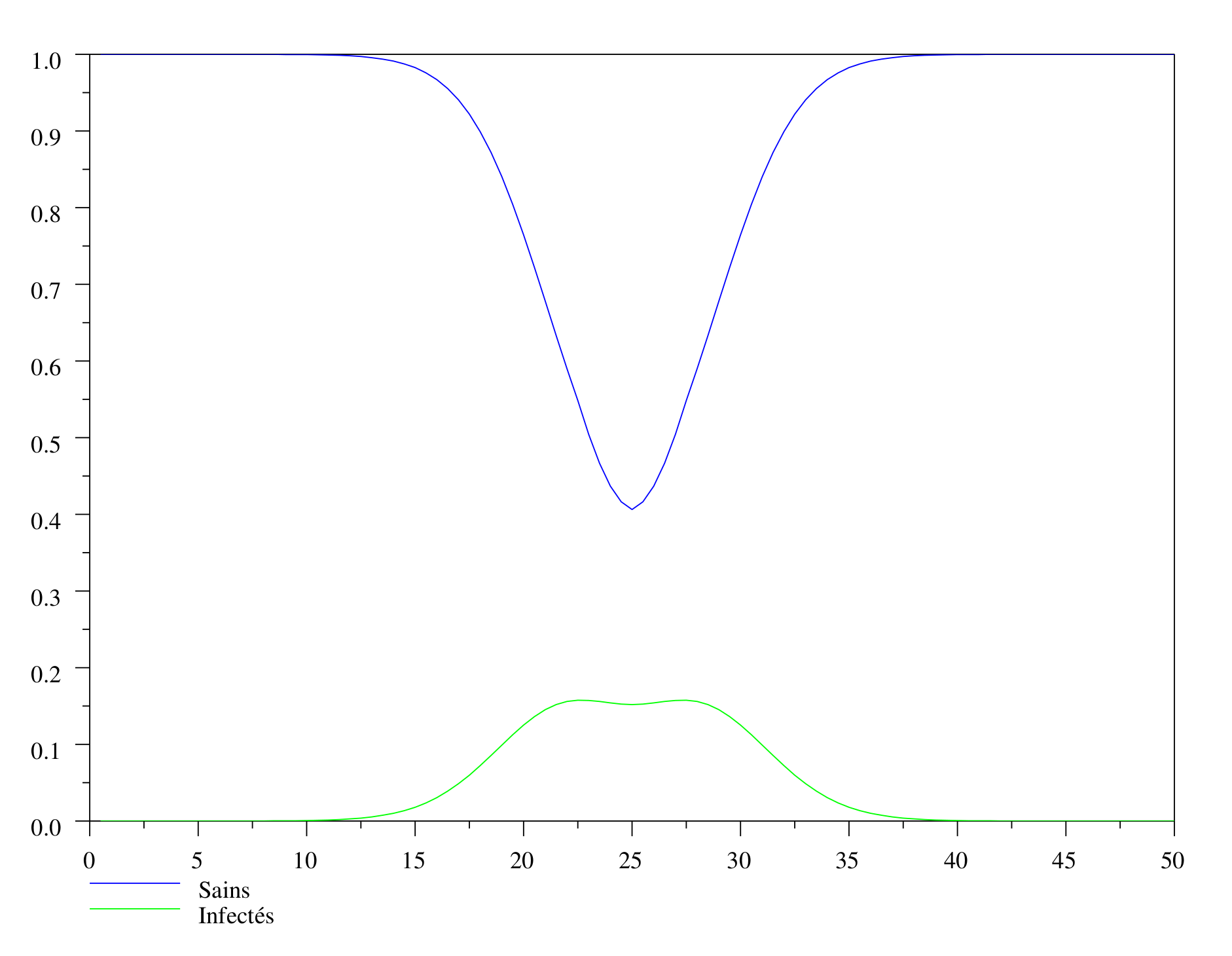
La contamination s’est amplifiée, et l’on voit apparaître deux départs de front : la population infectée a commencé à diffuser. Quant à la population malade au centre, elle commence à décroître : il n’y a pas assez d’individus à contaminer pour compenser la mortalité.
Ce phénomène continue : au centre, l’épidémie est quasiment terminée. Les deux fronts se déplacent peu à peu vers les zones encore non infectées, où la population saine est encore importante.
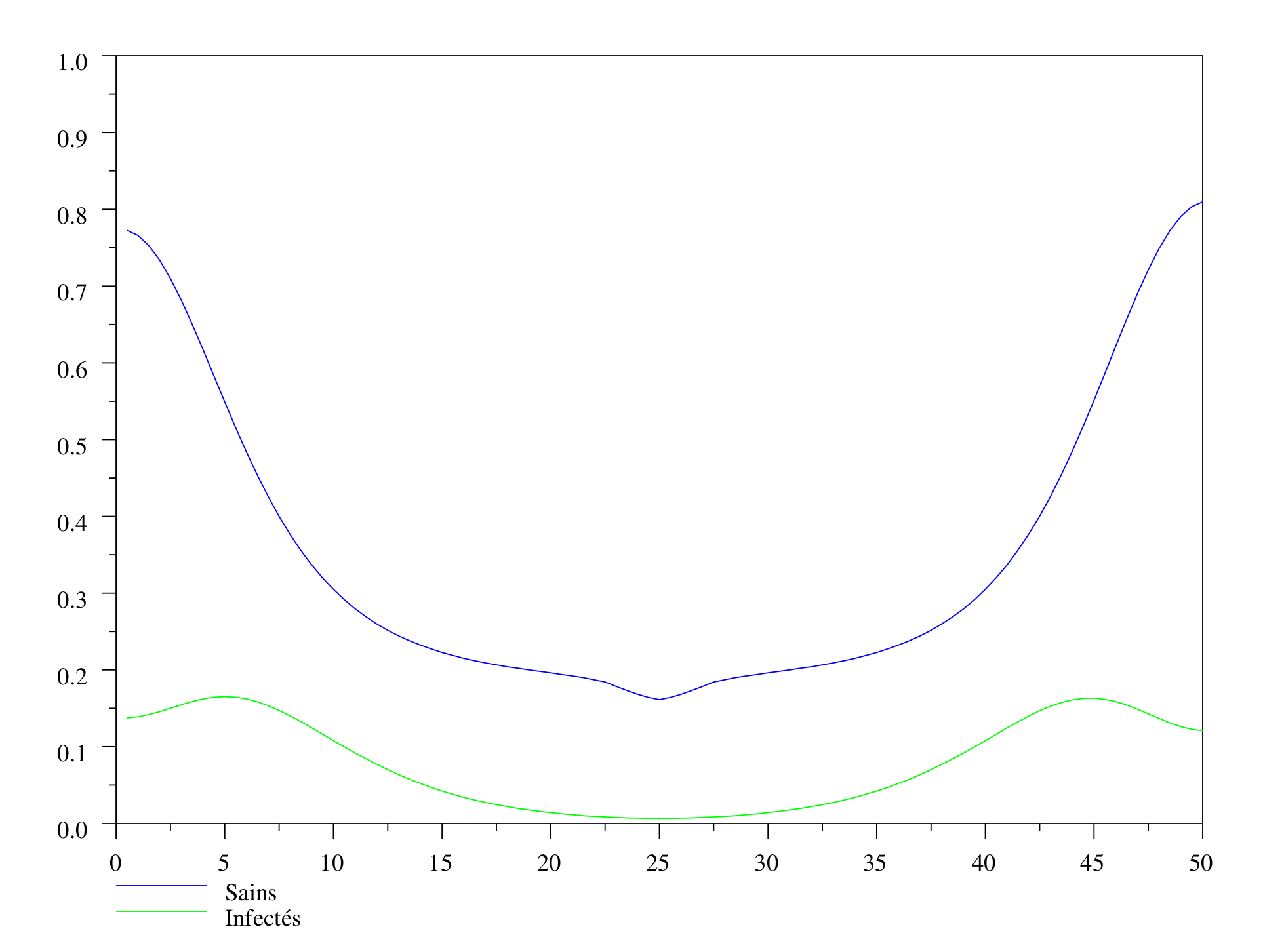
On voit distinctement deux fronts qui s'éloignent du centre où l'épidémie est quasiment terminée.
Les deux fronts sont passés. La population restante et saine est presque la même partout, sauf à l’endroit où l’épidémie a commencée.
Les simulations précédentes mettent en évidence l'existence de fronts de propagation qui s'éloignent de part et d'autre du foyer initial de l'épidémie. Ces objets peuvent être définis précisément d'un point de vue mathématique comme nous allons le voir maintenant.
Ondes progressives
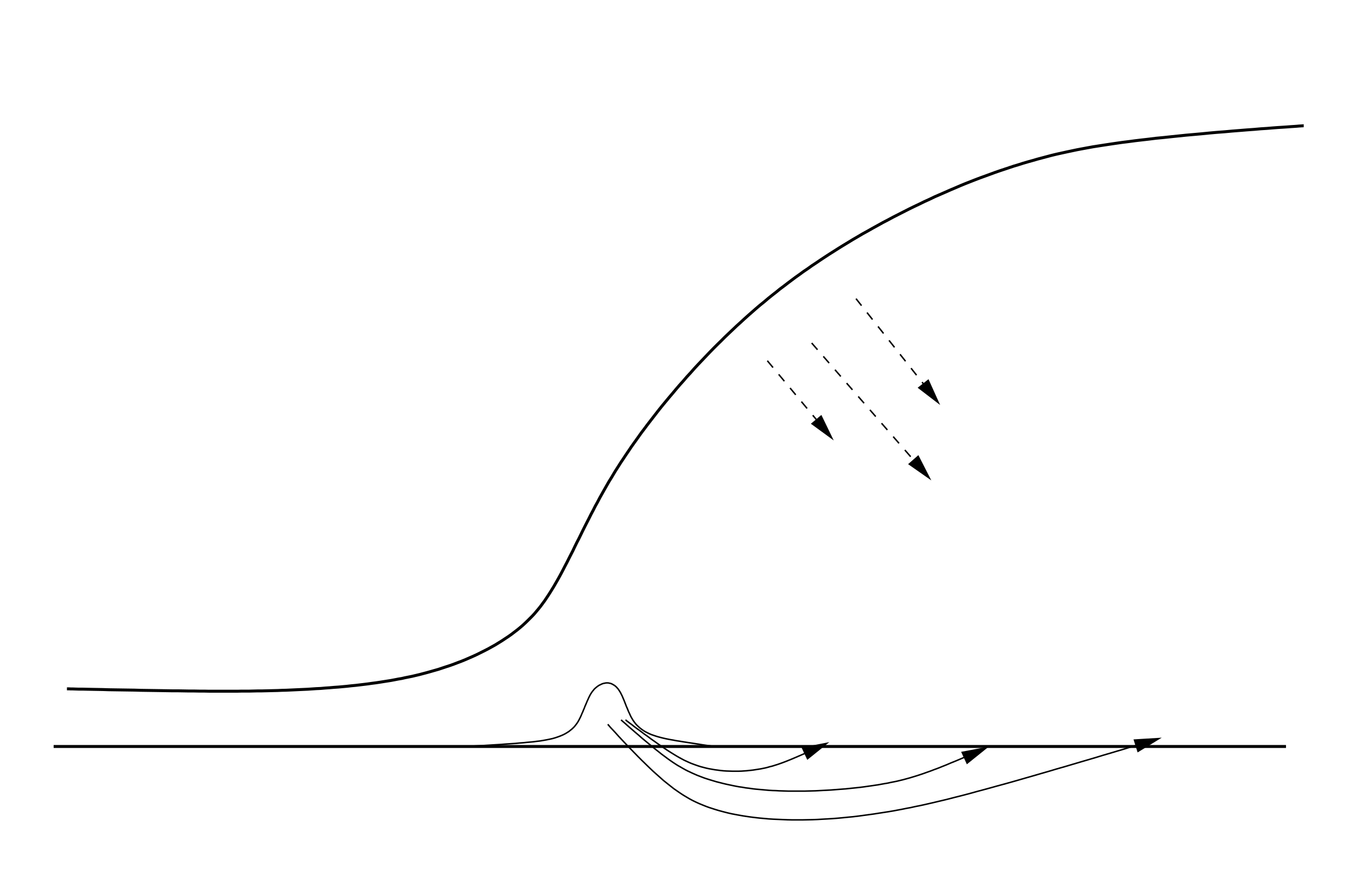
On vient d'observer dans les simulations précédentes que des phénomènes d'ondes apparaissent. À tel point qu'à la fin du phénomène, à part à l'endroit précis où l'on avait introduit une population infectée, la population restante est presque uniforme. C'est à peu de choses près comme si en chaque endroit s'était produit exactement le même phénomène, commençant plus ou moins tôt en fonction de la distance à la zone perturbée.
Enfin, les deux fronts d'onde semblent se propager linéairement par rapport au temps. D'où l'idée de rechercher des solutions du système différentiel sous la forme d'« ondes progressives », c'est-à-dire deux fonctions $S(z)$ et $I(z)$, où $z$ est une nouvelle variable définie par $z = x - c t$ et $c$ est une vitesse à déterminer.
Qualitativement, ceci revient à considérer un repère mobile, qui avance avec le front d'onde à la vitesse $c$. Pour qu'une solution de cette forme corresponde à ce que l'on observe, on demandera également qu'elle vérifie des conditions aux limites de la forme suivante
$$\left\{ \begin{array}{ll} \displaystyle \lim_{z \to +\infty} S (z) = 1 & \text{(avant la passage du front de l'épidémie),} \\ \displaystyle \lim_{z\to+ \infty} I (z)=\lim_{z\to- \infty} I (z) = 0 & \text{(avant et après le front),}\\ \displaystyle \lim_{z \to -\infty} S (z) = 0 & \text{(la population est stable après l'épidémie).} \end{array} \right.$$
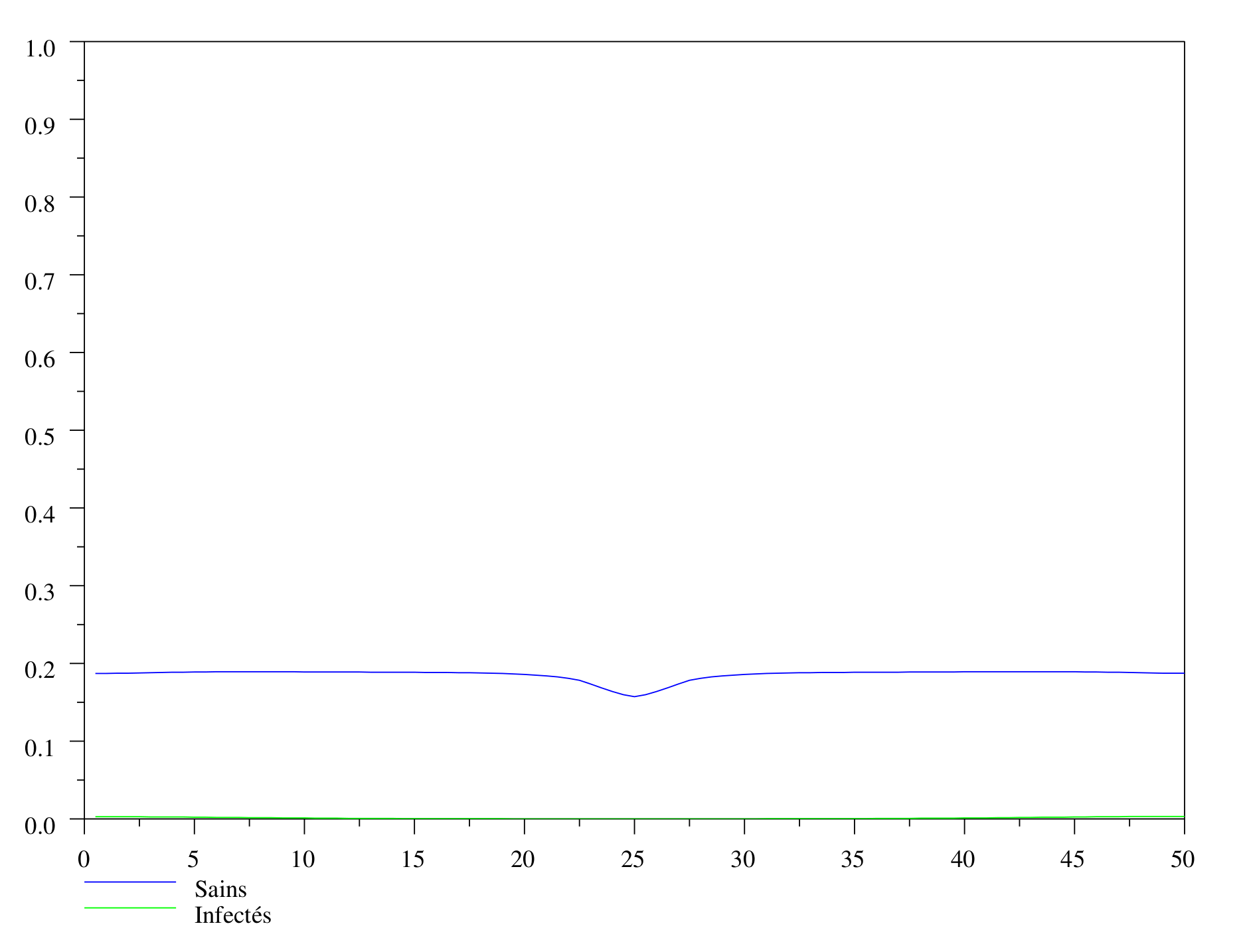
Si l'on recherche une solution sous forme d'onde progressive, on s'aperçoit que celle-ci doit être solution d'un système d'équations différentielles :
$$ \left\{ \begin{array}{l} -c S' = -rIS, \\ -c I' = rIS -\alpha I + D I''. \end{array} \right. $$Là encore, on peut chercher à calculer des solutions approchées sous forme d'ondes progressives, et les vitesses de propagation approchées correspondantes. Le programme RAGE4 (version matlab ou scilab) trace le graphique de la solution, recentrée à chaque pas de calcul à partir du moment où elle tend vers une onde progressive. On s'aperçoit que le tracé se stabilise assez rapidement.
Des modèles plus évolués
On peut améliorer le modèle précédent pour mieux coller à la réalité. Parmi les améliorations possibles, l'une des plus naturelles est de rajouter un terme dit logistique : la population à tendance à croître naturellement, dans la limite des ressources (ou capacités nourricières) du milieu. On rajoute alors un terme de croissance en $B S (1 - S/S_0)$, c'est-à-dire que la population à tendance à croître tant qu'elle est en dessous d'un seuil $S_0$.
À un instant donné, lorsque la population est en dessous de son seuil $S_0$, cette croissance est proportionnelle à la population : le coefficient de proportionnalité n'est autre que le taux de natalité, ou plus exactement le taux de natalité moins le taux de mortalité « naturelle », c'est-à-dire pour d'autres raisons que la rage. L'hypothèse faite ici est que ce taux est de la forme $B (1 - S/S_0)$ : il y a une régulation naturelle de la population, dont le taux de natalité baisse (ou le taux de mortalité augmente, faute de nourriture, de place etc) lorsque la population totale se rapproche du seuil $S_0$, quantité maximale pouvant vivre dans les conditions du milieu.
$$\left\{ \begin{array}{l} \frac{\partial S}{\partial t} = -r IS + B S(1-\frac{S}{S_0}) \\ \frac{\partial I}{\partial t} = r IS - \alpha I + D \Delta I. \end{array} \right.$$
Dans le système précédent, $B$ est une constante qui dépend de l'espèce, c'est elle qui régule la vitesse des variations logistiques. Elle peut dépendre de nombreux facteurs, dont la vitesse de reproduction de l'espèce etc.
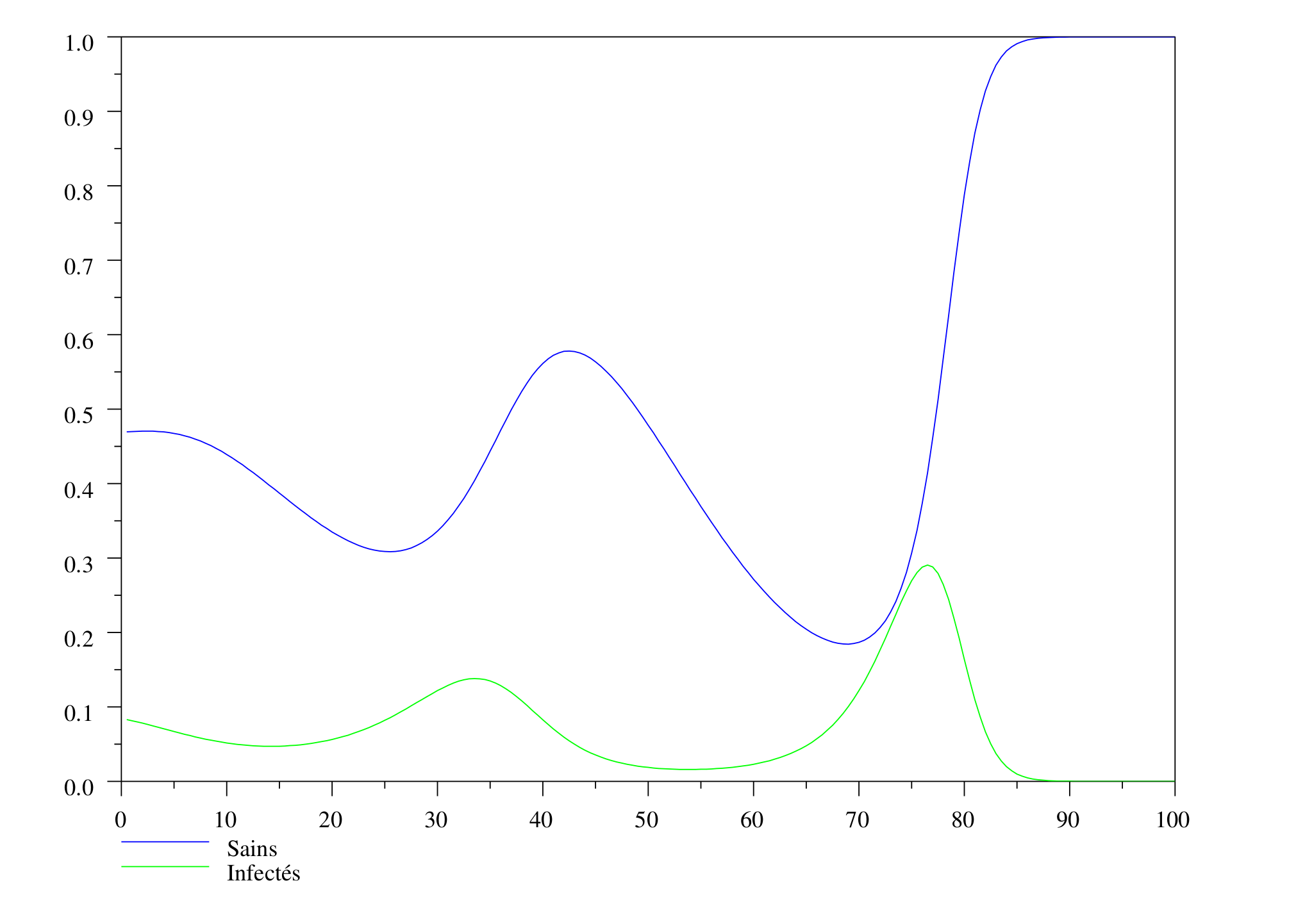
Avec l'introduction de ce nouveau terme, on observe le phénomène nouveau suivant : le nombre de renard réaugmente après le passage de l'épidémie, ce qui donne lieu à des épidémies « secondaires ». On observe également que ces ondes sont de plus faibles amplitudes. En effet, dès que la population a réaugmenté, elle peut être infectée à nouveau s'il reste quelques individus contaminant. Et l'ampleur de la « réplique » dépend surtout du niveau auquel est revenu la population. L'onde progressive, dans ce modèle, a une allure du type :
Ce graphique a été réalisé avec le programme RAGE5 (version matlab ou scilab), qui est presque le même que RAGE4, au terme logistique près.
Ce modèle est assez réaliste : on a pu en observer de nombreuses manifestations. La plus célèbre est l'épisode de la peste noire au 14ème siècle : l'épidémie commence à Gênes en décembre 1347, et se propage dans toute l'europe à une vitesse assez régulière, de l'ordre de 300 à 600 kilomètres par an, tuant au passage un bon tiers de la population. Cette vague fut suivie de nombreuses répliques de moindre ampleur, espacées de quelques années. La première se déclarait en Allemagne en 1356.
Les programmes en matlab et scilab (dans leurs versions de 2004) présentés dans ce texte
- SIR : système d'équations différentielles (matlab / scilab)
- RAGE : modèle SIR avec diffusion et localisation initiale en espace (matlab / scilab)
- RAGE4 : ondes progressives pour le modèle avec diffusion (matlab / scilab)
- RAGE5 : ondes progressives avec diffusion et terme logistique (matlab / scilab)