Toute la puissance du second degré.
Les fonctions du second degré sont introduites en classe de seconde 1. Leur étude se poursuit en classe de première 234 et vise plusieurs objectifs. Un premier est structurel, posant une première pierre à l'édifice de l'algèbre des polynômes et de ses équations. Un deuxième est scientifique, jetant des ponts vers la physique, la chimie ou encore la biologie. Un troisième est économique, touchant à l'optimisation. Un quatrième est culturel, invitant à voyager, à travers les âges, entre l'Orient et l'Occident. Un autre intérêt, pragmatique, voire philosophique, est de nous rappeler que parfois dans la vie, tout n'est pas ... linéaire ! L'éventail des situations, très simples, sélectionnées ici en donne un aperçu, lequel pourra servir aux lycéens d'activités d'accueil, d'amorce ou d'approfondissement.
1) De la logique avant toute chose $\rightleftharpoons$ Structures et logique
Soit l'application $f$ du second degré définie de $\mathbb{R}$ dans lui-même par \[f(x) = ax^2 + bx +c\] où $a$, $b$, $c$ sont des réels, $a$ non nul.
A-t-on:
a) $f$ est paire $\Leftrightarrow$ $b=0$ ?
b) L'image par $f$ de tout entier relatif est un entier relatif $\Leftrightarrow$ les coefficients $a$, $b$, $c$ sont des entiers relatifs ?
c) L'image par $f$ de tout nombre rationnel est un nombre rationnel $\Leftrightarrow$ les coefficients $a$, $b$, $c$ sont des nombres rationnels ?
Les compétences – « Raisonner » – « Calculer » – « Communiquer » ont ici toutes été sollicitées. Nous croiserons la compétence « Modéliser » dès l'exercice suivant, et la compétence « Représenter » sera abondamment travaillée aux exercices 10 et 11.
2) Minimiser une puissance $\rightleftharpoons$ Sciences / Économie
On découpe une ligne chauffante résistive en deux lignes, que l'on rebranche en parallèle sur la tension d'alimentation comme en figure 1. À quel endroit effectuer la coupe pour minimiser la puissance totale dissipée par le nouveau circuit ? On rappelle que la puissance dissipée par une résistance $R$ soumise à une tension $V$ vaut $\frac{V^2}{R}$.
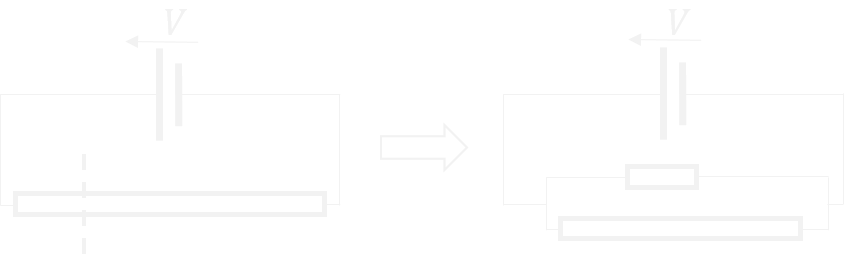
Soit $R$ la résistance de la ligne initiale. La somme des résistances des deux nouvelles lignes valant $R$, celle de la première vaut, mettons, $\frac{R}{2}+x$ et celle de la seconde, $\frac{R}{2}-x$ où $x \in \left[\,0\,;\,\frac{R}{2}\right[$. La puissance totale dissipée est égale à \[ \begin{align*} \mathscr{P}&=\frac{V^2}{\left(\frac{R}{2}+x\right)}+\frac{V^2}{\left(\frac{R}{2}-x\right)}\\ &=\frac{4RV^2}{R^2-4x^2}\end{align*}\]
Cette puissance est minimale quand $x=0$, donc quand la ligne résistive est sectionnée en son milieu.
3) Maximiser un chiffre d'affaire $\rightleftharpoons$ Économie
Un magazine local vendu $9,30$ € l'unité est tiré à $2\;400$ exemplaires. On estime que chaque augmentation de $10$ centimes du prix au numéro fait perdre $20$ acheteurs. Quel prix au numéro doit fixer le vendeur pour maximiser le total des ventes en euro ?
Notons $x$ l'augmentation en dizaine de centimes d’euro. Le montant des ventes en euro, modulé par $x$, vaut \[ (2\;400 -20x)\left(9,3 + \frac{x}{10}\right)\] dont la forme développée, \[ 22\;320 +54x-2x^2\] est maximale en $x = 13,5$ (et nulle notamment en $x = -93$, ce qui a le don de rassurer). Soit un prix au numéro de $10,65$ € pour un tirage de $2\;130$ unités et une vente totale de $22\;684$ € : tel est le meilleur compromis.
4) Partager un trésor $\rightleftharpoons$ Économie / Philosophie
Un groupe d'amis trouve un trésor d'une valeur de $2$ millions, qu'ils partagent équitablement. L'un d'eux déclare: « si nous avions été cinq de moins, j'aurais présentement empoché $20\;000$ de plus ». Combien sont-ils ?
Notons $n$ le nombre d'amis. Les partages étant supposés toujours équitables, que le groupe soit complet ou diminué de $5$ de ses membres, la déclaration de l'un d'entre eux une fois mise en équation s'écrit \[ \frac{2\;000\;000}{n}+20\;000 = \frac{2\;000\;000}{n-5}\] En simplifiant, \[ \frac{100}{n}+1 = \frac{100}{n-5}\] puis en mettant à dénominateur commun, \[ n^2-5n-500=0 \] Soit $n=-20$ (solution négative à rejeter) ou, en définitive, $n=25$. Les amis sont au nombre de $25$.
Dans la mesure où l'on recherchait ici une solution entière, un balayage méticuleux sur, mettons, les cent premiers entiers permettait aussi de conclure.
Question subsidiaire : tous calculs faits, le groupe pourra-t-il vraiment rester amis ? Toujours est-il que, désormais fortunés, l'exercice qui suit est fait pour eux.
5) My teacher is (not) rich $\rightleftharpoons$ Vie courante / Géométrie
On dispose côte à côte horizontalement et verticalement deux cartes de crédit. Essayez vous aussi... les trois coins seront alignés comme en figure 2. En rapportant la largeur à l'unité, quel coefficient $x$ les banquiers ont-ils donc pu choisir ?

Les bords ad-hoc étant parallèles, le théorème de Thalès impose au tout d'être au grand côté ce que le grand côté est au petit, soit \[ \frac{x+1}x = \frac x1 \] étant entendu que, pour des questions matérielles, $x>0$. Après mise à dénominateur commun, l'inconnue $x$ vérifie donc l'équation de Fibonacci5 (dite aussi « équation dorée ») \[ x^2-x-1 = 0 \] Ceci fournit \[ x = \frac{1+\sqrt{5}}{2} = \varphi\quad \text{ (le « Nombre d'Or »)}\quad \text{ ou }\quad x = \frac{1-\sqrt{5}}{2}<0. \] Comme $x>0$, $x=\varphi$. Les proportions d'une carte de crédit sont dorées. Est-ce une allusion aux lingots que les banques espéreraient voir dormir sur nos comptes ?
6) Il n'y a pas de fonction « presque » exponentielle $\rightleftharpoons$ Culture
Déterminer les applications $f$ de $\mathbb{R}$ dans $\mathbb{R}$ vérifiant pour $x$ et $y$ réels \[f(x+y)=f(x)f(y)-1\]
Les équations fonctionnelles ont connu leur heure de gloire dans les programmes de lycée, dont elles n'ont cependant pas totalement disparu, au titre d'approfondissement possible en terminale 1. Bien sûr, elles inspirent encore les compétitions mathématiques, les Olympiades en tête. Nous sommes ici partis de l'une des plus emblématique d'entre elles, puis nous l'avons légèrement perturbée à l'aide d'une constante.
En fixant d'abord $x$ et $y$ à $0$, on trouve $f(0)=f(0)^2-1$. Le réel $X=f(0)$ vérifie l'équation de Fibonacci : \[ X^2-X-1 = 0\] D'où \[ f(0) = \frac{1+\sqrt{5}}{2} = \varphi\quad \text{ ou }\quad X = \frac{1-\sqrt{5}}{2}=1-\varphi=-\frac{1}{\varphi}\] Puis en posant juste $y=0$ il vient après factorisation \[(f(0)-1)f(x)=1\]
De deux choses l'une :
- lorsque $f(0)=\varphi$, $f(x)$ vaut invariablement $\dfrac{1}{\varphi-1}=\varphi$,
- lorsque $f(0)= 1-\varphi$, $f(x)$ vaut invariablement $\dfrac{1}{-\varphi}=1-\varphi$.
Bref, $f$ est soit la fonction constante égale à $\varphi$, soit la fonction constante égale à $1-\varphi$. Et ces deux solutions conviennent.
Plus généralement, on pourrait considérer l'équation fonctionnelle \[f(x+y)=f(x)f(y)-\varepsilon \] où $\varepsilon>0$. De manière analogue, $f(0) = \alpha$ ou $f(0)=\beta$ avec $\alpha+\beta = 1$ et $\alpha\,\beta = -\varepsilon$ (en particulier, ni $\alpha$ ni $\beta$ ne sont nuls). Dans le premier cas, $(\alpha-1)f(x)= -\alpha\,\beta$ donc $f(x)=\alpha$ après simplification, tandis que dans le second $f(x)= \beta$. Ces solutions ne passent pas à la limite quand $\varepsilon \rightarrow 0$. Elles tendent l'une vers $1$ l'autre vers $0$ quand l'équation fonctionnelle débouche sur des exponentielles (quitte à renforcer les hypothèses sur $f$, de continuité par exemple).
7) Une équation de Fermat d'exposant réel $\rightleftharpoons$ Culture
Résoudre l’équation d’inconnue l'exposant $x$ réel \[16^x + 20^x = 25^x\]
Factoriser $16$, $20$ et $25$ mène à \[ 4^{2x} + 4^x 5^x = 5^{2x} \] puis, après avoir posé $X = \left(\frac{5}{4}\right)^x$, à l'équation de Fibonacci \[ X^2-X-1 = 0\] Ceci fournit \[ X = \frac{1+\sqrt{5}}{2} = \varphi \quad \text{ ou } \quad X = \frac{1-\sqrt{5}}{2}=1-\varphi\] Mais la positivité de $X$ écarte la seconde option. Si bien que le problème n'admet qu'une solution \[x = \frac{\log(\varphi)}{\log\left(\frac{5}{4}\right)}\simeq 2,156\] Que cette dernière ne soit pas entière était prévisible au regard du problème de Fermat, lequel exclut d'office $x=3$, $x=4$, $x=5$, etc. Quant aux valeurs particulières $x=0$, $x=1$, $x=2$, une rapide vérification prouve qu'elles ne conviennent pas.
Qu'il existe une solution intermédiaire à $2$ et $3$ était là aussi attendu, continuité des quantités en jeu oblige dans la mesure où $16^2+20^2 = 656$ est supérieur à $625 = 25^2$ et $16^3 + 20^3 = 12\;096$ est inférieur à $15\;626 = 25^3$.
8) L'urne équitable $\rightleftharpoons$ Philosophie
Une urne contient $6$ boules rouges et $x$ boules blanches, indiscernables au toucher, avec $x\geq 1 $. On tire deux boules simultanément au hasard. Comment choisir $x$ pour qu'il y ait $50\;\%$ de chances que ces deux boules soient de la même couleur ?
Tirer deux boules simultanément avec ses deux mains puis les regarder (en observant, par exemple, celle de gauche en premier) revient à les tirer successivement sans remise. Avec les notations ad-hoc — qui renvoient aux couleurs — et grâce à l'indexation ad-hoc — qui rappelle l'ordre du tirage — la situation nous mène à l'arbre de probabilités suivant:
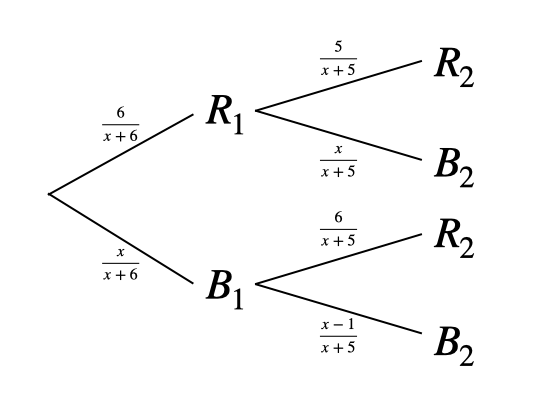
Le problème se traduit ainsi par l'égalité:
\[\mathbb{P}(R_1 \cap R_2)+\mathbb{P}(B_1 \cap B_2)=\frac{1}{2}\] Or, en utilisant les probabilités conditionnelles2 : \begin{align*} \mathbb{P}(R_1 \cap R_2) &= \mathbb{P}(R_1)\;\mathbb{P}(R_2 \mid R_1)\\ &=\frac{6}{6+x}\times \frac{5}{5+x} \end{align*} et, de même, \[ \mathbb{P}(B_1 \cap B_2) = \frac{x}{6+x}\times \frac{x-1}{5+x}\] Aussi l'équation à résoudre devient-elle, après mise au même dénominateur, \[ x^2-13x+30=0\] Ainsi, $x=3$ ou $x=10$. Le jeu est équitable avec $3$ boules blanches ou $10$ boules blanches... mais non $6$, valeur attendue quand on pratique les tirages avec remise.
9) Le problème de l'échelle unique $\rightleftharpoons$ Culture
Une malle cubique de $70$ centimètres de côté est placée contre un mur. On pose, en équilibre sur son couvercle, une échelle de $2,5$ m en contact avec le sol d’un côté, adossée à la paroi de l’autre. Que peut valoir la hauteur d’appui $h$ ?
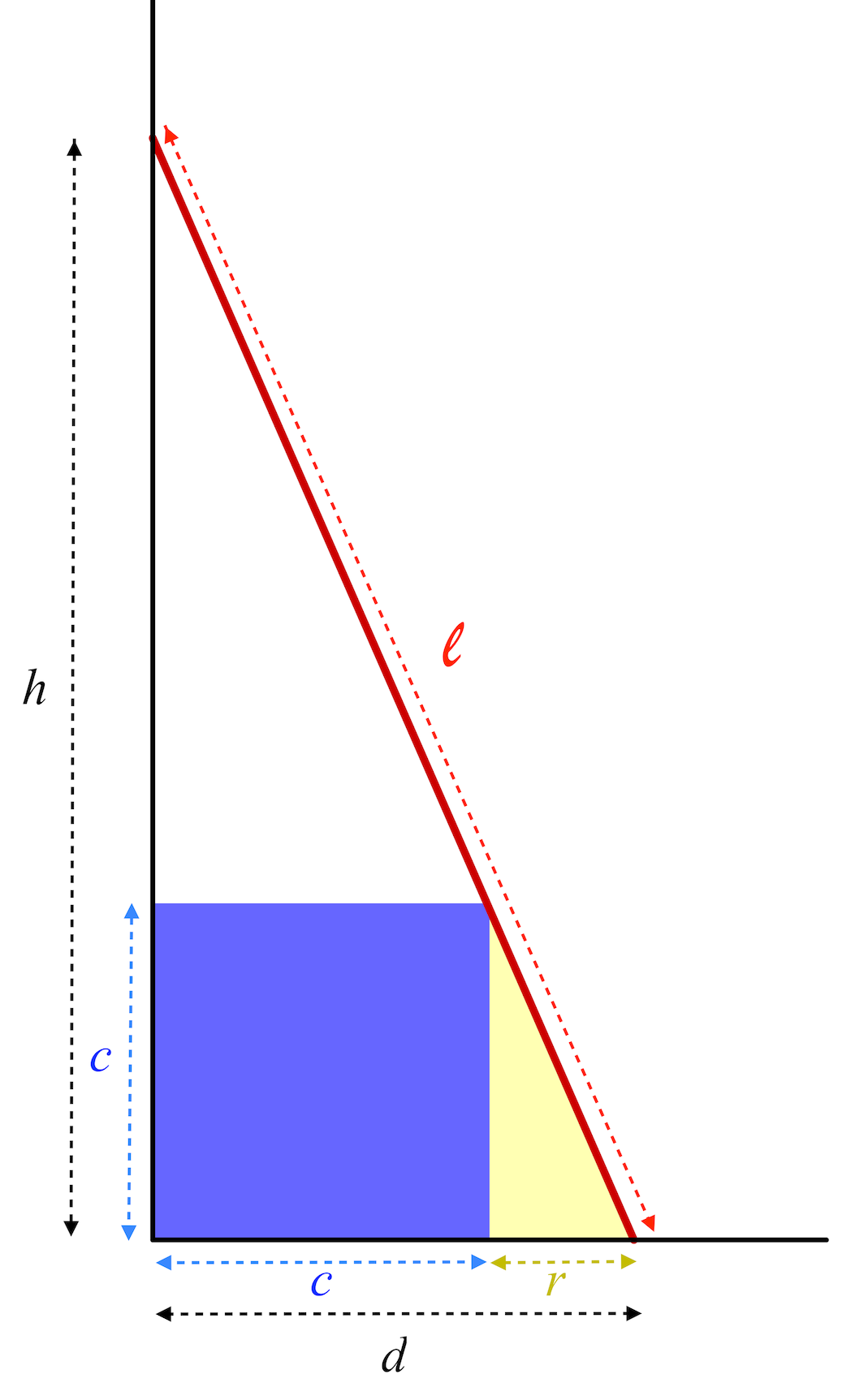
Notons $r$ (respectivement, $d$) le retrait des pieds de l'échelle à la caisse (resp. au mur). Le triangle jaune pâle étant semblable au grand triangle rectangle d'hypoténuse l'échelle toute entière, \[ \frac{r}{d} = \frac{c}{h} \] Comme $c+r = d$, il vient alors \[ \frac{c}{d} + \frac{r}{d}=1 \] puis \begin{equation} \label{eq1} \frac{c}{d}+\frac{c}{h}=1 \end{equation}
Le théorème de Pythagore fournit par ailleurs \begin{equation} \label{eq2} d^2+h^2=\ell^2 \end{equation} Après avoir élevé au carré \eqref{eq1} et combiné avec \eqref{eq2}, on obtient \[ (dh)^2-2c^2 dh-\ell^2 c^2 = 0. \] Les données numériques de l'énoncé, toutes converties en centimètres, conduisent à la seule valeur positive du produit de $d$ par $h$, noté $p$ dans la suite \[ dh = 700(7+\sqrt{674})=p \] puis, connaissant la somme via (\ref{eq1}) \[ d+h = \frac{dh}{c} = \frac{p}{c} \] à deux solutions viables \[ h = \frac{p \pm \sqrt{p^2-19\;600 p}}{140} \] Soit, approximativement, $h \simeq 229$ cm ou $h \simeq 101$ cm, qui correspondent à deux positions symétriques par rapport à la première bissectrice : l'une où l'échelle est pratiquement couchée, l'autre pratiquement debout. Cette énigme, très classique, admet des variantes, en particulier celle dite du « Two Ladders Problem » 34.
10) Usinage de cône $\rightleftharpoons$ Sciences
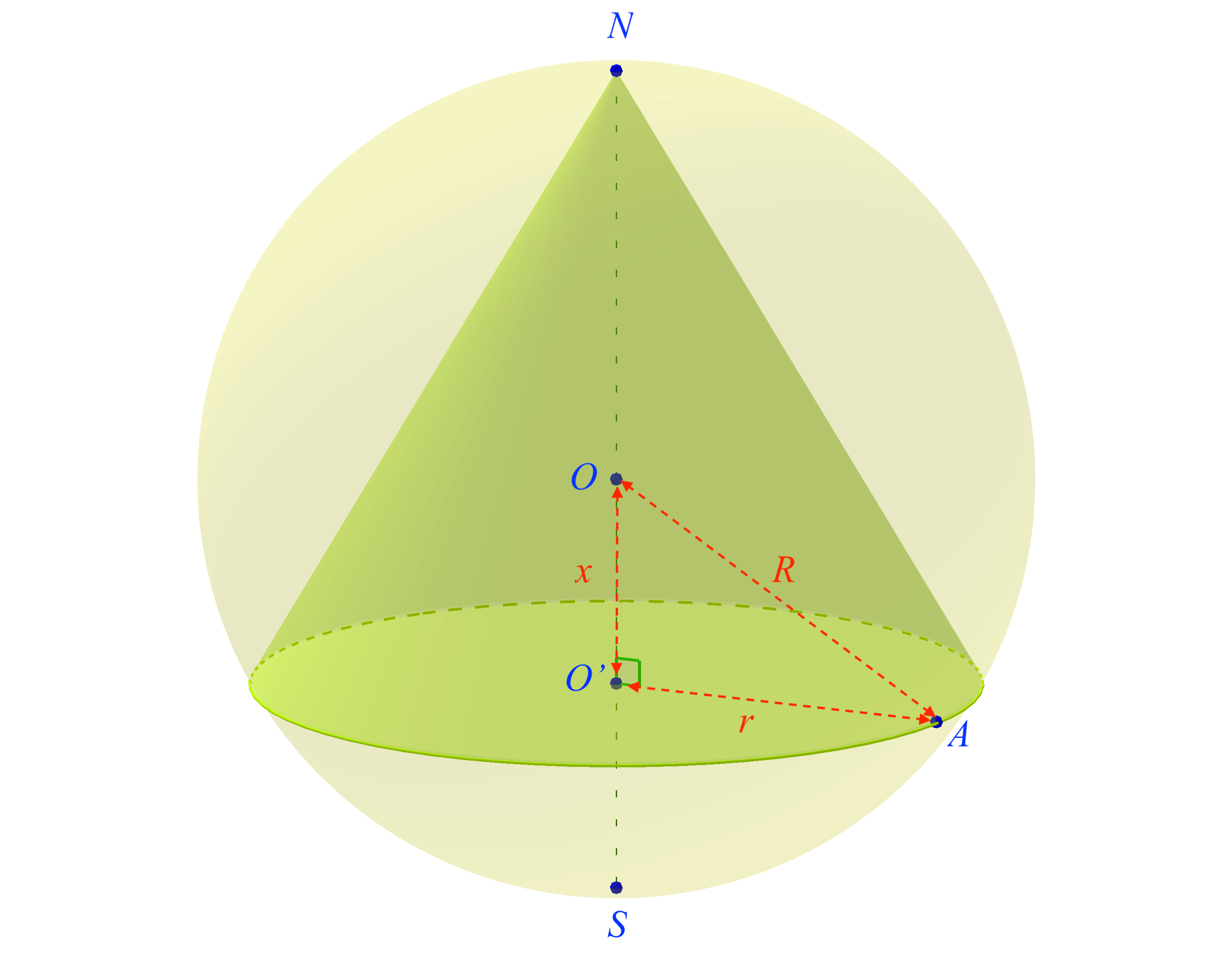
Quel est le plus grand cône de révolution qu'il est possible d'usiner dans une sphère et quel est alors le rapport de leurs volumes ?
Il s'agit donc d'usiner un cône à partir d'une pièce sphérique. Orientons l'axe de la Figure 5 dans le sens de $[0,S)$. Le théorème de Pythagore dans le triangle $OO'A$ rectangle en $O'$ fournit \[r^2=R^2-x^2.\]
Le volume $\mathscr{V}$ du cône est donc, pour $x$ dans $I=[\,-R\, ;\, R\,]$, \[ \mathscr{V}_C(x)=\frac{1}{3}\pi\,r^2\,\times O'N=\frac{1}{3}\pi\, (R^2-x^2)(R+x). \] La dérivation de ce polynôme nous amène alors, pour tout réel $x$ de $I$, à \[\mathscr{V'}_C(x)=-\frac{1}{3}\pi\, (3\,x^2+2\,Rx-R^2) \] dont une racine évidente est $-R$, en périphérie de notre intervalle d'étude. La seconde racine est $\frac{1}{3}R$, en laquelle le volume $\mathscr{V}_C$ atteint son maximum valant: \[ \mathscr{V}_C\left(\frac{1}{3}R\right)=\frac{1}{3}\pi\,\left[R^2-\left(\frac{R}{3}\right)^2\right]\left[R+\frac{R}{3}\right]=\frac{32}{81}\,\pi\,R^3. \]
Le rapport des volumes est alors:
\[
\frac{\frac{32}{81}\,\pi\,R^3}{\frac{4}{3}\,\pi\,R^3}=\frac{32}{81}\times \frac{3}{4}=\left(\frac{2}{3}\right)^3
\]
11) Un flacon de parfum optimal $\rightleftharpoons$ Économie
Un petit flacon de parfum, d'une contenance de $25$ ml, a la forme d'un coin de pavé droit supporté par deux rails rectangulaires fixés sous la base $OAB$, comme sur la Figure 6 ci-après. Les faces $OAC$, $OBC$ et $OAB$ sont peintes, à l'extérieur uniquement, d'une laque coûtant très cher, tandis que la face $ABC$ reste transparente. Les rails, de hauteur $e=2,5$ mm, sont, eux, laqués sur les deux faces et considérés d'épaisseur négligeable. Donner les dimensions du flacon qui coûte le moins cher en peinture.
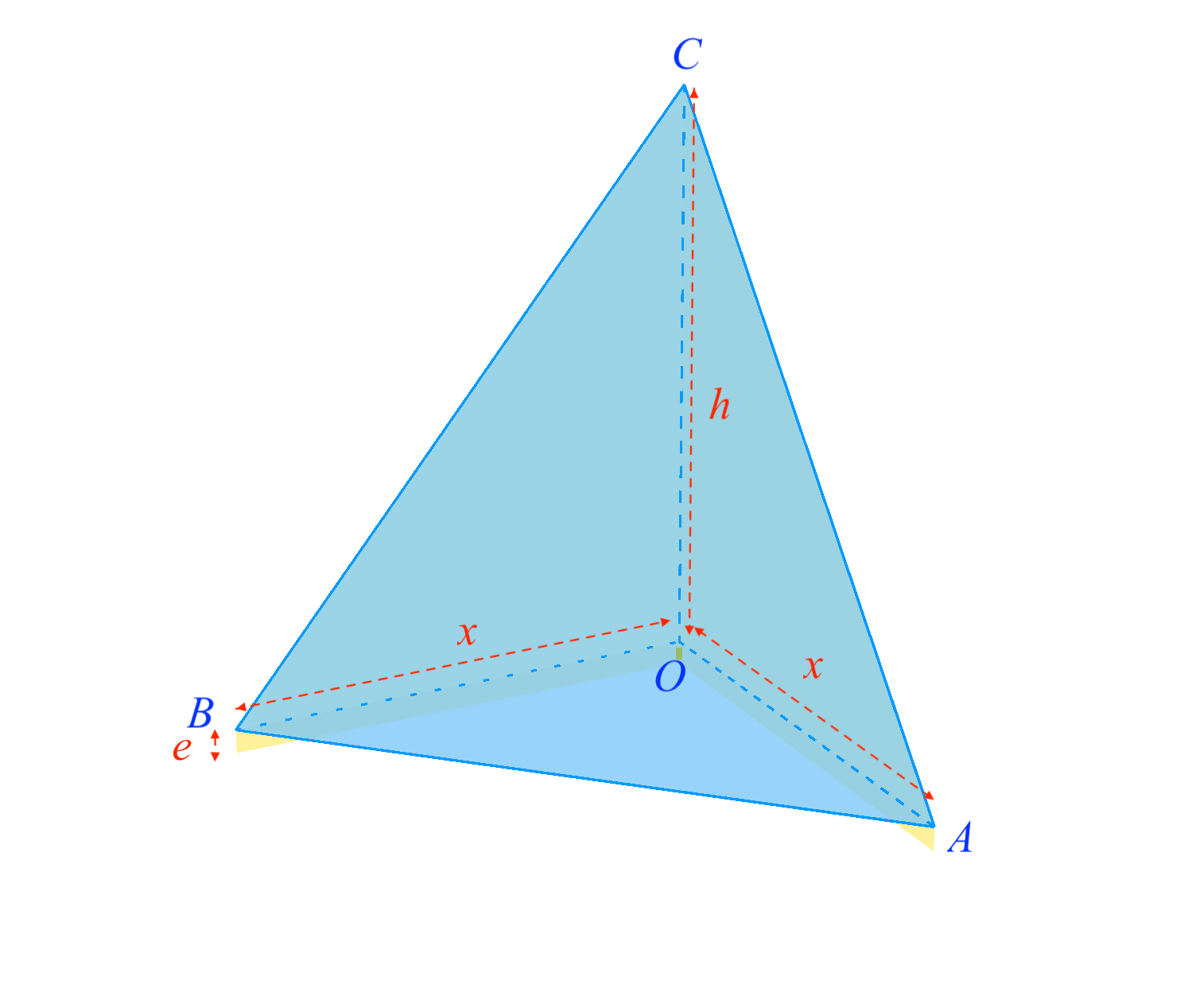
Le volume du tétraèdre est, d'après les notations de la figure cotée, \[\mathscr{V}_T=\frac{1}{3}\times \frac{1}{2}\,x^2\times h. \] Adoptons pour unité le cm : $25 \text{ ml } = 25 \text{ cm}^3$. D'où, pour $x$ réel strictement positif et exprimé en cm, la relation: \[h=\frac{6\;\mathscr{V}_T}{x^2}=\frac{150}{x^2}. \] La surface peinte, composée des trois triangles sur l'extérieur et des deux rails sur leurs deux faces, est alors \[\mathscr{S}=2\left(\frac{1}{2}\,xh\right)+\frac{1}{2}\,x^2+2\times 2\,ex. \] En substituant l'expression de $h$, on obtient \[\mathscr{S}(x)=x\times \frac{150}{x^2}+\frac{1}{2}\,x^2+x=\frac{1}{2}\,x^2+x+\frac{150}{x}. \] La fonction $\mathscr{S}$ se dérive en \[\mathscr{S}'(x)=x+1-\frac{150}{x^2}=\frac{x^3+x^2-150}{x^2}. \] Elle est donc du signe de son numérateur, polynôme de degré $3$ admettant $5$ comme racine évidente, ce qui donne \[\mathscr{S}'(x)=\frac{(x-5)(x^2+6x+30)}{x^2}. \] Le trinôme du second degré obtenu par factorisation est de signe constant, ici strictement positif : soit qu'on remarque que chacun de ses termes l'est soit qu'on en calcule le discriminant (strictement négatif). En conclusion, la surface peinte est minimale pour $x=5$ (cm) et par conséquent $h=6$ (cm).
12) Une propriété de Tchébychev $\rightleftharpoons$ Optimisation / Logique
On souhaite ici prouver que pour toute application $P$ du second degré définie du segment $[\,-1\,;\,1\,]$ dans $\mathbb{R}$ par: \[P(x) = ax^2 + bx +c\] où $a$, $b$, $c$ sont des réels, $a$ non nul, on a $$\max \vert P(x)\vert \geq \frac{\vert a \vert}{2}.$$
a) Vérifier ce résultat pour la fonction polynôme $T$ (dite de Tchébychev) définie sur $[\,-1\,;\,1\,]$ par: $$T(x)=2x^2-1.$$
b) On revient au cas général. Conclure en procédant par l'absurde après avoir envisagé la fonction auxiliaire $\Delta = P - \frac{a}{2}T$.
a) Une étude de la fonction $T$ de Tchébychev1 mène au résultat. Mais il est plus judicieux d'examiner $T(\cos(x))$, qui balaye toutes les valeurs atteintes par $T$ sur $[\;-1\;;\;1\;]$. L'expression se simplifie en $\cos(2x)$, et culmine en valeur absolue à $1 = \frac{\vert a \vert}{2}.$
b) Raisonnons par l'absurde. Supposons la fonction $P$ strictement bornée par $\frac{\vert a \vert}{2}$ sur le segment $[\;-1\;;\;1\;]$. Dès lors, les signes de $\Delta$ alternent en -1, 0 et 1. D'après le théorème des valeurs intermédiaires, $\Delta$ s'annulerait sur $]\;-1\;;\;0\;[$ et de nouveau sur $]\;1\;;\;0\;[$. Or $\Delta$ se simplifie en $\Delta(x)=bx+c$. Affine, la fonction $\Delta$ doit être identiquement nulle sur $[\;-1\;;\;1\;]$. Il y a contradiction puisque, par exemple, $\Delta(-1) \ne 0$.
13) Population de bactéries et processus de Galton-Watson $\rightleftharpoons$ Sciences
Une colonie de bactéries est obtenue par la mise en culture d'une bactérie souche. Chaque heure cette bactérie souche, ainsi que ses descendantes directes et indirectes, meurt avec la probabilité $1-p=\frac{2}{3}$ ou bien se divise avec la probabilité $p=\frac{1}{3}$ comme en figure 3. Le cas échéant, chacune des deux nouvelles branches vit sa vie en toute indépendance. Démontrer que la population totale finit, en toute probabilité, par s'éteindre.
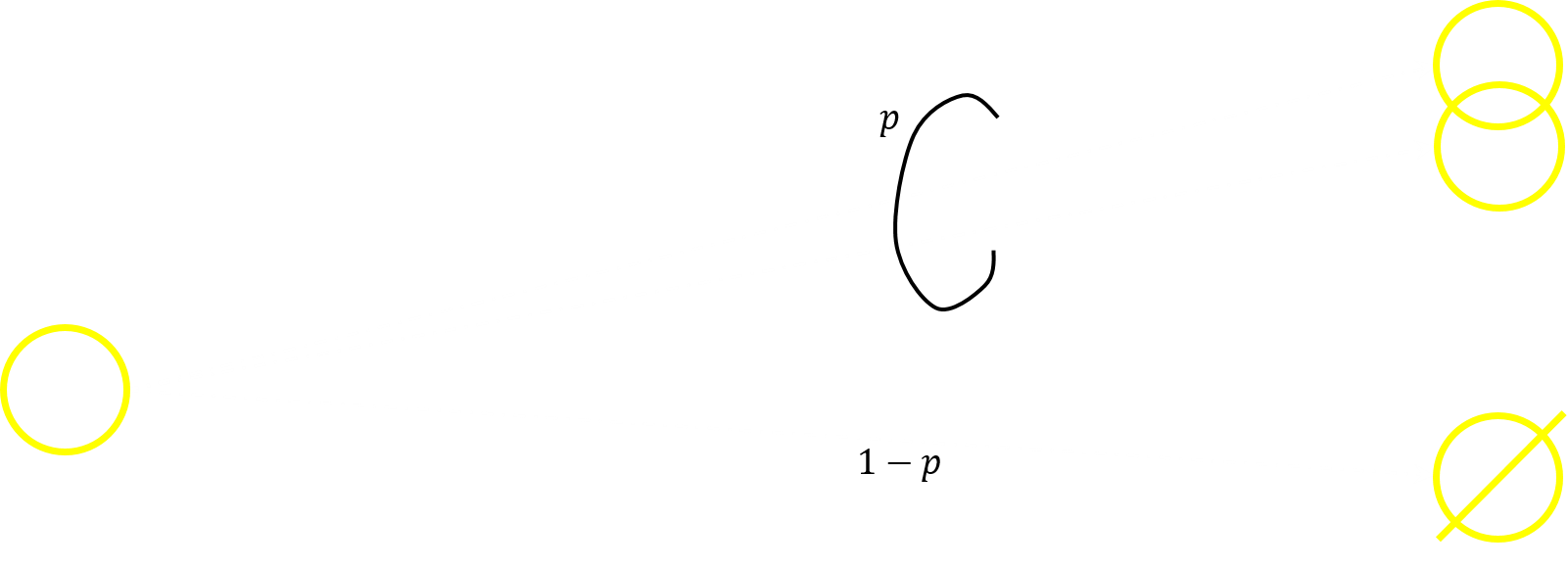
Notons $E$ l'événement : « la colonie finit par s'éteindre », à savoir qu'elle disparaît en un temps fini — ce que nous voulons établir avec la probabilité unité (presque sûrement, donc). Pour ce faire, discutons selon la réalité de la première division cellulaire. Celle-ci nous permettra de conditionner nos calculs. Ainsi, soit la « bactérie souche1 meurt avant de se dédoubler » (Ø)2, soit « elle se dédouble » (ꚙ)3. Si bien que \[\mathbb{P}(E) = \mathbb{P}(E \mid Ø)\; \mathbb{P}(Ø)+\mathbb{P}(E \mid ꚙ)\;\mathbb{P}(ꚙ)\]
Quand d'entrée la bactérie souche meurt, la colonie disparaît : \[ \mathbb{P}(E \mid Ø)=1\] Quand la bactérie souche se dédouble, envisager $\mathbb{P}(E \mid ꚙ)$ revient à envisager deux lignées parallèles nous ramenant chacune, à une translation du temps près, au comportement de la colonie d'origine. Les deux lignées doivent s'éteindre, ce qu'on code par les événements $E_1$ et $E_2$ dont le conditionnement par l'événement ꚙ est implicite.
Ainsi, \[\mathbb{P}(E \mid ꚙ) = \mathbb{P}(E_1 \cap E_2)\] l'indépendance des lignées entraînant \[\mathbb{P}(E \mid ꚙ) = \mathbb{P}(E_1)\;\mathbb{P}(E_2)\] et l'invariance des comportements \[\mathbb{P}(E_1)\;\mathbb{P}(E_2) = \mathbb{P}(E)^2\] D'où l'équation, \[\mathbb{P}(E) = \frac{2}{3}+\frac{\mathbb{P}(E)^2}{3}\] qui n'offre que deux possibles : $\mathbb{P}(E) = 2$, évidemment proscrite en termes de probabilité car supérieure à $1$, et $\mathbb{P}(E)=1$.
On peut se demander ce qu'il advient quand on change la probabilité $p$. Plus généralement, il s'agissait là d'un processus dit de branchement de Galton45.-Watson6, appartenant lui-même à la grande catégorie des chaînes de Markov7.






