Cap vers le Grand oral avec la constante $\gamma$ d'Euler !
En classe de terminale 12, on acquiert déjà un bagage suffisant permettant, en Analyse et en Informatique, de voir quelques pépites. C'est le cas de la somme harmonique. Tout en offrant à l'élève un belvédère vers ce qui pourrait être son premier sommet, la constante $\gamma$ d'Euler, le sujet renferme une vraie richesse, tant historique que scientifique 345. Faisons le point sur la question, sans nous éloigner outre mesure des programmes, par exemple dans l'esprit du Grand oral 6 de mathématiques et de NSI. Ce faisant, nous exploiterons les théorèmes de comparaison, les théorèmes de monotonie, les opérations sur les limites, la logique d'une démonstration par l'absurde, le principe de récursivité et, pour finir en beauté, deux dessins qui vaudront cent discours.
Considérons donc pour tout entier naturel $n\geq1$, $$ H_n = \sum_{k=1}^n \frac{1}{k}. $$ Nous allons successivement nous intéresser à la nature de la suite $(H_n)_n$, à sa limite, puis à son comportement asymptotique.
Nature de la somme harmonique. Chaque rang $n$ permet à $H_n$ d'accumuler un terme supplémentaire et positif. Plus formellement, et pour tout $n\geq 1$, $$ H_{n+1}-H_n = \frac{1}{n+1} \geq 0. $$ Donc la suite croît.
Comme toute suite, $(H_n)_n$ ne fait que converger ou diverger. À supposer qu'elle converge, notons $\ell$ sa limite, alors finie. Considérons la tranche $$ H_{2n}-H_{n} = \sum_{k=n+1}^{2n} \frac{1}{k}. $$ Le membre de droite comporte $n$ nombres, tous supérieurs à $\frac{1}{2n}$. Il est donc supérieur à $\frac{1}{2}$. Ainsi, \begin{equation} \label{inequation} H_{2n}-H_{n}\geq \frac{1}{2}. \end{equation} Le membre de gauche est composé de $H_n$, qui tend vers $\ell$, et de $H_{2n}$, qui y va aussi (plus rapidement, même). D'après les opérations sur les limites, l'ensemble tend vers $\ell-\ell=0$. Si bien qu'un passage de l'inégalité large (\ref{inequation}) à la limite entraîne $$ 0\geq \frac{1}{2}. $$ Par l'absurde, la suite $(H_n)_n$ ne converge pas. Donc elle diverge 7.
Limite de la somme harmonique, ordre de grandeur. La croissance de $(H_n)_n$ précise l'alternative en ces termes : si la suite ne converge pas, c'est quelle diverge vers $+\infty$. Ainsi, $$ \lim_{n \to +\infty} H_n = +\infty. $$ Ouvrons cependant un autre chemin conduisant à ce résultat, avec l'avantage de fournir une idée d'un ordre de grandeur de $H_n$. Pour cela, attachons-nous au nombre de chiffres composant l'écriture décimale de $n$ et, pour mieux comprendre, travaillons d'abord sur un exemple : mettons $n=2\,022$, qui comporte 4 chiffres. Découpons $H_n = H_{2\,022}$ comme suit : $$ H_n = \sum_{k=1}^9 \frac{1}{k} + \sum_{k=10}^{99} \frac{1}{k} + \sum_{k=100}^{999} \frac{1}{k} + \sum_{k=1\,000}^{2\,022} \frac{1}{k}. $$ Analysons :
- La première portion contient $9$ nombres, tous supérieurs au dernier, $\frac{1}{9}$, donc aussi à $\frac{1}{10}$. Elle dépasse alors $9\times \frac{1}{10} = \frac{9}{10}$ ;
- La deuxième portion contient $90$ nombres, tous supérieurs au dernier, $\frac{1}{99}$, donc aussi à $\frac{1}{100}$. Elle dépasse alors $90\times \frac{1}{100} = \frac{9}{10}$ ;
- La troisième portion contient $900$ nombres, tous supérieurs au dernier, $\frac{1}{999}$, donc aussi à $\frac{1}{1\,000}$. Elle dépasse alors $900\times \frac{1}{1\,000} = \frac{9}{10}$ ;
- La quatrième et dernière portion est positive.
Au total, $H_{2\,022} \geq \frac{9}{10} \times 3$. Le raisonnement, tenu ici sur un cas générique, consiste à partitionner les indices de sommation par unités, dizaines, centaines, milliers, etc. Nous obtenons dans le cas général : $$ H_n \geq \frac{9}{10} \times ((\text{nombre de chiffres de }n) - 1). $$ Par comparaison, nous retrouvons $$ \lim_{n \to +\infty} H_n = +\infty. $$ Mieux, nous entrevoyons un rapport possible entre $H_n$ d'une part, et d'autre part le nombre de chiffres de $n$, lequel est de l'ordre de $\log(n)$, lui-même voisin de $\ln(n)$. Le paragraphe suivant va révéler au grand jour cette proximité.
Comportement asymptotique de la somme harmonique. Au vu de ce qui précède, envisageons $H_n - \ln(n)$ ou mieux, c'est à un détail près, plutôt $H_{n-1} - \ln(n)$. Reportons-nous à la figure 1.
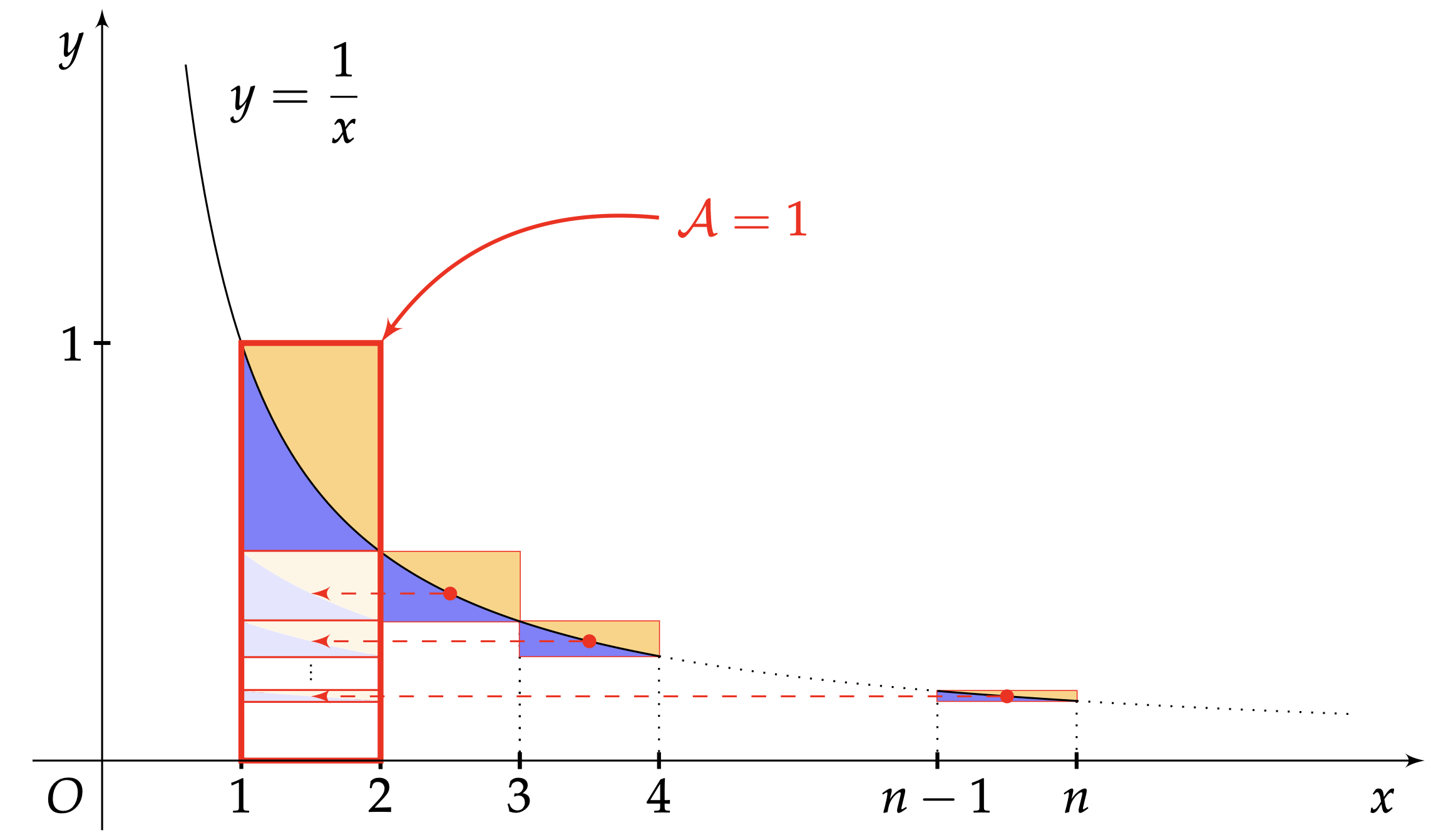
- Interprétons $H_{n-1}$ comme une aire sous un escalier, faite d'aires élémentaires situées sous ses marches. La première marche commence au niveau de l'abscisse 1, la dernière marche commence au niveau de l'abscisse $n-1$ et sa contremarche se situe en l'abscisse $n$.
- Interprétons $\ln(n)$ comme une aire sous une courbe : celle délimitée par la fonction inverse, de l'abscisse 1 à l'abscisse $n$. Soit $$\int_1^n \frac{\text{d}t}{t}.$$ Cette aire se décompose elle-même en aires élémentaires bordées, en abscisse, par des entiers consécutifs via la relation de Chasles ;
- Interprétons donc $H_{n-1} - \ln(n)$ comme une somme de différences de $n-1$ aires élémentaires. Chacune de ces $n-1$ différences revient à une petite aire, comptée positivement, d'une figure qui ressemble à un triangle (peint en orange), en équilibre sur la fonction inverse.
Chaque rang $n$ permet ainsi à $H_{n-1} - \ln(n)$ d'accumuler un pseudo-triangle supplémentaire. Donc la suite $(H_{n-1} - \ln(n))_n$ croît. Montrons qu'elle est majorée. Dans ce but, commençons par majorer l'aire de chaque pseudo-triangle en l'inscrivant dans le rectangle (dessiné en rouge à traits fins) basé sur les mêmes sommets. Les $n-1$ petits rectangles mis en évidence peuvent coulisser horizontalement les uns par rapport aux autres. Glissons-les tous à gauche. Ils rentrent dans la colonne que délimite la plus haute marche (en rouge à traits gras). De ce fait, $$ H_{n-1} - \ln(n) \leq 1. $$ Tous les ingrédients y sont : la suite $(H_{n-1} - \ln(n))_n$ est croissante et majorée. Elle converge donc vers un certain nombre, appelé constante d'Euler et noté $\gamma$. Comme la quantité $H_{n} - \ln(n)$ ne diffère de la quantité $H_{n-1} - \ln(n)$ que d'un terme, $\frac{1}{n}$, elle tend8 elle aussi vers $\gamma$. De plus, les théorèmes de comparaison encadrent cette constante, qui se trouvera entre 0 et 1. Bref : \begin{equation} \sum_{k=1}^n \frac{1}{k} = \ln(n)+\gamma + \varepsilon_n \end{equation} où $\varepsilon_n \to 0$. Une étude plus approfondie mènerait à $$\gamma = 0,577\,215\,664\,901\,532\cdots$$
Mais comment obtenir autant de chiffres après la virgule de $\gamma$ ?
Une première idée, naïve, pour approcher $\gamma$ consiste à traduire le calcul de $H_n$, pour $n$ grand, par une boucle cumulative. Commencer à $1$, ajouter $\frac{1}{2}$, soit sommer $1+\frac{1}{2}$, ajouter $\frac{1}{3}$, soit sommer $(1+\frac{1}{2})+\frac{1}{3}$, ajouter $\frac{1}{4}$ soit sommer $(1+\frac{1}{2}+\frac{1}{3})+\frac{1}{4}$, etc. Enfin, une fois $H_n$ obtenu, retrancher $\ln{n}$. C'est ce que code la fonction Python ci-dessous. On notera que le logarithme népérien y est rendu par la fonction math.log($\cdot$), qui rappelle plutôt un logarithme décimal :
import math
def gamma_imperatif(n):
s = 0
for i in range(n):
s = s + 1/(i+1)
return s − math.log(n)
Avec un processeur arithmétique à double précision, on gagne d'abord une décimale de plus sur $\gamma$ à mesure que $n$ est décuplé, puis on plafonne dès que $n$ avoisine 20 milliards. La précision sur $\gamma$ est alors d'environ $10^{-10}$. Cela tient aux limites de représentation des nombres sur machine, vite atteintes par ce procédé. En effet, pour tout indice $k$, $H_k$ résulte ici de l'addition effective de $H_{k-1}$ et de $\frac{1}{k}$. Quand $k$ est grand, $H_{k-1}$ l'est aussi, tandis que $\frac{1}{k}$ est tout petit. L'ordinateur somme donc deux membres de calibres très différents. La contribution du second est négligée dans l'opération. Les termes $\frac{1}{k+1}$, $\frac{1}{k+2}$, etc. subiront le même sort. Pourtant, s'il en avait été fait masse avant d'effectuer l'arrondi, sans doute auraient-ils été mieux préservés.
Il faut donc envisager le calcul progressif de $H_n$ autrement. De droite à gauche par exemple. Ou, plus subtil, en regroupant les termes constituant $H_n$ de sorte que les additions en jeu ne portent jamais que sur des entités du même ordre. La solution peut tenir en un programme récursif, et non plus impératif, codé par la fonction Python ci-dessous :
import math
def gamma_recursif(debut , fin ):
if debut == fin:
return 1/debut
else:
return gamma_recursif(debut ,math.floor((debut+fin)/2))\
+ gamma_recursif(math.floor((debut+fin)/2)+1, fin)
n = 25000000000 #25 milliards
print(gamma_recursif(1,n) − math.log(n))
Après $n=20$ milliards, la connaissance de $\gamma$ continue de s'apprécier : à $10^{-11}$, puis $10^{-12}$ près même. Pour mieux comprendre, voici en figure 2, quand $n=13$, comment le calcul de $H_{13}$ est traité. De gauche à droite, l'ordinateur partitionne les données en segments contigus, jusqu'à les atomiser. Cette étape achevée, il propage les additions de droite à gauche dans un ruissellement qui ne fait jamais se rencontrer que des affluents de tailles comparables. La précision en est significativement accrue (le temps de calcul et l'occupation mémoire... aussi !).
Bien sûr, il existerait une version impérative de ce nouvel algorithme. Elle sera moins élégante mais s'exécutera plus vite. À vous de jouer !
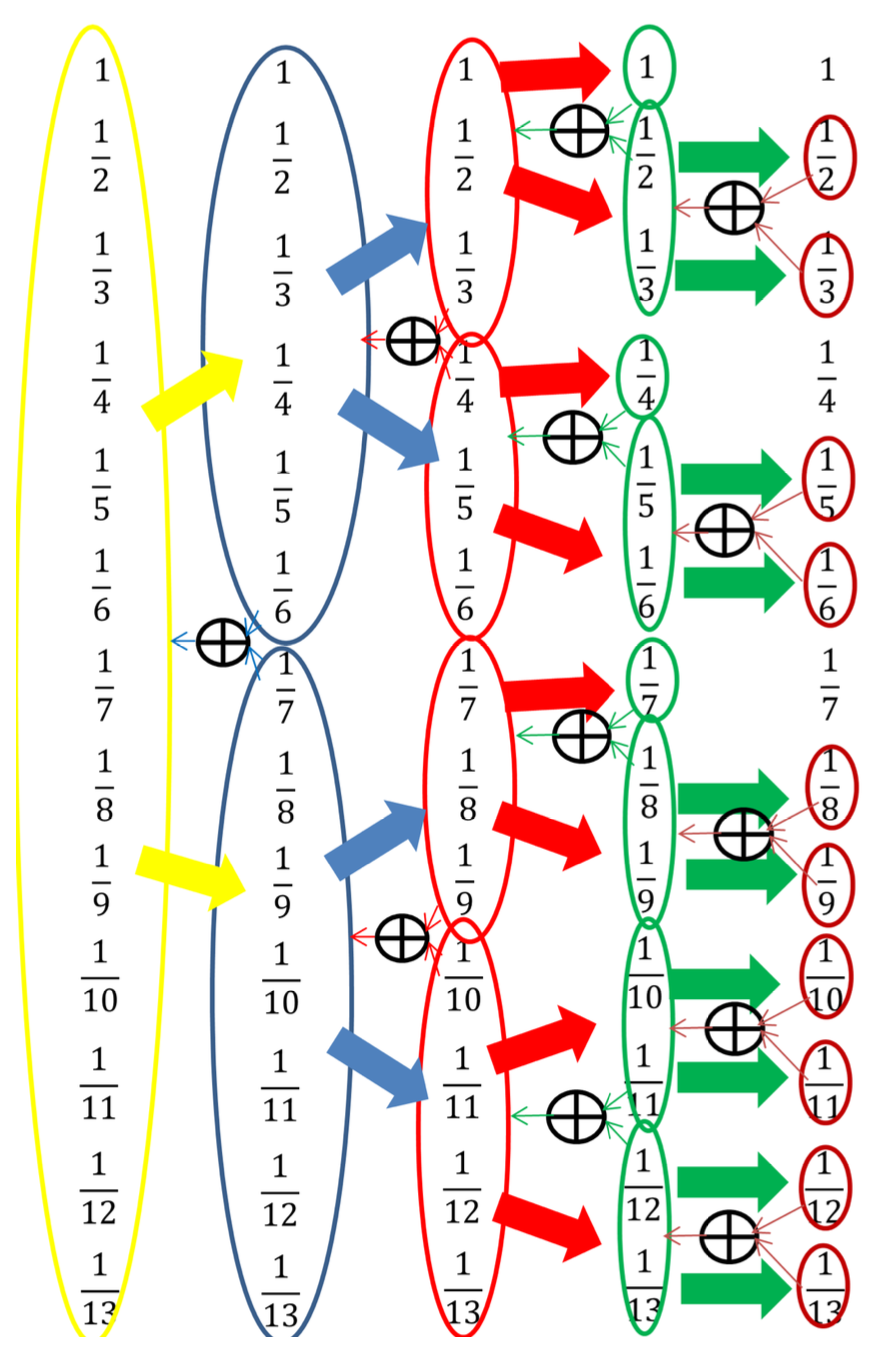
L’algorithme est progressif-rétrogressif. De gauche à droite, les données sont préparées, comme on organiserait le tableau d’un tournoi sportif. De droite à gauche, on en lit les résultats successifs. Ces derniers s’altèrent d’autant moins qu’ils sont appariés entre voisins de mêmes gabarits.







