Entre une théorie des graphes et un parcours d’étude sur les azulejos.
Entre une théorie des graphes, destinée aux enseignants en charge de l’option de mathématiques de la classe de Terminale ES, et un parcours d’étude sur les azulejos, expérimenté entre 2016 et 2018 en cycle 3, l’IREM d’Aix-Marseille présente deux documents pour la formation des professeurs.
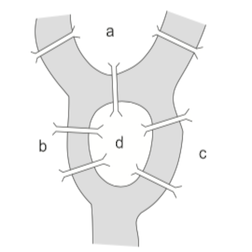
Les ponts de Koenigsberg
Ce problème est posé en 1736 par Euler. Il est aujourd’hui résolu, mais les habitants de Koenigsberg (aujourd’hui Kaliningrad) ne savaient pas comment faire. La ville de Koenigsberg comprenait 2 îles et 7 ponts, suivant le plan ci-contre. Les habitants souhaitaient faire une promenade passant une et une seule fois sur chaque pont. Y sont-ils arrivés ?
L’IREM d’Aix-Marseille publie Graphes pour la Terminale ES. Outre les éléments essentiels de la théorie des graphes, ce document comporte de nombreux exercices (avec les corrigés) et problèmes, comme celui des ponts de Koenigsberg, ainsi que des pistes pour aller plus loin, concernant la modélisation.
Un azulejo créé par Eduardo Nery
Les azulejos s’assemblent dans toutes les orientations possibles en respectant une continuité de couleurs et de motifs. Regardez le film dont le lien se trouve dans Etude de quelques AZULEJOS. Des azulejos plastifiés sont d’abord présentés aux élèves comme « un trésor » caché dans une enveloppe, ils vont ensuite être étudiés tout au long de l’année. Au rythme des séances, les élèves découvrent différents azulejos et un grand nombre de questions.