De la tablette aux dominos, la recette c'est la récurrence !
La récurrence, c'est comme le chocolat : quand on commence un carré, on finit la tablette ; nul ne résiste au goût du reviens-y 1. Et l'on peut (souvent) ne pas avoir attendu le programme de Terminale 2, qui pose toute cette belle théorie, pour en faire l'expérience.
Après les bons mots, voyons comment traiter, justement grâce au principe d'induction, un petit problème anodin mais réputé avoir séché d'éminents mathématiciens 3.
Voici la scène. Vous avez devant vous une plaquette de chocolat tout ce qu'il y a de plus banale : rectangulaire, au format mettons $m\times n$. Vous souhaitez la diviser pour en récupérer tous les petits carreaux. À chaque étape du processus,
- vous pouvez prendre un morceau et le rompre en suivant soit une ligne soit une colonne. Auquel cas, toute la ligne ou toute la colonne y passe ;
- vous ne pouvez pas superposer ou juxtaposer deux morceaux pour gagner du temps : vous cassez tout à la main, sans support et sans scie.
La figure suivante illustre sur un cas particulier ce que pourraient être les deux premières étapes du mode opératoire.
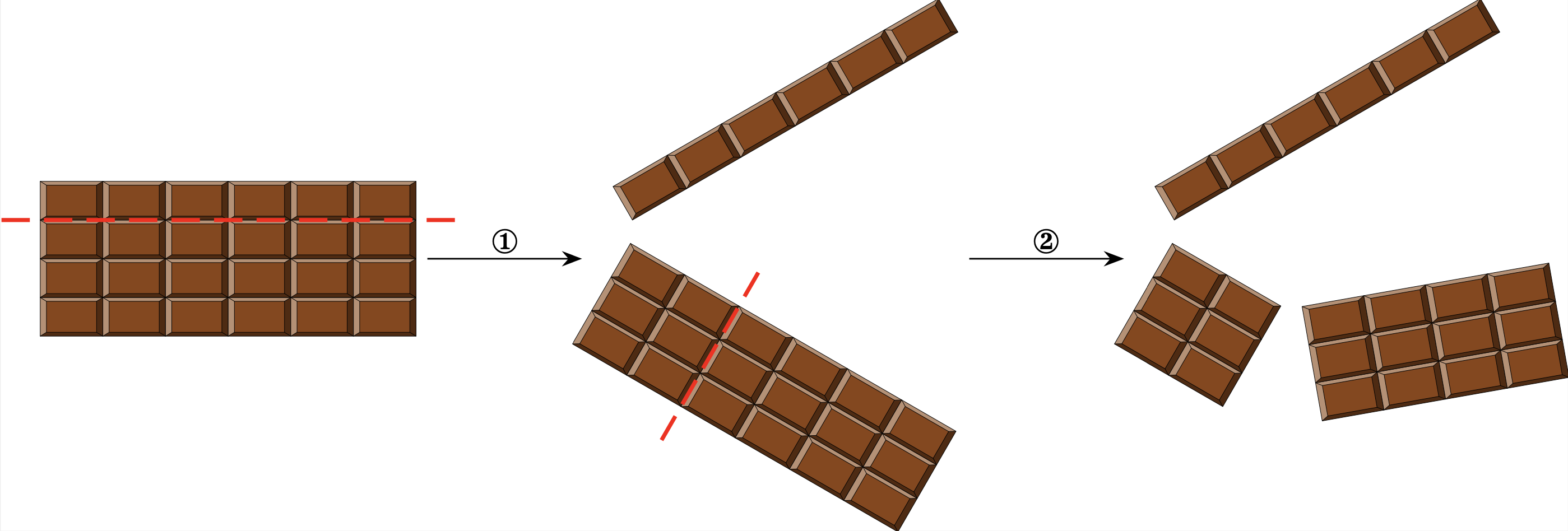
Deux étapes de la réduction d'une tablette de chocolat.
Question
Prouvez que le nombre d'étapes à suivre pour séparer tous les carrés les uns des autres reste invariablement le même, quelle que soit la manière de s'y prendre, dans le respect des règles édictées ci-dessus cependant.
Il est sous-entendu que les dimensions $m$ et $n$ sont ici fixées.
La solution repose sur une récurrence tenant dans le choix judicieux de son hypothèse au rang $k$, ainsi que dans une bonne compréhension de sa terminaison. Nous énonçons comme proposition $\mathcal{P}(k)$ : « À l'issue de la $k$-ième étape, on dispose de $k+1$ morceaux ».
- $\mathcal{P}(1)$ est manifestement vraie. Une première coupe longitudinale ou verticale de la tablette la réduit en deux morceaux, eux-mêmes à nouveau rectangulaires ;
- Tant que la tablette n'est pas entièrement réduite, l'implication logique $\left(\mathcal{P}(k) \Rightarrow \mathcal{P}(k+1)\right)$ est vraie. L'action consiste à choisir un morceau qui peut encore se subdiviser et à le fragmenter ;
- Le procédé s'achève à l'étape $(m\times n) - 1$ comme le présageait l'hypothèse de récurrence. Il produit en effet $m \times n$ morceaux qui ne peuvent qu'être des carrés individuels sauf à tomber dans l'absurde.
En informatique, la variable calculée en soustrayant du rang le nombre de morceaux de chocolat s'appellerait un invariant de boucle. En mathématiques, le chocolat est toujours un bon adjuvant 4. Bref, l'esprit léger, il ne vous reste plus qu'à enfiler le tablier de cuisine, à préparer le dessert puis à le consommer sans modération !







