Une découverte due aux travaux menés, au milieu du XIX^e siècle, de façon presque simultanée et pourtant indépendante, par le mathématicien allemand Moritz Stern, à qui l’on doit une étude poussée des fractions continues1, et Achille Brocot, horloger français et « mathématicien à ses heures »2, qui s’intéressait aux approximations fractionnaires pour mener des calculs d’engrenages, donne des éléments de réponse à cette question. De façon plus précise, nous allons voir comment, à partir des fractions « spéciales » \(0/1\) et \(1/0\), et de cette opération « particulière », il est possible de construire un arbre binaire contenant tous les rationnels positifs écrits sous forme irréductible. Sur le plan pédagogique, si la construction de cet arbre est aisée à mettre en œuvre, l’étude de ses propriétés fait appel, parfois de manière originale, à des résultats classiques sur les suites, d’arithmétique ou de calcul matriciel. Elle permet également la mise en œuvre d’algorithmes, dont nous proposons ici une implémentation sous python. Il y a donc matière à intéresser les élèves ou les étudiants ayant un penchant pour les mathématiques ou l’informatique, du secondaire ou de l’enseignement supérieur, à partir des curiosités de cet arbre.

Notations et conventions

La plupart des notations ou conventions adoptées dans cet article sont tout à fait usuelles ; celles qui pourraient ne pas l'être, ou proprement liées à notre étude, sont mentionnées au fil du texte. La seule sur laquelle nous souhaitons nous attarder est la suivante : comme indiqué en introduction, nous allons « bousculer » les habitudes en nous autorisant à manipuler des fractions de la forme $a/0$, où $a \in \mathbb{N}^*$. Nous assimilerons ces fractions à l'élément $+\infty$, supposé strictement supérieur à tout nombre réel.

Au départ : médiante et fractions adjacentes

Pour faire « pousser » notre arbre de Stern-Brocot et apprécier comme il se doit ses propriétés, il convient de présenter deux concepts qui occuperont une place prépondérante dans ce qui suit. Le premier d’entre eux est celui de fractions adjacentes. Étant donnés $a, b, c, d \in \mathbb{N}$, nous dirons que $a/b$ est adjacente à $c/d$ si la quantité : \[\left|\!\begin{array}{cc}b & d \\ a & c\end{array}\!\right| \ = \ bc - ad\] est égale à $1$ (c’est un déterminant, mais il n’est pas nécessaire de savoir de quoi il s’agit pour comprendre ce qui suit). On notera que cette relation d’adjacence n’est pas symétrique. Malgré tout, lorsqu’aucune ambigüité ne sera possible, il nous arrivera simplement de dire que $a/b$ et $c/d$ sont adjacentes. Nous pouvons d’ores et déjà effectuer les quelques observations suivantes :

Le deuxième concept au cœur de notre étude est celui de médiante de deux fractions : étant donnés $a, b, c, d \in \mathbb{N}$, on définit la médiante de $a/b$ et $c/d$ en posant : \[\frac{a}{b} \oplus \frac{c}{d} \ = \ \frac{a + c}{b + d}\text{.}\] Le résultat suivant montre que la notion d’adjacence est en quelque sorte préservée par l’opération médiante :

Silence, ça pousse !

Pour faciliter son élaboration comme son étude, nous allons construire l'arbre de Stern-Brocot en deux temps. On commence par construire la suite des suites (finies) de Stern-Brocot :

• On pose $S_0 = (0/1, \: 1/0)$.
• Pour tout $n \in \mathbb{N}$, ayant construit $S_n = (a_1/b_1, \: a_2/b_2, \: \dots \: , \: a_k/b_k)$, on construit la suite $S_{n+1}$ à partir de $S_n$ en insérant, entre toutes les fractions consécutives de la suite $S_n$, la médiante de ces deux fractions :
  \[S_{n+1} = \left(\frac{a_1}{b_1}, \: \frac{a_1}{b_1} \oplus \frac{a_2}{b_2}, \: \frac{a_2}{b_2}, \: \dots \:, \: \frac{a_{k-1}}{b_{k-1}} \oplus \frac{a_k}{b_k}, \: \frac{a_k}{b_k}\right)\text{.}\]

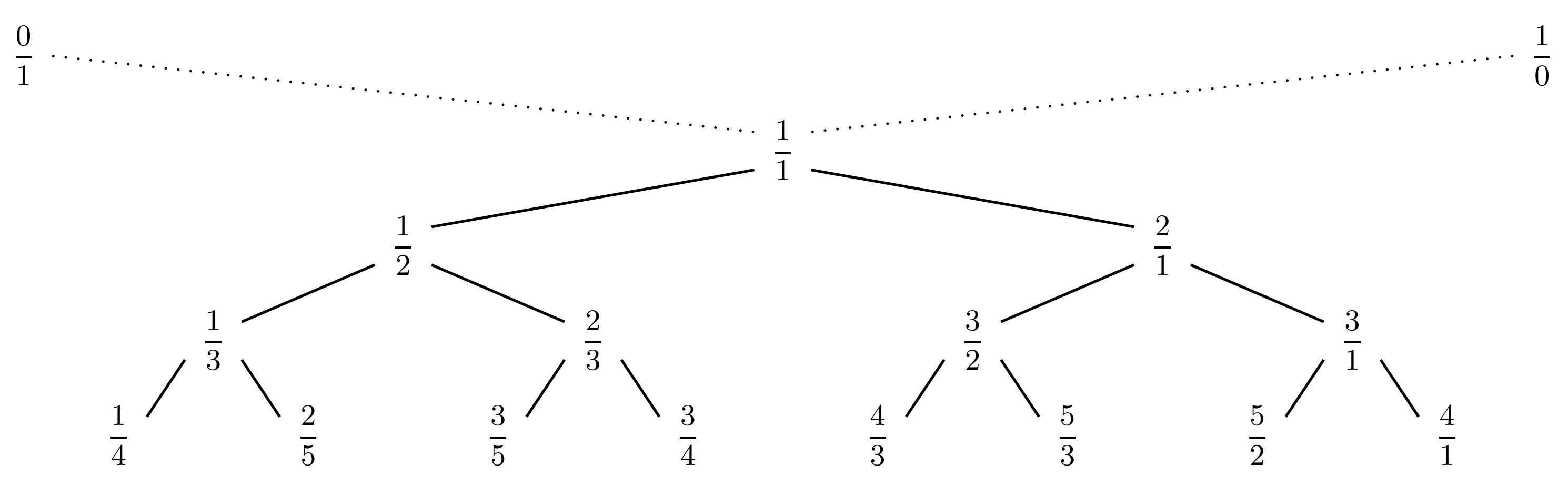
Pour la compréhension, explicitons les cinq premières suites finies de Stern-Brocot :
\begin{align*}
S_0 & = \left(\frac{0}{1}, \: \frac{1}{0}\right)\text{,} \\
S_1 & = \left(\frac{0}{1}, \: \frac{1}{1}, \: \frac{1}{0}\right)\text{,} \\
S_2 & = \left(\frac{0}{1}, \: \frac{1}{2}, \: \frac{1}{1}, \: \frac{2}{1}, \: \frac{1}{0}\right)\text{,} \\
S_3 & = \left(\frac{0}{1}, \: \frac{1}{3}, \: \frac{1}{2}, \: \frac{2}{3}, \: \frac{1}{1}, \: \frac{3}{2}, \: \frac{2}{1}, \: \frac{3}{1}, \: \frac{1}{0}\right)\text{,} \\
S_4 & = \left(\frac{0}{1}, \: \frac{1}{4}, \: \frac{1}{3}, \: \frac{2}{5}, \: \frac{1}{2}, \: \frac{3}{5}, \: \frac{2}{3}, \: \frac{3}{4}, \: \frac{1}{1}, \: \frac{4}{3}, \: \frac{3}{2}, \: \frac{5}{3}, \: \frac{2}{1}, \: \frac{5}{2}, \: \frac{3}{1}, \: \frac{4}{1}, \: \frac{1}{0}\right)\text{.}
\end{align*}

La proposition suivante précise la structure de ces suites (finies) de Stern-Brocot :

Comme on le constate, pour tout $n \in \mathbb{N}$, $S_n$ est une sous-suite de $S_{n+1}$. Les suites de Stern-Brocot ainsi construites contiennent donc une information redondante, qu'il serait judicieux de supprimer. La figure suivante présente les suites $S_0$ à $S_4$ dans lesquelles l'information redondante apparait en rouge.

Pour ce faire, il suffit de poser $B_0 = S_0 = (0/1, \: 1/0)$ puis, pour tout $n \in \mathbb{N}$, de ne stocker dans $B_{n+1}$ que les médiantes construites à partir de la suite $S_n$. Les cinq premiers termes de cette suite $(B_n)_{n \in \mathbb{N}}$ sont donc :
\[
B_0 \: = \: \left(\frac{0}{1}, \: \frac{1}{0}\right)\text{,} \ \ B_1 \: = \: \left(\frac{1}{1}\right)\text{,} \ \ B_2 \: = \: \left(\frac{1}{2}, \: \frac{2}{1}\right)\text{,} \ \ B_3 \: = \: \left(\frac{1}{3}, \: \frac{2}{3}, \: \frac{3}{2}, \: \frac{3}{1}\right)\text{,} \\ B_4 \: = \: \left(\frac{1}{4}, \: \frac{2}{5}, \: \frac{3}{5}, \: \frac{3}{4}, \: \frac{4}{3}, \: \frac{5}{3}, \: \frac{5}{2}, \: \frac{4}{1}\right)\text{.}
\]
On peut ainsi construire un arbre binaire dont la racine est l'unique fraction de $B_1$, à savoir la fraction $1/1$ (la médiante des fractions $0/1$ et $1/0$ de $B_0$), et dont les étages inférieurs sont construits successivement à partir des fractions apparaissant dans les suites $B_2$, $B_3$, $B_4$, etc.

Sur les branches de l'arbre : tous les rationnels

Une caractéristique remarquable de cet arbre est qu'à partir des seules fractions $0/1$ et $1/0$ et de l'opération médiante, on parvient à (re)construire tous les nombres rationnels, bien entendu strictement positifs (on ne le précisera plus systématiquement), écrits sous forme irréductible. Pour prouver cela, on va raisonner par l'absurde et supposer disposer d'un rationnel $r = p/q$ strictement positif n'apparaissant dans aucune des suites $S_n$ de Stern-Brocot. Montrons qu'il est alors possible de construire une suite $(I_n)_{n \in \mathbb{N}}$ d'intervalles ouverts où, pour tout $n \in \mathbb{N}$, les extrémités de $I_n$ sont consécutives dans la suite $S_n$, et donc adjacentes d'après le point 2 de la proposition 3.

• Au départ, on a naturellement $r \in \ ]0, +\infty[ \ = \ ]0/1, \: 1/0[$ : on pose $I_0 = \ ]0/1, \: 1/0[$.
• Soit $n \in \mathbb{N}$ et supposons avoir construit un intervalle ouvert $I_n = \ ]\alpha, \beta[$ contenant $r$, et dont les extrémités sont consécutives, et donc adjacentes, dans $S_n$. Soit $m = \alpha \oplus \beta$. Comme $r$ n'apparait pas dans $S_{n+1}$, on a $r < m$ ou $r > m$ : on pose $I_{n+1} = \ ]\alpha, m[$ dans le premier cas et $I_{n+1} = \ ]m, \beta[$ dans le second. Le fait que les extrémités de l'intervalle $I_{n+1}$ soient adjacentes est une conséquence de la proposition 2.

Les suites $S_n$ de Stern-Brocot sont construites de telle sorte que lorsque $n$ augmente, il en va de même pour les numérateurs et dénominateurs des extrémités des intervalles $I_n$. Or, le fait que les extrémités d'un tel intervalle soient adjacentes va permettre de « contrôler »  leurs numérateurs et dénominateurs par ceux de tout rationnel compris dans cet intervalle. C'est ce que précise le lemme suivant :

Nous disposons à présent de tous les éléments nous permettant d'aboutir à une contradiction ; il ne nous reste plus qu'à formaliser tout cela. Étant donnés $a, b, c, d \in \mathbb{N}$ et $I = \ ]a/b, \: c/d[$, posons :
\[\mu(I) = a + b + c + d \ \in \mathbb{N}\text{.}\]
D'après le lemme 4, nous avons tout d'abord $\mu(I_n) \leq p + q$ pour tout $n \in \mathbb{N}$. Ensuite, si $n \in \mathbb{N}$ et $I_n = \ ]a/b, \: c/d[$, $a/b$ est (par construction) adjacente à $c/d$. En particulier, on a donc $b$ et $c$ non nuls d'après le point 1 de la proposition 1. Or, soit $I_{n+1} = \: ]a/b, \: a/b \oplus c/d[$, auquel cas $\mu(I_{n+1}) = 2a + 2b + c + d > a + b + c + d = \mu(I_n)$, soit $I_{n+1} = \: ]a/b \oplus c/d, \: c/d[$, auquel cas $\mu(I_{n+1}) = a + b + 2c + 2d > a + b + c + d = \mu(I_n)$. Mais, dans un cas comme dans l'autre, nous avons bien $\mu(I_{n+1}) > \mu(I_n)$.
Par conséquent, $\big(\mu(I_n)\big)_{n \in \mathbb{N}}$ est une suite d'entiers strictement croissante et majorée par $p + q$ : c'est impossible. Ceci montre que notre hypothèse initiale, à savoir que $r$ n'apparait dans aucune des suites $S_n$ de Stern-Brocot, était fausse. Ainsi, tout rationnel strictement positif apparait dans l'une des suites de Stern-Brocot, écrit sous forme irréductible d'après le point 2 de la proposition 3. Et comme les suites $B_n$, construites à partir des suites $S_n$ de Stern-Brocot et ayant donné naissance à l'arbre du même nom, contiennent au plus une fois chaque rationnel, nous avons finalement démontré le résultat suivant :

Chemin d'un rationnel dans l'arbre de Stern-Brocot

Nous venons de voir que tout nombre rationnel strictement positif apparait une et une seule fois dans l'arbre de Stern-Brocot. Ainsi, à tout rationnel $r \in \mathbb{Q}_+^*$, il est possible d'associer un unique chemin $\mathrm{ch}(r)$ dans l'arbre de Stern-Brocot, à savoir une suite finie de symboles $\mathrm{D}$ (pour droite) et $\mathrm{G}$ (pour gauche) indiquant quelle(s) direction(s) emprunter depuis la racine $1/1$ de cet arbre pour atteindre le nœud où le rationnel $r$ apparait. Inversement, à tout chemin $\gamma$, c'est-à-dire à toute suite finie constituée à partir des symboles $\mathrm{D}$ et $\mathrm{G}$, il est possible d'associer un unique rationnel strictement positif, noté $\mathrm{rat}(\gamma)$ : celui qui possède $\gamma$ pour chemin dans l'arbre de Stern-Brocot. Notons $\{\mathrm{D}, \mathrm{G}\}^*$ l'ensemble des chemins (suites finies de symboles $\mathrm{D}$ et $\mathrm{G}$), qui correspond théoriquement au monoïde engendré par $\mathrm{D}$ et $\mathrm{G}$ pour la concaténation (remarque culturelle, sans importance dans la suite de cette section). Les applications :
\[\mathrm{ch} \ : \ \mathbb{Q}_+^* \rightarrow \{\mathrm{D}, \mathrm{G}\}^*, \ r \mapsto \mathrm{ch}(r) \ \ \ \ \ \ \text{et} \ \ \ \ \ \ \mathrm{rat} \ : \ \{\mathrm{D}, \mathrm{G}\}^* \rightarrow \mathbb{Q}_+^*, \ \gamma \mapsto \mathrm{rat}(\gamma)\]
ainsi construites sont donc deux bijections, réciproques l'une de l'autre. Cependant, ce simple constat ne nous sera d'aucune utilité dans la suite de cette section ; il n'est donc pas nécessaire de savoir ce qu'est une bijection pour comprendre ce que nous y exposons.
Pour mieux appréhender l'effet de ces applications $\mathrm{ch}$ et $\mathrm{rat}$, donnons l'exemple suivant.

Dans ce qui suit, étant donnés deux chemins $\gamma = (s_1, s_2, \dots, s_k)$ et $\gamma' = (s_1', s_2', \dots, s_l')$, nous désignerons par :

•  $\gamma \cdot \gamma'$ la concaténation des chemins $\gamma$ et $\gamma'$, définie par $\gamma \cdot \gamma' = (s_1, s_2, \dots, s_k, s_1', s_2', \dots, s_l')$. En particulier, désignant par $\epsilon$ un symbole parmi $\mathrm{G}$ ou $\mathrm{D}$, on pose $\epsilon \cdot \gamma = (\epsilon) \cdot \gamma$ et $\gamma \cdot \epsilon = \gamma \cdot (\epsilon)$.
•  $\gamma^{-1}$ l'opposé du chemin $\gamma$, obtenu en remplaçant, dans $\gamma$, tous les symboles $\mathrm{G}$ par $\mathrm{D}$, et vice-versa.

Comme nous pouvons l'observer sur les exemples précédents ou, plus généralement, sur les premiers étages de l'arbre de Stern-Brocot (voir la figure 2), il semblerait que les chemins menant à un rationnel $r = p/q$ strictement positif et à son inverse $r^{-1} = q/p$ soient opposés. Ce fait, vrai en toute généralité, est une simple conséquence du point 3 de la proposition 3 et du principe de construction de l'arbre de Stern-Brocot à partir des suites $B_n$. Nous pouvons le formaliser de la façon suivante :

Nous allons maintenant nous intéresser à la problématique suivante : étant donné un rationnel $r \in \mathbb{Q}_+^*$, situer $r$ dans l'arbre de Stern-Brocot, autrement dit déterminer le chemin $\mathrm{ch}(r)$ conduisant à $r$ depuis la racine $1/1$ de l'arbre. À partir de la démonstration du théorème 5 menée dans la section 3, nous allons même pouvoir faire plus (et mieux) : déterminer $\mathrm{ch}(r)$ et expliciter les parents de $r$, c'est-à-dire les fractions $a/b$ et $c/d$ dont $r$ est la médiante.

Au départ, nous savons que $r$ appartient à l'intervalle $I_0 = \ ]0, +\infty[ \ = \ ]0/1, \: 1/0[$. On pose alors $\mathrm{ch}(r) = ( \ )$, puis on regarde la médiante $0/1 \oplus 1/0 = 1/1$ des extrémités de $I_0$.

• Si $r = 1/1$, on s'arrête (déjà !) : on a trouvé $r$ et ses parents, à savoir $0/1$ et $1/0$.
• Si $r < 1/1$, alors $r \in \ ]0/1, \: 1/1[$. On doit donc partir à gauche dans l'arbre, et on fait $\mathrm{ch}(r) \leftarrow \mathrm{ch}(r) \cdot \mathrm{G}$.
• Si $r > 1/1$, alors $r \in \ ]1/1, \: 1/0[$. On doit donc partir à droite dans l'arbre, et on fait $\mathrm{ch}(r) \leftarrow \mathrm{ch}(r) \cdot \mathrm{D}$.

Supposons avoir déterminé, pour un entier $n \in \mathbb{N}$ donné, un intervalle $I_n = \ ]\alpha, \beta[$ contenant $r$ aux extrémités consécutives dans la suite $S_n$ de Stern-Brocot. On regarde la médiante $m = \alpha \oplus \beta$ des extrémités de $I_n$.

• Si $r = m$, on s'arrête : on a trouvé $r$ et ses parents, à savoir $\alpha$ et $\beta$.
• Si $r < m$, alors $r \in \ ]\alpha, m[$. On doit donc partir à gauche dans l'arbre, et on fait $\mathrm{ch}(r) \leftarrow \mathrm{ch}(r) \cdot \mathrm{G}$.
• Si $r > m$, alors $r \in \ ]m, \beta[$. On doit donc partir à droite dans l'arbre, et on fait $\mathrm{ch}(r) \leftarrow \mathrm{ch}(r) \cdot \mathrm{D}$.

Or, comme nous l'avons vu, ce processus de recherche de $r$ par dichotomie s'arrête après un nombre fini d'étapes.  Nous sommes donc certains d'atteindre le rationnel $r$ et ses parents en effectuant ces encadrements successifs. Sous Python, cet algorithme de recherche peut être codé comme suit :

def RechercheSB1(p, q, affiche) :
# EN ENTREE :
# - numerateur "p" et denominateur "q" du rationnel r = p/q recherche.
# - "affiche" : booleen permettant un affichage en sortie s'il est affecte a True.
# EN SORTIE :
# - liste "chemin" de symboles G et D indiquant comment trouver r dans l'arbre,
# - numerateurs "a" et "c" et denominateurs "b" et "d" des parents a/b et c/d de r.

    # Au depart, r est compris entre a/b = 0/1 et c/d = 1/0...
    [a, b, c, d] = [0, 1, 1, 0]
    # ... et le chemin menant a r est vide.
    chemin = []

    # Tant que p/q n'est pas egal a la mediante de a/b et c/d :
    while (p/q != (a+c)/(b+d)) :

        # Si p/q est plus petit que la mediante :
        if (p/q < (a+c)/(b+d)) :
            # On part a gauche dans l'arbre.
            chemin.append("G")
            # On remplace c/d par la mediante de a/b et c/d.
            c = a+c
            d = b+d

        # Si p/q est plus grand que la mediante de a/b et c/d :
        else :
            # On part a droite dans l'arbre.
            chemin.append("D")
            # On remplace c/d par la mediante de a/b et c/d.
            a = a+c
            b = b+d

    # Pour un affichage :
    if affiche :
        print("Le chemin menant a ",p,"/",q," est : ",chemin)
        print("Les parents de ",p,"/",q," sont : ",a,"/",b," et ",c,"/",d)

    return chemin, a, b, c, d

Tant pour nous assurer de la validité de notre code que celle des propos tenus précédemment, on commence par tester notre algorithme sur les situations de l’exemple précédent. Nous effectuons ensuite des tests plus « poussés », en recherchant les chemins de rationnels moins « élémentaires » :

>> RechercheSB1(1, 2, True)
Le chemin menant a  1 / 2  est :  ['G']
Les parents de  1 / 2  sont :  0 / 1  et  1 / 1

>> RechercheSB1(2, 1, True)
Le chemin menant a  2 / 1  est :  ['D']
Les parents de  2 / 1  sont :  1 / 1  et  1 / 0

>> RechercheSB1(3, 2, True)
Le chemin menant a  3 / 2  est :  ['D', 'G']
Les parents de  3 / 2  sont :  1 / 1  et  2 / 1

>> RechercheSB1(2, 3, True)
Le chemin menant a  2 / 3  est :  ['G', 'D']
Les parents de  2 / 3  sont :  1 / 2  et  1 / 1

>> RechercheSB1(2, 5, True)
Le chemin menant a  2 / 5  est :  ['G', 'G', 'D']
Les parents de  2 / 5  sont :  1 / 3  et  1 / 2

>> RechercheSB1(5, 2, True)
Le chemin menant a  5 / 2  est :  ['D', 'D', 'G']
Les parents de  5 / 2  sont :  2 / 1  et  3 / 1

>> RechercheSB1(17, 39, True)
Le chemin menant a  17 / 39  est :  ['G', 'G', 'D', 'D', 'D', 'G', 'G', 'D']
Les parents de  17 / 39  sont :  10 / 23  et  7 / 16

>> RechercheSB1(11, 50, True)
Le chemin menant a  11 / 50  est :  ['G', 'G', 'G', 'G', 'D', 'G', 'D', 'D', 'D', 'D']
Les parents de  11 / 50  sont :  9 / 41  et  2 / 9

>> RechercheSB1(73, 26, True)
Le chemin menant a  73 / 26  est :  ['D', 'D', 'G', 'D', 'D', 'D', 'D', 'G', 'G', 'G', 'G']
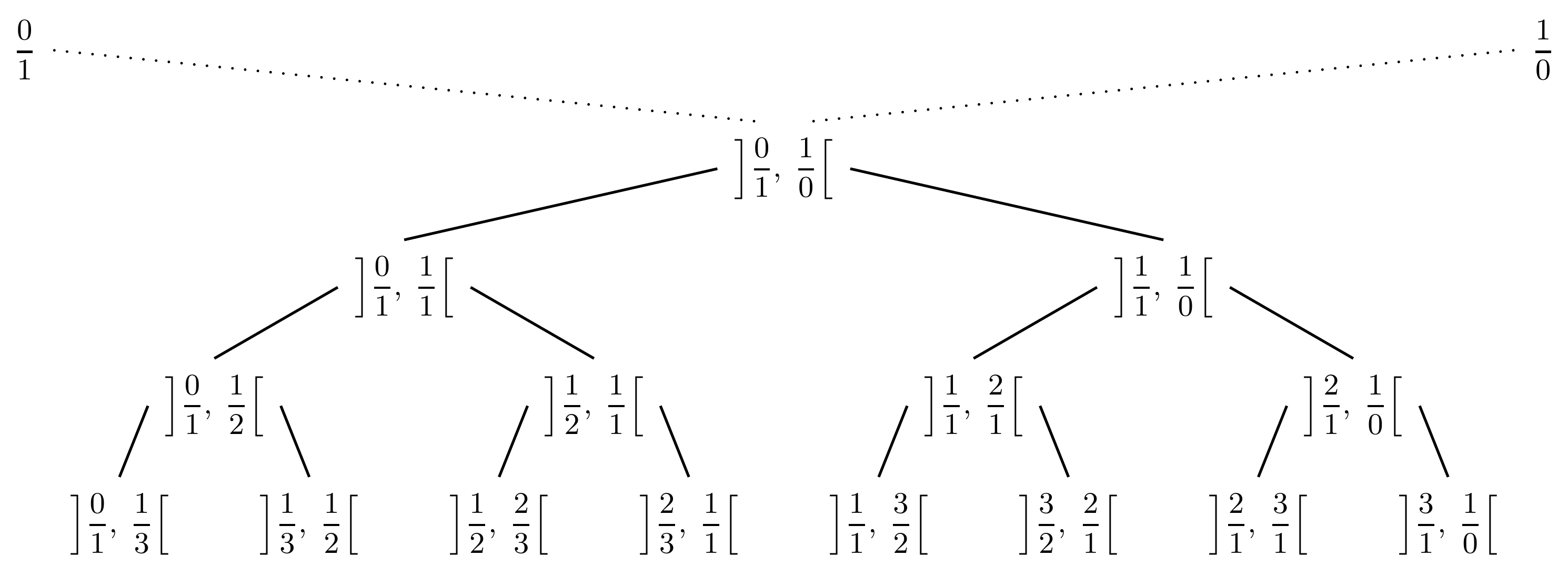
Les parents de  73 / 26  sont :  14 / 5  et  59 / 21

En résumé, l'algorithme précédent nous permet de retrouver le chemin conduisant à n'importe quel rationnel strictement positif dans l'arbre de Stern-Brocot. Plus encore, il nous permet également d'associer à tout $r \in \mathbb{Q}_+^*$ un intervalle $I_r = \ ]a/b, \: c/d[$ contenant $r$, dont les extrémités sont consécutives, et donc adjacentes, dans l'une des suites $S_n$ de Stern-Brocot, et tel que $r = a/b \oplus c/d$.

De cette façon, il est possible de constituer un arbre à intervalles en remplaçant chaque rationnel $r$ apparaissant dans l'arbre de Stern-Brocot par l'intervalle $I_r$ susmentionné. La figure suivante, à mettre en lien avec la figure 2, présente les premiers étages de cet arbre à intervalles.

Approche matricielle

À tout rationnel strictement positif $x/y$ écrit sous forme irréductible, on associe le vecteur :
\[\left(\!\begin{array}{c}y \\ x\end{array}\!\right)\text{,}\]
dont le rationnel $x/y$ représente la pente. De cette façon, à un intervalle $]a/b, \: c/d[$ de l'arbre à intervalles, on convient d'associer la matrice :
\[\left(\!\begin{array}{cc}b & d \\ a & c\end{array}\!\right)\text{.}\]
Notons d'ores et déjà que :

• Les extrémités d'un tel intervalle étant adjacentes, la matrice qui lui correspond est de déterminant $1$, autrement dit un élément de $\mathrm{SL}_2(\mathbb{N})$.
• Si $r$ est le rationnel associé à l'intervalle $]a/b, \: c/d[$ dans l'arbre de Stern-Brocot, autrement dit si $r = a/b \oplus c/d$, alors le vecteur associé à $r$ est :

\begin{align}\left(\!\begin{array}{c}b + d \\ a + c\end{array}\!\right) = \left(\!\begin{array}{cc}b & d \\ a & c\end{array}\!\right)\left(\!\begin{array}{c}1 \\ 1\end{array}\!\right)\text{.}\end{align}

Désignons à présent par $r$ un rationnel strictement positif et par $I_r = \ ]a/b, \: c/d[$ l'intervalle associé à $r$ dans l'arbre à intervalles, de sorte que $r = a/b \oplus c/d$. Partant du rationnel $r$ dans l'arbre de Stern-Brocot ou, de façon équivalente, de l'intervalle $I_r$ dans l'arbre à intervalles :

• Si l'on se dirige à droite, autrement dit si l'on effectue la concaténation $\mathrm{ch}(r) \leftarrow \mathrm{ch}(r) \cdot \mathrm{D}$, on tombe alors sur l'intervalle $]r, c/d[ \ = \ ]a/b \oplus c/d, \: c/d[$, qui est associé à la matrice :

\begin{align}\left(\!\begin{array}{cc}b + d & d \\ a + c & c\end{array}\!\right) = \left(\!\begin{array}{cc}b & d \\ a & c\end{array}\!\right)\left(\!\begin{array}{cc}1 & 0 \\ 1 & 1\end{array}\!\right)\text{.}\end{align}
 

• Si l'on se dirige à gauche, autrement dit si l'on effectue la concaténation $\mathrm{ch}(r) \leftarrow \mathrm{ch}(r) \cdot \mathrm{G}$, on tombe alors sur l'intervalle $]a/b, r[ \ = \ ]a/b, \: a/b \oplus c/d[$, qui est associé à la matrice :

\begin{align}\left(\!\begin{array}{cc}b & b + d \\ a & a + c\end{array}\!\right) = \left(\!\begin{array}{cc}b & d \\ a & c\end{array}\!\right)\left(\!\begin{array}{cc}1 & 1 \\ 0 & 1\end{array}\!\right)\text{.}\end{align}
 

Posons :
\begin{align*}
D = \left(\!\begin{array}{cc}1 & 0 \\ 1 & 1\end{array}\!\right) \ \ \ \ \ \ \text{et} \ \ \ \ \ \ G = \left(\!\begin{array}{cc}1 & 1 \\ 0 & 1\end{array}\!\right)\text{.}
\end{align*}
Soit $\gamma = \mathrm{ch}(r)$ le chemin menant à $r$ dans l'arbre de Stern-Brocot ou, de façon équivalente, à l'intervalle $I_r$ dans l'arbre à intervalles. Notons $\mathrm{mat}(\gamma)$ la matrice obtenue en remplaçant, dans $\gamma$, tous les symboles $\mathrm{D}$ par la matrice $D$ et tous les symboles $\mathrm{G}$ par la matrice $G$, puis en faisant le produit de ces matrices. Formellement, si $\gamma = (s_1, s_2, \dots, s_k)$, on a donc :
\[\mathrm{mat}(\gamma) = \textstyle{\prod\limits_{i = 1}^k S_i} \ \ \ \ \ \ \text{où} \ \ \ \ \ \ \left\{\begin{array}{ccc}S_i = D & \text{si} & s_i = \mathrm{D}\text{,} \\ S_i = G & \text{si} & s_i = \mathrm{G}\text{.}\end{array}\right.\]
En observant les premiers étages de l'arbre de Stern-Brocot et de l'arbre à intervalles (figures 2 et 3), on semble conjecturer le résultat suivant :

Finalement, sur le même modèle que l'arbre à intervalles, il est donc possible de constituer un arbre à matrices en remplaçant chaque rationnel $r$ de l'arbre de Stern-Brocot par la matrice $\mathrm{mat}\!\big(\!\mathrm{ch}(r)\big)$. Les premiers étages de ce nouvel arbre sont présentés dans la figure 4.

Euclide et les fractions continues

Laissons un instant notre arbre de Stern-Brocot de côté, et livrons-nous à quelques rappels d'arithmétique. Nous allons à présent nous intéresser aux fractions continues (positives), c'est-à-dire à des quotients de la forme :
\[q_0 + \cfrac{1}{\:q_1 + \cfrac{1}{\begin{array}{@{}c@{}c}\ddots & \\[-0.3cm] & \: q_{n-1} + \cfrac{1}{q_n}\end{array}}\:} \ \text{,}\]
où $n \in \mathbb{N}$, $q_0 \in \mathbb{N}$ et $q_1, \dots, q_n \in \mathbb{N}^*$. Pour alléger les notations, il est d'usage de noter $[q_0, q_1, \dots, q_n]$ ce quotient, qui correspond évidemment à un nombre rationnel positif.
Une conséquence de l'algorithme d'Euclide est que tout nombre rationnel positif peut s'écrire sous forme d'une fraction continue. Rappelons le principe de cet algorithme. Étant donnés $a, b \in \mathbb{N}$ avec $b \neq 0$, on construit deux suites $(q_k)_{k \in \mathbb{N}}$ et $(r_k)_{k \in \mathbb{N}}$ de la manière suivante :

• On pose tout d'abord $r_{-1} = a$ et $r_0 = b$.
• Pour tout $k \in \mathbb{N}$, lorsque $r_{k} \neq 0$, on considère l'unique couple $(q_{k}, r_{k+1})$ vérifiant les relations :

\[r_{k-1} = r_{k}q_{k} + r_{k+1} \ \ \ \ \ \ \text{et} \ \ \ \ \ \ 0 \ \leq\ r_{k+1} \ < \ r_{k}\text{.}\]
En d'autres termes, $q_{k}$ et $r_{k+1}$ correspondent respectivement au quotient et au reste de la division euclidienne de $r_{k-1}$ par $r_{k}$. Et lorsque $r_{k} = 0$, on pose $q_{k} = r_{k+1} = 0$.

La suite d'entiers naturels $(r_k)_{k \in \mathbb{N}}$  ainsi construite étant strictement décroissante jusqu'à un certain rang, elle finit par s'annuler définitivement. Notons $n$ le plus petit entier naturel $k$ vérifiant $r_{k+1} = 0$. Pour tout $k \in \{0, \dots n\}$, on a alors :
\[\frac{r_{k-1}}{r_k} = \frac{r_kq_k + r_{k+1}}{r_k} = q_k + \frac{r_{k+1}}{r_k}\text{,}\]
et donc, lorsque $r_{k+1} > 0$ :
\[\frac{r_{k-1}}{r_k} = q_k + \frac{1}{r_{k}/r_{k+1}}\text{.}\]
De proche en proche, on constate ainsi que :
\begin{align*}
\frac{a}{b} = \frac{r_{-1}}{r_0} = q_0 + \frac{1}{r_0/r_1} = q_0 + \cfrac{1}{\: q_1 + \cfrac{1}{r_1/r_2}\:} = \cdots = q_0 + \cfrac{1}{\: q_1 + \cfrac{1}{\begin{array}{@{}c@{}c}\ddots & \\[-0.3cm] & \: q_{n-1} + \cfrac{1}{q_n}\end{array}}\:} = [q_0, q_1, \dots, q_n]\text{.}
\end{align*}
Et comme, pour tout $k \in \{0, \dots, n\}$, on a $r_{k-1} = r_kq_k + r_{k+1}$ avec $0 \leq r_{k+1} < r_k$, on constate que $q_k \geq 1$. Ayant en outre, lorsque $k = n$, $r_{n-1} = r_nq_n + r_{n+1} = r_nq_n$, on remarque que $q_n \geq 2$. En définitive, nous avons établi le résultat suivant :

Pour terminer cette section, nous pouvons présenter la fonction Python suivante, qui permet d'expliciter la liste des quotients successifs apparaissant dans l'algorithme d'Euclide appliqué à deux entiers $a$ et $b$ donnés, et qui détermine donc la décomposition du rationnel $a/b$ sous forme d'une fraction continue :

def QuotientsEuclide(a, b) :
# EN ENTREE :
# - entiers "a" et "b" auquel on applique l'algorithme d'Euclide.
# EN SORTIE :
# - liste "L" des quotients apparaissant dans cet algorithme d'Euclide.

    L = []
    [q, r] = [0, 0]

        while (b != 0) :
        # On effectue la division euclidienne de a par b : a = bq + r :
        r = a%b
        # Ainsi, q = (a-r)/b :
        L.append((a-r)/b)
        # On poursuit l'algorithme avec b et r :
        a = b
        b = r

    return L

Euclide et Stern-Brocot : même combat ?

Cette digression arithmétique étant faite, revenons sur les branches de notre arbre. Désignons par $s$ un symbole parmi $\mathrm{D}$ et $\mathrm{G}$, et posons $s^0 = ( \ )$ puis, pour tout $q \in \mathbb{N}$, $s^{q+1} = s \cdot s^q$. Pour ainsi dire, pour tout $q \in \mathbb{N}$, on a donc :
\[\mathrm{D}^q = \underbrace{(\mathrm{D}, \mathrm{D}, \dots, \mathrm{D})}_{q \ \text{composantes}} \ \ \ \ \ \ \text{et} \ \ \ \ \ \ \mathrm{G}^q = \underbrace{(\mathrm{G}, \mathrm{G}, \dots, \mathrm{G})}_{q \ \text{composantes}}\text{.}\]
Soient à présent $\gamma$ un chemin, $r = \mathrm{rat}(\gamma)$ le rationnel ayant pour chemin dans l'arbre de Stern-Brocot, et
\[M = \left(\!\begin{array}{cc}b & d \\ a & c\end{array}\!\right)\]
la matrice associée à $r$ dans l'arbre à matrices, de sorte que :
\[r = \frac{a}{b} \oplus \frac{c}{d} = \frac{a + c}{b + d}\text{.}\]
D'après le théorème 8, ayant :
\[DM = \left(\!\begin{array}{cc}b & d \\ b + a & d + c\end{array}\!\right)\text{,}\]
on constate que le rationnel ayant pour chemin $\mathrm{D} \cdot \gamma$ dans l'arbre de Stern-Brocot est :
\[\frac{b + a}{b} \oplus \frac{d + c}{d} = \frac{a + b + c + d}{b + d} = 1 + \frac{a + c}{b + d} = 1 + r\text{.}\]
De la même façon, ayant :
\[GM = \left(\!\begin{array}{cc}b + a & d + c \\ a & c\end{array}\!\right)\text{,}\]
on constate que le rationnel ayant $\mathrm{G} \cdot \gamma$ pour chemin dans l'arbre de Stern-Brocot est :
\[\frac{a}{b + a} \oplus \frac{c}{d + c} = \frac{a + c}{a + b + c + d} = \frac{1}{\: \displaystyle \frac{a + b + c + d}{a + c} \: } = \frac{1}{1 + \displaystyle \frac{b + d}{a + c}} = \frac{1}{1 + 1/r} = \frac{r}{1 + r}\text{.}\]
Définissons alors :
\[\mathrm{d} \ : \ \rho \mapsto 1 + \rho \ \ \ \ \ \ \text{et} \ \ \ \ \ \ \mathrm{g} \ : \ \rho \mapsto \frac{\rho}{1 + \rho} = \frac{1}{1 + 1/\rho}\text{.}\]
Pour tous $q \in \mathbb{N}$ et $\rho \in \mathbb{Q}$, ayant clairement :
\[\mathrm{d}^{(q)}(\rho) = q + \rho \ \ \ \ \ \ \text{et} \ \ \ \ \ \ \mathrm{g}^{(q)}(\rho) = \frac{\rho}{1 + q\rho} = \frac{1}{q + 1/\rho}\text{,}\]
on déduit de ce qui précède le résultat suivant :

Soit $\gamma$ un chemin ; $\gamma$ étant, par définition, une suite finie dans laquelle les symboles $\mathrm{D}$ et $\mathrm{G}$ se succèdent, il est toujours possible de déterminer d'uniques entiers $n \in \mathbb{N}$, $q_0 \in \mathbb{N}$ et $q_1, \dots, q_n \in \mathbb{N}^*$ tels que :

• $\gamma = \mathrm{D}^{q_0} \cdot \mathrm{G}^{q_1} \cdot \mathrm{D}^{q_2} \cdot \: \cdots \: \cdot \mathrm{G}^{q_{n-1}} \cdot \mathrm{D}^{q_n}$ lorsque $n$ est pair,
• $\gamma = \mathrm{D}^{q_0} \cdot \mathrm{G}^{q_1} \cdot \mathrm{D}^{q_2} \cdot \: \cdots \: \cdot \mathrm{D}^{q_{n-1}} \cdot \mathrm{G}^{q_n}$ lorsque $n$ est impair.

Supposons $n$ pair. D'après la proposition 12, de proche en proche, on obtient alors :
\begin{align*}
\mathrm{rat}(\gamma) & = \mathrm{rat}(\mathrm{D}^{q_0} \cdot \mathrm{G}^{q_1} \cdot \mathrm{D}^{q_2} \cdot \: \cdots \: \cdot \mathrm{G}^{q_{n-1}} \cdot \mathrm{D}^{q_n}) \\
& = q_0 + \mathrm{rat}(\mathrm{G}^{q_1} \cdot \mathrm{D}^{q_2} \cdot \: \cdots \: \cdot \mathrm{G}^{q_{n-1}} \cdot \mathrm{D}^{q_n}) \\
& = q_0 + \frac{1}{q_1 + \mathrm{rat}(\mathrm{D}^{q_2} \cdot \: \cdots \: \cdot \mathrm{G}^{q_{n-1}} \cdot \mathrm{D}^{q_n})} \\
& \enspace \vdots \\
& = q_0 + \cfrac{1}{\: q_1 + \cfrac{1}{\begin{array}{@{}c@{}c}\ddots & \\[-0.3cm] & \: q_{n-1} + \cfrac{1}{\mathrm{rat}(\mathrm{D}^{q_n})}\end{array}}\:} \\
& = q_0 + \cfrac{1}{\: q_1 + \cfrac{1}{\begin{array}{@{}c@{}c}\ddots & \\[-0.3cm] & \: q_{n-1} + \cfrac{1}{q_n + \mathrm{rat}( \ )}\end{array}}\:}\ \text{,}
\end{align*}
De la même manière, lorsque $n$ est impair, on obtient :
\[\mathrm{rat}(\gamma) = q_0 + \cfrac{1}{\: q_1 + \cfrac{1}{\begin{array}{@{}c@{}c}\ddots & \\[-0.1cm] & \: q_{n-1} + \mathrm{rat}(\mathrm{D}^{q_n})\end{array}}\:} = q_0 + \cfrac{1}{\: q_1 + \cfrac{1}{\begin{array}{@{}c@{}c}\ddots & \\[-0.3cm] & \: q_{n-1} + \cfrac{1}{q_n + \mathrm{rat}( \ )}\end{array}}\:}\]
Et puisque $\mathrm{rat}( \ ) = 1/1$, on a donc obtenu, en toute généralité :
\[\mathrm{rat}(\gamma) = q_0 + \cfrac{1}{\: q_1 + \cfrac{1}{\begin{array}{@{}c@{}c}\ddots & \\[-0.3cm] & \: q_{n-1} + \cfrac{1}{q_n + 1}\end{array}}\:} = [q_0, q_1, \dots, q_{n-1}, q_n, 1] = [q_0, q_1, \dots, q_{n-1}, q_n + 1]\text{.}\]
Tout nombre rationnel apparaissant une et une seule fois dans l'arbre de Stern-Brocot, en vertu du théorème 11, nous avons donc établi le résultat suivant :

Ce théorème nous fournit une deuxième façon de retrouver le chemin d'un rationnel dans l'arbre de Stern-Brocot. Sous Python, il peut être implémenté comme suit :

def RechercheSB2(p, q, affiche) :
# EN ENTREE :
# - numerateur "p" et denominateur "q" du rationnel r = p/q recherche.
# - "affiche" : booleen permettant un affichage en sortie s'il est affecte a True.
# EN SORTIE :
# - liste "chemin" de symboles G et D indiquant comment trouver r dans l'arbre.

    # Au depart, le chemin menant a p/q est vide.
    chemin = []

    # On recupere la liste des quotients dans l'algorithme d'Euclide applique a p et q.
    L = QuotientsEuclide(p,q)
    L = list(map(int, L)) # Pour convertir les elements de L en int.
    n = len(L) # Taille de L.

    # Si L = (q0, q1, ... , qn), alors :
    # - chemin = D^q0 G^q1 D^q2 ... D^q_{n-1} G^{qn - 1} lorsque n est pair,
    # - chemin = D^q0 G^q1 D^q2 ... G^q_{n-1} D^{qn - 1} lorsque n est impair.
    L[n-1] = L[n-1] - 1

    for i in range(n) :
        # Si i est pair, alors on va qi=L[i] fois a droite :
        if (i%2 == 0) :
            for j in range(L[i]) :
                chemin.append('D')
        # Si i est impair, alors on va qi=L[i] fois a gauche :
        else :
            for j in range(L[i]) :
                chemin.append('G')

    if affiche :
        print(L)

    return chemin

Pour s'assurer de la validité de ce deuxième algorithme de recherche dans l'arbre de Stern-Brocot, on peut créer la fonction Python suivante qui prend en entrée deux entiers $p$ et $q$ et teste si les chemins menant au rationnel $p/q$ retournés par les fonctions RechercheSB1 et RechercheSB2 sont identiques :

def TestRecherches(p, q, affiche) :
# EN ENTREE :
# - numerateur "p" et denominateur "q" du rationnel r = p/q recherche.
# - "affiche" : booleen permettant un affichage en sortie s'il est affecte a True.
# EN SORTIE :
# - booleen "verif" qui teste si RechercheSB1 et RechercheSB2 renvoient le meme chemin vers p/q.

    chemin1 = RechercheSB2(p, q, False)
    chemin2, a, b, c, d = RechercheSB1(p, q, False)
    verif = (chemin1 == chemin2) # on teste si chemin1 = chemin2.

    if affiche :
        print(verif)

    return verif

Pour se rassurer, on peut effectuer les quelques sorties suivantes :

>> TestRecherches(1, 1, True)
True

>> TestRecherches(1, 2, True)
True

>> TestRecherches(2, 5, True)
True

>> TestRecherches(8, 3, True)
True

>> TestRecherches(17, 39, True)
True

>> TestRecherches(115, 47, True)
True

Conclusion

Si la construction de l'arbre de Stern-Brocot est très simple à mettre en œuvre, elle conduit à des résultats tout à fait remarquables d'un point de vue mathématique (et algorithmique). Mentionnons notamment le fait que l'on trouve ainsi, dans l'arbre, une et une seule fois tous les rationnels strictement positifs écrits sous forme irréductible, ou que le chemin menant à un tel rationnel (dans l'arbre) permet de retrouver sa décomposition sous forme de fraction continue, et peut donc être retrouvé par simple application de l'algorithme d'Euclide.
Sur le plan pédagogique, la construction de l'arbre de Stern-Brocot et l'étude de ses propriétés peut ainsi donner lieu à de jolis développements, notamment sous forme de projet ou de devoir à la maison. Si, dès le collège, certains résultats présentés dans cet article peuvent être assez facilement conjecturés, les démonstrations sont à réserver aux lycéens ou aux étudiants de premières années post-bac, notamment en C.P.G.E. ou dans les cursus universitaires de mathématiques ou d'informatique. Soulignons en particulier que la partie algorithmique pourra aussi bien permettre d'intéresser des étudiants en informatique aux mathématiques ou, à l'inverse, d'initier les mathématiciens à l'algorithmique et à la programmation.

Pour aller plus loin

Mentionnons d'abord quelques références qui pourraient être utiles au lecteur: un exercice proposant de retrouver quelques propriétés de l'arbre,1 des résultats sur les fractions continues2 et une vidéo présentant le sujet.3

Pour terminer, nous présentons ici quelques résultats ou ouvertures possibles autour de l'étude de l'arbre de Stern-Brocot menée dans cet article :

Le théorème 5 stipule que tout rationnel strictement positif apparait une et une seule fois dans l'arbre. Par conséquent, l'application $\mathrm{ch} : \mathbb{Q}_+^* \rightarrow \{\mathrm{D}, \mathrm{G}\}^*$, qui associe à chaque rationnel strictement positif son chemin (suite finie de symboles $\mathrm{D}$ et $\mathrm{G}$) dans l'arbre de Stern-Brocot, est bijective.

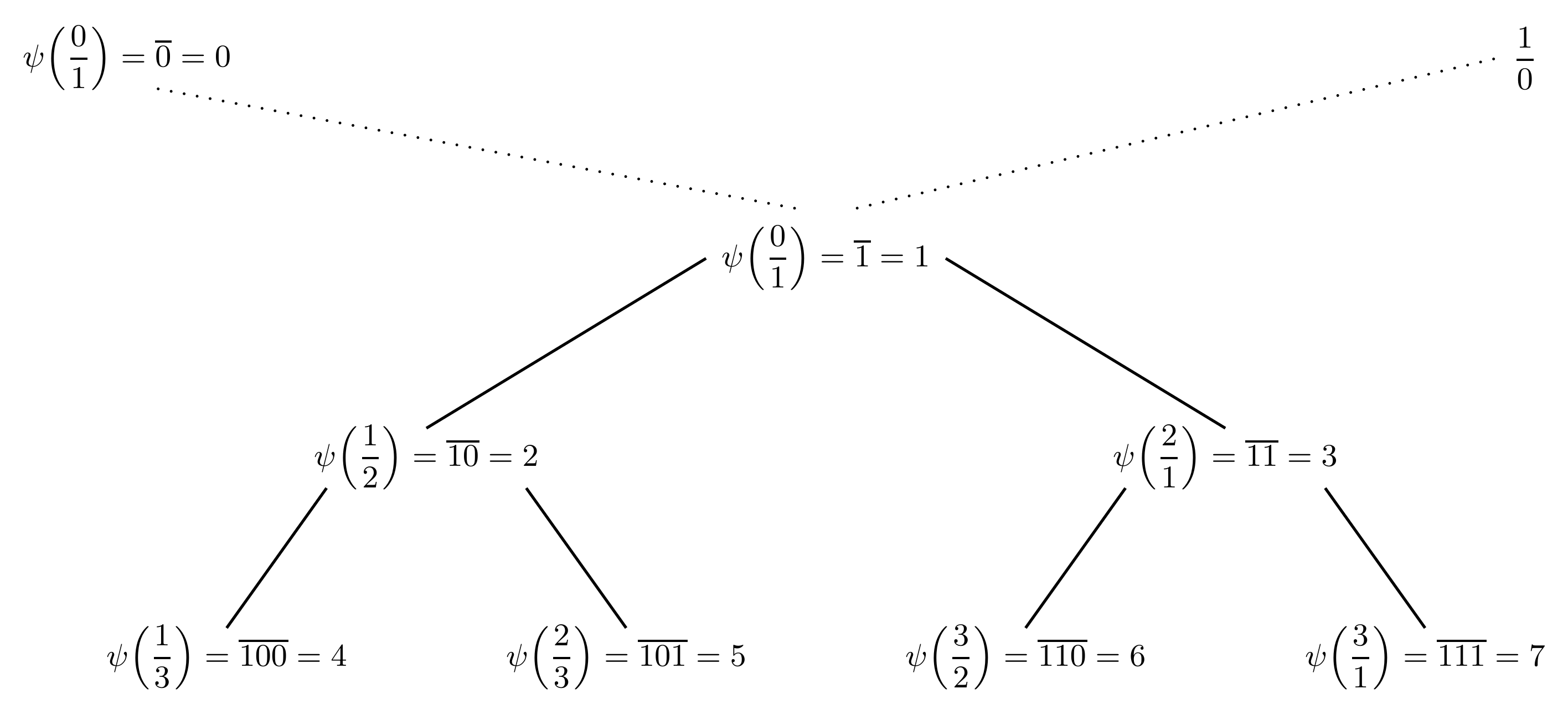
Pour rappel, tout entier naturel $n$ non nul admet une unique écriture en base $2$ dont le premier chiffre (celui de gauche) est égal à $1$, puisqu'il existe d'uniques $k \in \mathbb{N}^*$ et $c_0, c_1 \dots , c_{k-1} \in \{0,1\}$ tels que :
\[n = c_02^0 + c_12^1 + \dots + c_{k-1}2^{k-1} + 1\!\cdot\!2^k\text{.}\]
S'il en est ainsi, nous noterons $\overline{1c_{k-1} \cdots c_1 c_0}$ l'écriture en base $2$ de $n$.  Compte tenu de ces deux remarques, à partir de la correspondance $\mathrm{G} \leftrightarrow 0$ et $\mathrm{D} \leftrightarrow 1$, on parvient à construire une bijection $\psi : \mathbb{Q}_+ \rightarrow \mathbb{N}$ en posant :
\[\psi\!\left(\frac{0}{1}\right) = 0\text{,}\]
puis, pour tout $r \in \mathbb{Q}_+^*$ tel que $\mathrm{ch}(r) = (s_1, \dots, s_k)$ :
\[\psi(r) = \overline{1c_1\dots c_k} \ \ \ \ \ \ \text{où} \ \ \ \ \ \ \left\{\begin{array}{ccc}c_i = 1 & \text{si} & s_i = \mathrm{D}\text{,} \\ c_i = 0 & \text{si} & s_i = \mathrm{G}\text{.}\end{array}\right.\]
On en déduit ainsi le caractère dénombrable de $\mathbb{Q}_+$.

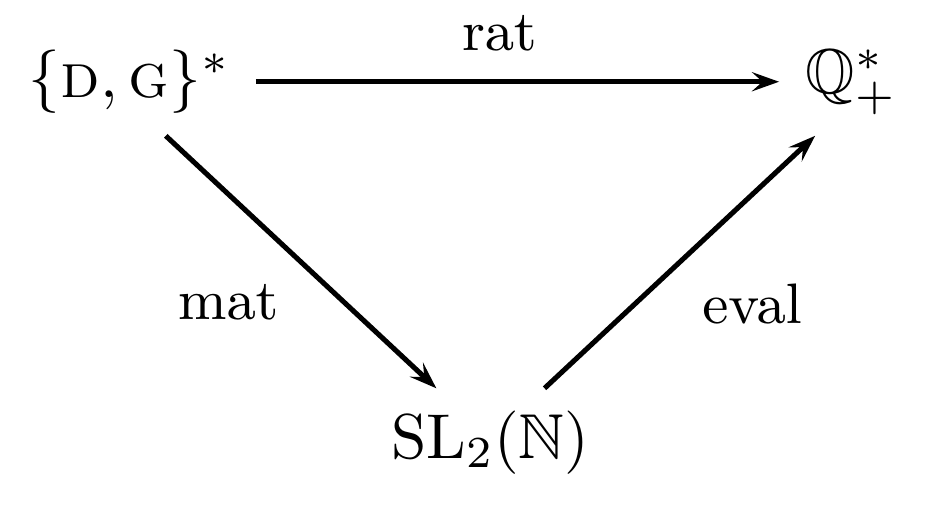
Soit $\mathrm{eval}: \mathrm{SL}_2(\mathbb{N}) \rightarrow \mathbb{Q}_+^*$ l'application qui, à une matrice $M$, associe le rationnel ayant pour vecteur $M\binom{1}{1}$, à partir de la correspondance $x/y \leftrightarrow \binom{y}{x}$ effectuée à la section 5. Une conséquence du théorème 8 est que $\mathrm{rat} = \mathrm{eval} \circ \mathrm{mat}$, autrement dit que le diagramme suivant est commutatif :

Or, comme nous l'avons vu, l'application $\mathrm{rat} : \{\mathrm{D}, \mathrm{G}\}^* \rightarrow \mathbb{Q}_+^*$ est bijective, de bijection réciproque l'application $\mathrm{ch} : \mathbb{Q}_+^* \rightarrow \{\mathrm{D}, \mathrm{G}\}^*$. En outre, l'application $\mathrm{eval} : \mathrm{SL}_2(\mathbb{N}) \rightarrow \mathbb{Q}_+^*$ est la bijection réciproque de l'application qui, à tout rationnel $r$, associe la matrice de $\mathrm{SL}_2(\mathbb{N})$ placée sur le nœud de $r$ dans l'arbre à matrices. D'un point de vue algébrique, on en déduit que les monoïdes $\{\mathrm{D}, \mathrm{G}\}^*$ (muni de la concaténation) et $\mathrm{SL}_2(\mathbb{N})$ (muni du produit matriciel) sont isomorphes. En particulier, $\mathrm{SL}_2(\mathbb{N})$ est donc engendré par les matrices :
\begin{align*}
D = \left(\!\begin{array}{cc}1 & 0 \\ 1 & 1\end{array}\!\right) \ \ \ \ \ \ \text{et} \ \ \ \ \ \ G = \left(\!\begin{array}{cc}1 & 1 \\ 0 & 1\end{array}\!\right)\text{.}
\end{align*}
Autrement dit : $\mathrm{SL}_2(\mathbb{N}) = \{D, G\}^*$.

Si l'on s'autorise à manipuler des suites infinies de symboles $\mathrm{D}$ et $\mathrm{G}$, l'arbre de Stern-Brocot permet d'atteindre tous les nombres réels strictement positifs. Pour ce faire, si $x$ est le réel strictement positif que l'on souhaite atteindre, il suffit d'utiliser le même algorithme que celui présenté à la section 4, permettant de retrouver un rationnel $r$ donné dans l'arbre, en y remplacer $r$ par $x$. Bien entendu, une conséquence du théorème 5 est que l'algorithme s'arrête après un nombre fini d'étapes si et seulement si $x$ est rationnel.
Par exemple, le chemin menant au nombre d'or $\phi$ est donné par $(\mathrm{D}, \mathrm{G}, \mathrm{D}, \mathrm{G}, \mathrm{D}, \mathrm{G}, \mathrm{D}, \mathrm{G}, \dots )$. Ceci ne surprendra pas les lectrices et lecteurs avertis, puisque si l'on observe les rationnels apparaissant sur les branches de ce chemin, on retrouve les termes $F_{n+1}/F_n$, où $(F_n)_{n\in \mathbb{N}}$ désigne la suite de Fibonacci, qui convergent vers $\phi$.
D'une façon générale,  à partir de cet algorithme, sur chaque étage $n$ de l'arbre, on dispose d'une approximation rationnelle $p_n/q_n$ du réel $x$ que l'on souhaite atteindre. On peut montrer qu'il s'agit là de la meilleure approximation rationnelle de $x$ en le sens suivant : pour tous $p, q \in \mathbb{N}$ vérifiant soit $0 < q < q_n$, soit $q = q_n$ et $p \neq p_n$, on a $|p - xq| > |p_n - xq_n|$, dont on déduit bien entendu $|p/q - x| > |p_n/q_n - x|$.
Enfin, une autre conséquence de cette approche de $\mathbb{R}_+^*$ par « chemins infinis » est que l'on parvient à construire une bijection entre $\{\mathrm{D}, \mathrm{G}\}^\mathbb{N}$ et $\mathbb{R}_+^*$, dont on déduit le caractère non dénombrable de $\mathbb{R}_+^*$ (et donc de $\mathbb{R}$).

Remerciements

Je tiens à remercier Guillaume Malod et Dominique Baroux d'avoir relu cet article et des conseils dont ils ont pu me faire part à son sujet. Je souhaiterais également remercier Claude Quitté qui, lorsque j'étais encore étudiant, m'a fait découvrir les curiosités de cet arbre à travers un projet d'informatique pour les mathématiques, que j'ai mené en collaboration avec Alexis Puygrenier ; dix ans après, celles-ci continuent de m'intéresser...