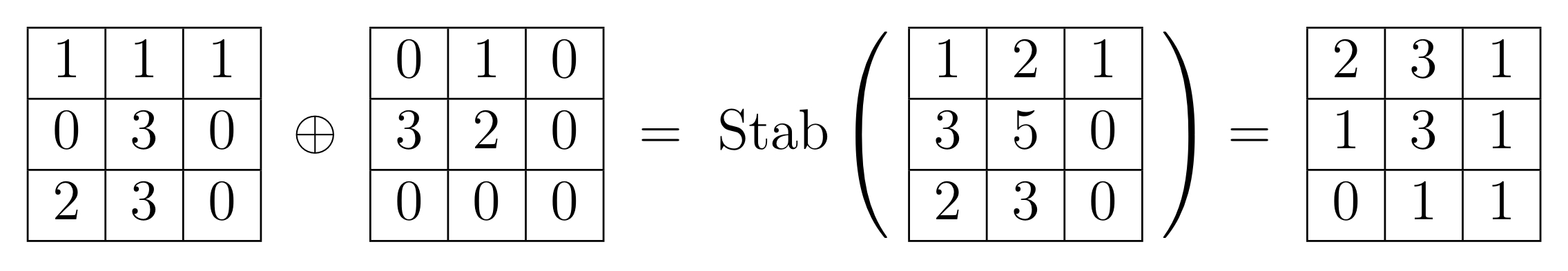Vous trouvez zéro sans intérêt ? C'est parce que vous n'avez pas encore fait la rencontre de ses cousins colorés issus des tas de sable !
Notion d’élément neutre
Bien qu’il ait fallu attendre longtemps pour avoir l’idée du zéro, aujourd’hui il nous paraît quelque peu banal. $$0+0=0.$$ $0~+$ n’importe quel nombre, ça donne ce même nombre. $0$ multiplié par n’importe quoi fait toujours $0$… Zéro ne nous fait pas bouger avec sa forme arrondie toute sage. Cependant, zéro joue un rôle spécial dans les nombres, tout comme son (grand) camarade $1$. En effet, un nombre auquel on ajoute $0$ reste inchangé. En termes plus mathématiques, pour tout nombre réel $x$, $$0+x=x+0 =x.$$ Du côté de la multiplication, tout nombre multiplié par $1$ reste inchangé, i.e, pour tout nombre réel $x$, $$1.x=x.1 =x.$$ Ces deux nombres ont une propriété intéressante par rapport respectivement à l’addition et la multiplication. On appelle cette propriété « être élément neutre » relativement à une opération. Zéro est ainsi l’élément neutre pour l’addition des nombres réels (et complexes), tandis que un est l’élément neutre pour la multiplication des nombres réels (ou complexes).
On peut cependant imaginer des opérations sur d’autres objets mathématiques que des nombres.
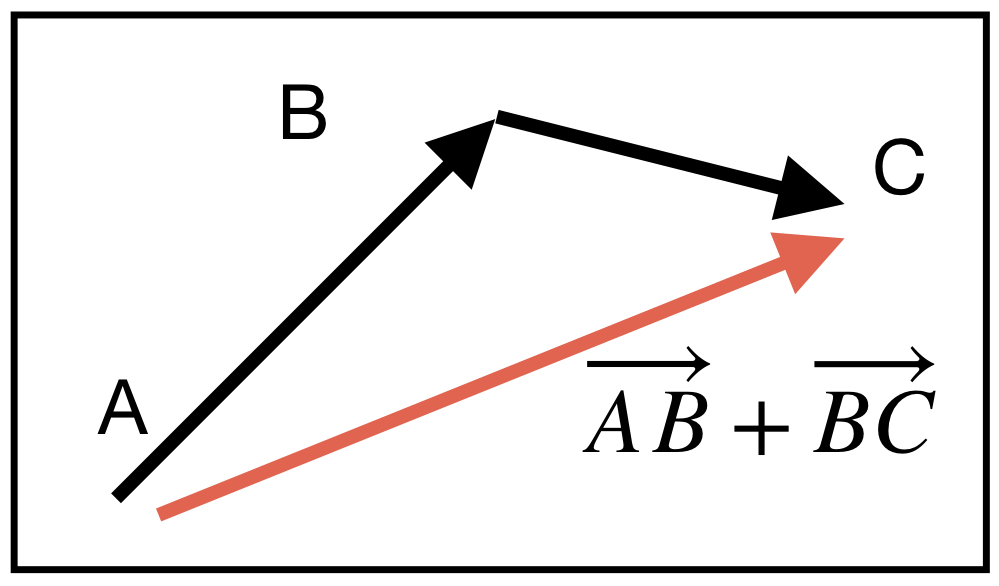
On peut ainsi additionner des vecteurs du plan $\vec{AB} + \vec{CD}$ comme sur la figure 1. Cela revient à additionner les coordonnées des vecteurs. Ici encore l’addition sur l’ensemble des vecteurs du plan admet un élément neutre qui est le vecteur nul de coordonnées $(0,0)$, qui n’est guère plus palpitant que $0$.
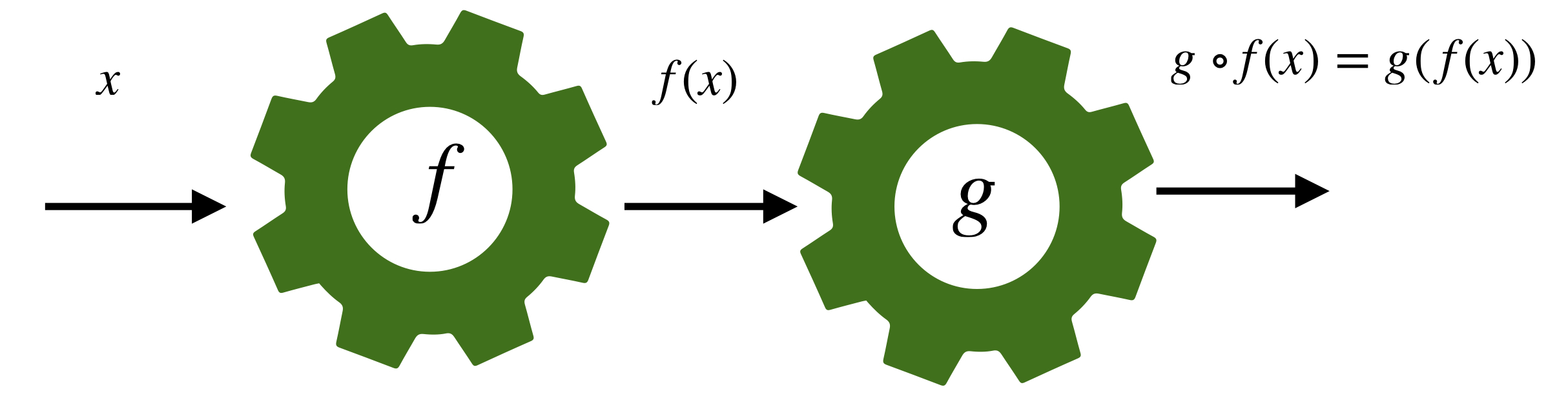
On peut aussi définir l’opération suivante sur l’ensemble des fonctions de $\mathbb{R}$ dans $\mathbb{R}$, appelée composition. Soient $f$ et $g$ deux fonctions de $\mathbb{R}$ dans $\mathbb{R}$. On définit un nouvelle fonction, qui est la composée de $f$ par $g$, notée $g\circ f$ (lire g rond f) qui est la fonction valant en tout nombre $x$ : $$ (g\circ f)(x) = g(f(x)).$$ C’est-à-dire que pour un nombre $x$, on calcule d’abord son image par $f$, $f(x)$, puis l’image par $g$ de $f(x)$.
Cette opération admet elle aussi un élément neutre : la fonction identité, qui est la fonction qui à tout nombre $x$ associe $x$. Là encore, l’identité est une fonction bien basique, comme vous pouvez le voir sur sa courbe représentative figure 3.
Le modèle du tas de sable
Venons-en au but de cet article, qui est de vous présenter un élément neutre, un « zéro » beaucoup moins monotone que les précédents. Pour cela, il me faut commencer par vous expliquer le modèle du tas de sable.
Prenons une grille carrée. On distingue sur la grille, les cases « frontières » (se trouvant sur le bord de la grille) des cases intérieures. Sur chaque case intérieure, nous plaçons un certain nombre de grains de sable. Cette grille sur laquelle sont disposés des grains de sable est appelée tas de sable. Comme vous l’avez sans doute déjà observé à la plage, si l'on met trop de sable en un même endroit, le tas s’écroule et les grains s’éparpillent tout autour, c’est pourquoi nous distinguons les tas de sable stables (qui ne s’écroulent pas et que l'on nommera par la suite TSS) des tas instables. Un tas de sable est dit stable, si sur chaque case le nombre de grains n’est pas trop grand, en l’occurrence ici inférieur ou égal à 3.
Les cases frontières quant à elles fonctionnent comme des puits pour recueillir le sable issu des écroulements. Lorsqu’un grain de sable tombe dans le puit, c’est comme s’il disparaissait du système.
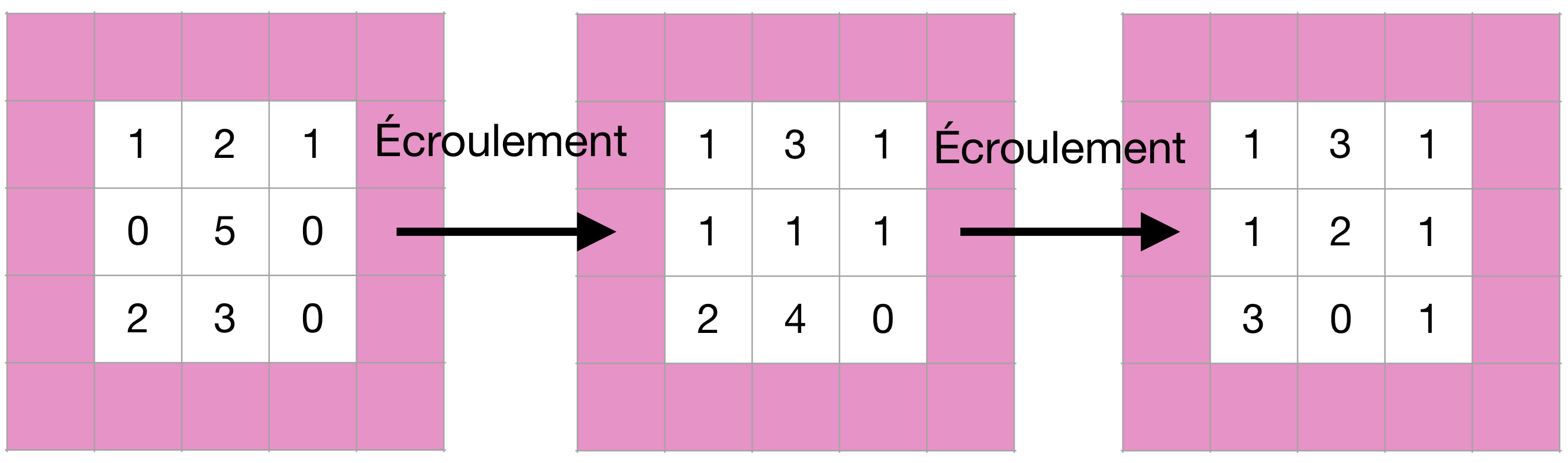
Mais comment un tas de sable s’écroule-t-il dans notre modèle? Si une case a au moins 4 grains de sable, on dit que le sommet s’écroule, en donnant un grain de sable à chacun de ses 4 voisins. Si le sommet est voisin d’un sommet frontière, alors il donne un grain de sable (voire deux s’il est sur un coin) à un puits. Ces grains de sable disparaissent alors du système. On appelle stabilisation du tas de sable la série d’écroulements des sommets instables. On peut montrer que tout tas de sable admet une stabilisation unique, c’est-à-dire que l’ordre des écroulements n’influence pas le résultat final.
La case centrale a 5 grains de sable, le tas de sable est donc instable. On écroule le sommet, le tas de sable est toujours instable. On écroule à nouveau le sommet et on obtient un tas de sable stable (on note que lors de cette dernière opération, l’un des grains de la case de coordonnées (3,2) est tombé dans le puits).
Notre objectif est de trouver un élément neutre « original ». Pour cela, nous avons besoin de définir une opération sur les tas de sable stables. Il est naturel d’additionner deux tas de sable (stables ou instables) en sommant case par case le nombre de grains. Pour définir une opération sur les tas de sable stables seulement, on considère la stabilisation de l’addition des tas de sable. On note cette addition $\oplus$. Cette addition est commutative et associative. Ces mots barbares signifient intuitivement que l’ordre dans lequel on effectue plusieurs additions n’a pas d’influence sur le résultat.
On voit encore une fois que le tas de sable sur lequel il n’y a justement aucun grain de sable est élément neutre pour cette addition. Nous l’appelons le tas nul (noté $0_{\mathrm{TSS}}$). Cependant, il manque une propriété très intéressante mathématiquement à cette addition. Revenons pour cela aux nombres réels. Pour tout nombre $x$, on peut trouver un $y$ (qui est égal à $-x$) tel que $y+x=0$. Peut-on faire la même chose avec les tas de sable stables? La réponse est non! Pour tout TSS $t$ (non nul), il est en fait impossible de trouver un TSS $t'$ tel que $t \oplus t' = 0_{\mathrm{TSS}} $. C’est dommage car à peu de choses près l’ensemble des tas de sable stables muni de cette addition est un groupe, une structure mathématique fondamentale (mais néanmoins très courante, puisqu'on la côtoie dès que l'on sait additionner des entiers relatifs... cliquer ici pour en voir une définition).
Mais pas de problème! On peut en fait montrer qu’il existe un sous-ensemble $G$ des tas de sable stable qui pour l’addition est un groupe, c’est-à-dire que, en particulier,
- si l'on a deux tas de sable stable de cet ensemble $G$, leur somme est encore dans $G$ ;
- on peut trouver un élément neutre (un « zéro ») dans $G$, c’est-à-dire un tas de sable spécial noté $\Delta$ tel que
- la somme de tout TSS $t$ de $G$ et de $\Delta$ est encore égale à $t$ : $$t \oplus \Delta = t,$$
- et pour tout tas de sable $t$ de $G$ il existe un tas de sable $ t'$ de $G$ tel que la somme de $t$ et $t'$ nous donne l'élément neutre : $$t \oplus t'=\Delta.$$
L’ensemble des TSS récurrents G, c’est-à-dire des TSS obtenus en stabilisant un tas de sable ayant un nombre minimal de grains sur chaque case, forme un tel groupe.
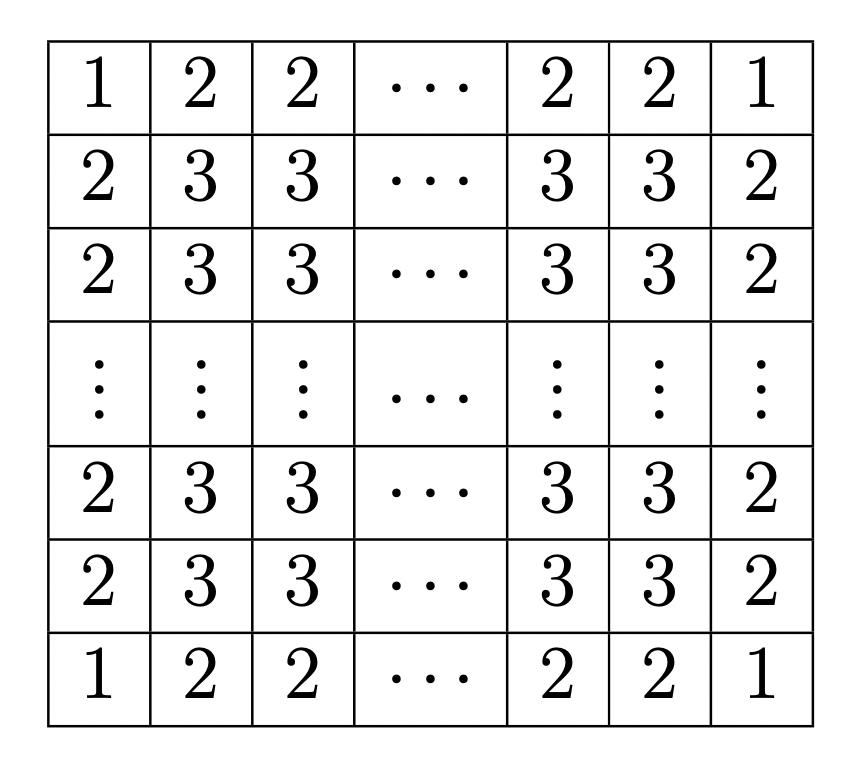
Ce nombre minimal est facile à exprimer : il doit y avoir autant de grains sur une case que le nombre de voisines moins un de cette case (si une case à 4 voisines, elle doit avoir au moins 3 grains de sable, etc.), comme on le représente sur la figure suivante.
Cet ensemble $G$ est appelé par les mathématiciens groupe abélien1 des tas de sable. Le tas nul $0_{\mathrm{TSS}}$ n’est pas dans $G$, mais pour l’addition des TSS, $G$ admet son propre élément neutre. Et vous savez quoi? Cet élément neutre n’est pas le tas nul, ni un tas constant… en fait, il est un peu difficile à expliciter celui-là (pour plus de détails, voir le chapitre 6 de Divisors and Sandpiles, de Scott Corry et David Perkinson2). Des images seront plus claires que les symboles mathématiques :
Dans les figures suivantes, voici des exemples d’éléments neutres pour l’addition du groupe abélien des tas de sable sur une grille de 16 carrés de côté et de 100 carrés de côté. Chaque couleur représente un nombre de grains de sable ($0$, $1$, $2$ ou $3$). Le bleu représente $0$ grains de sable, le jaune $1$, le noir $2$ et enfin le rose $3$. Les couleurs ont été choisies dans un but purement esthétique.
Et voilà un zéro bien original !