Un groupe $G$ est un ensemble muni d'une opération qui à deux éléments de $G$ associe un élément de $G$ (on appelle cela une loi de composition interne)1, laquelle doit vérifier (en notant cette opération $*$) :
- pour tout $x$, $y$ et $z$ dans $G$, $$(x*y)*z = x*(y*z) $$ on dit que l'opération est associative (c'est-à-dire que l'ordre dans lequel on effectue une série d'opérations n'importe pas) ;
- Il existe un élément $e$ qui, pour tout élément $x$ de $G$ vérifie $$ x *e =e *x =x $$ on appelle cet élément l'élément neutre ;
- pour tout élément $x$ de $G$, il existe un élément $y$ de $G$ vérifiant $$ x*y =y*x =e $$ $y$ est alors appelé l'inverse de $x$.
L'exemple le plus simple est sans doute l'ensemble des entiers relatifs $\mathbb{Z}$ muni de l'opération d'addition usuelle :
- en effet, on peut vérifier que $x+(y+z) = (x+ y)+ z $ ;
- l'élément neutre est bien sûr $0$ : pour tout $x$ de $\mathbb{Z}$, on a bien $x+0=0+x = x$
- et pour tout $x$ de $\mathbb{Z}$ il existe bien un inverse : par exemple pour $x = 2$, l'élément $y$ qui vérifie $2 + y = y + 2 = 0$, est, bien sûr, $y = -2$ (on comprend au passage pourquoi $\mathbb{N}$ ne peut être un groupe pour l'addition, car à part $0$, aucun autre élément n'admet un inverse appartenant à $\mathbb{N}$!)
On peut remarquer dans ce cas une certaine redondance dans les formulations du type $x+0=0+x = x$, ce qui est dû au fait que l'addition est commutative sur $\mathbb{Z}$ ; dans la définition, rien n'indique que l'opération $*$ est commutative (et, comme on le verra dans le dernier exemple ci-dessous, ce n'est pas toujours le cas!).
Historiquement, la notion de groupe a commencé à émerger sur des ensembles de permutations (par exemple si l'on regarde les permutations de trois éléments quelconques $a$, $b$, $c$, on obtient 6 permutations possibles qui, pour la composition, vérifient bien les axiomes de la définition). Ce point de vue à été en particulier utilisé par Galois pour démontrer l'époustouflant résultat de l'impossibilité de résolution par radicaux des équations de degré strictement supérieur à 4, après des siècles de tâtonnement sur d'hypothétiques formules de résolution.
On peut citer également une présence assez naturelle de cette notion en géométrie, lorsque l'on considère des isométries de l'espace ou du plan.
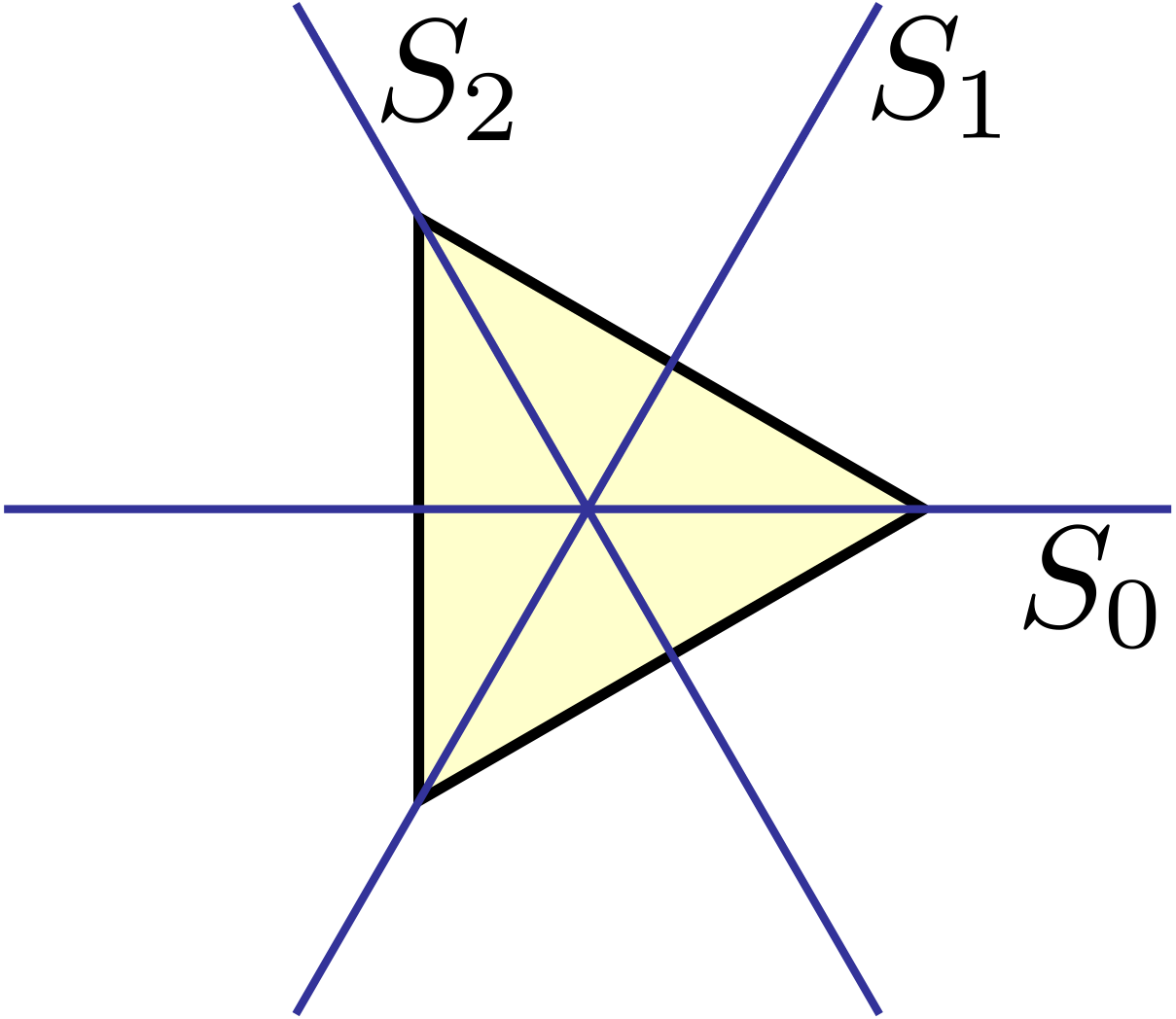
Donnons ainsi l'exemple du groupe diédral $D_3$ : le groupe des isométries qui laissent invariant un triangle équilatéral (il s'agit du plus petit groupe non abélien). En plus de l'identité, il y a deux rotations d'angles (dans le sens trigonométrique) respectivement $\frac{2\pi}{3}$ et $\frac{4\pi}{3}$, ainsi que trois symétries axiales dont voici les axes (fig. à droite) :
En notant multiplicativement la loi de composition, on a, par exemple, en notant $r_1$ la rotation d'angle $\frac{2\pi}{3}$, $r_2$ la rotation d'angle $\frac{4\pi}{3}$ et $Id$ l'identité, que $r_1\cdot r_2 = Id $ (comme on le voit facilement en donnant un nom à chaque sommet du triangle et en appliquant successivement les deux rotations).
Avec des considérations géométriques élémentaires, on est ainsi capable d'écrire la table de multiplication complète de ce groupe !
| $\cdot$ | $Id$ | $r_1$ | $r_2$ | $s_0$ | $s_1$ | $s_2$ |
|---|---|---|---|---|---|---|
| $Id$ | $Id$ | $r_1$ | $r_2$ | $s_0$ | $s_1$ | $s_2$ |
| $r_1$ | $r_1$ | $r_2$ | $Id$ | $s_1$ | $s_2$ | $s_0$ |
| $r_2$ | $r_2$ | $Id$ | $r_1$ | $s_2$ | $s_0$ | $s_1$ |
| $s_0$ | $s_0$ | $s_2$ | $s_1$ | $Id$ | $r_2$ | $r_1$ |
| $s_1$ | $s_1$ | $s_0$ | $s_2$ | $r_1$ | $Id$ | $r_2$ |
| $s_2$ | $s_2$ | $s_1$ | $s_0$ | $r_2$ | $r_1$ | $Id$ |