Mais quels sont les liens gorgés de sens que partagent ces deux théorèmes millénaires ?
Au lecteur
Avec cet article, les auteurs nous proposent des Travaux Pratiques autour (des théorèmes) de Thalès et de Pythagore. Dans l'inconscient collectif, ces deux noms bien connus des collégiens symbolisent presque à eux seuls la géométrie — du moins dans un cadre scolaire. Or, que peut-on dire du rapport entre les deux ? Dans le cas général, ils ne coexistent pas toujours : le théorème de Pythagore exige un produit scalaire, tandis que le théorème de Thalès se contente d'un espace affine1. L'intérêt est ici, dans le cas particulier du bon vieux plan euclidien, de les faire dialoguer, jusqu'à la résonance.
Matériel utilisé : règle, compas, équerre, rapporteur.
Notions abordées : angles correspondants, angles inscrits, arc capable, triangle isocèle, théorème de Thalès, théorème de Pythagore, cocyclicité, puissance d'un point par rapport à un cercle, symétrie, second degré.
Trônant au Panthéon des mathématiques, les théorèmes de Thalès1 2 et de Pythagore3 4 figurent en bonne place des programmes du collège progCollege. Leur influence s'étend jusqu'au lycée, voire au-delà dans notre quotidien. Ainsi, l'un éclaire la distributivité de la multiplication scalaire sur l'addition vectorielle, soit $\lambda\cdot(\bf u + \bf v)=\lambda\cdot \bf u+\lambda\cdot \bf v$, autant qu'il assure aux lignes trigonométriques une définition consistante, quand l'autre caractérise l'angle droit ou prélude à la relation si célèbre $\cos^2+\sin^2=1$. Ils se tiennent donc au service de la cartographie, de l'urbanisme, de l'architecture, de la mécanique, etc. Mieux, on le voit bien à ces exemples : dès que Thalès est quelque part, Pythagore n'est jamais très loin. Et vice-versa. Ce n'est pas surprenant car à en sous-main agit la notion d'aire. En quatrième, ne prouve-t-on pas Pythagore en assemblant les fragments d'un puzzle à quarrer ? Deledicq2000 En troisième, ne prouve-t-on pas Thalès en comparant deux « chevrons » — des surfaces profilées en ailette perrin2011mathematiques ? Fondées sur des axiomatiques différemment formulées ou différemment exploitées, d'autres approches existent, certainement 56789101112. Mais en agençant bien les ingrédients de la géométrie classique, il demeure toujours possible de se faufiler d'un théorème à l'autre.
L'aller Thalès-Pythagore est un classique qui aura figuré dans les manuels jusqu'aux années 1980 Louquet80. Le retour, Pythagore-Thalès, exigera plus efforts. À cet effet, nous passerons par le cercle — un détour qui unifie des résultats considérés comme fondamentaux mais souvent présentés séparément dans les curriculums. Enfin, pour souligner qu'il n'est nullement question de substituer un théorème à l'autre, nous traiterons un problème (aux multiples variantes), parfois nommé l'énigme des « échelles / ladders » Gardner96, où les rôles de l'un et de l'autre seront indispensables et également sollicités. L'ensemble pourra constituer la matière à des travaux pratiques en guise de révision du brevet, ou d'approfondissement.
proposition
Thalès vers PythagoreLes caractérisations connues sur les triangles semblables permettent d'établir le théorème de Pythagore.
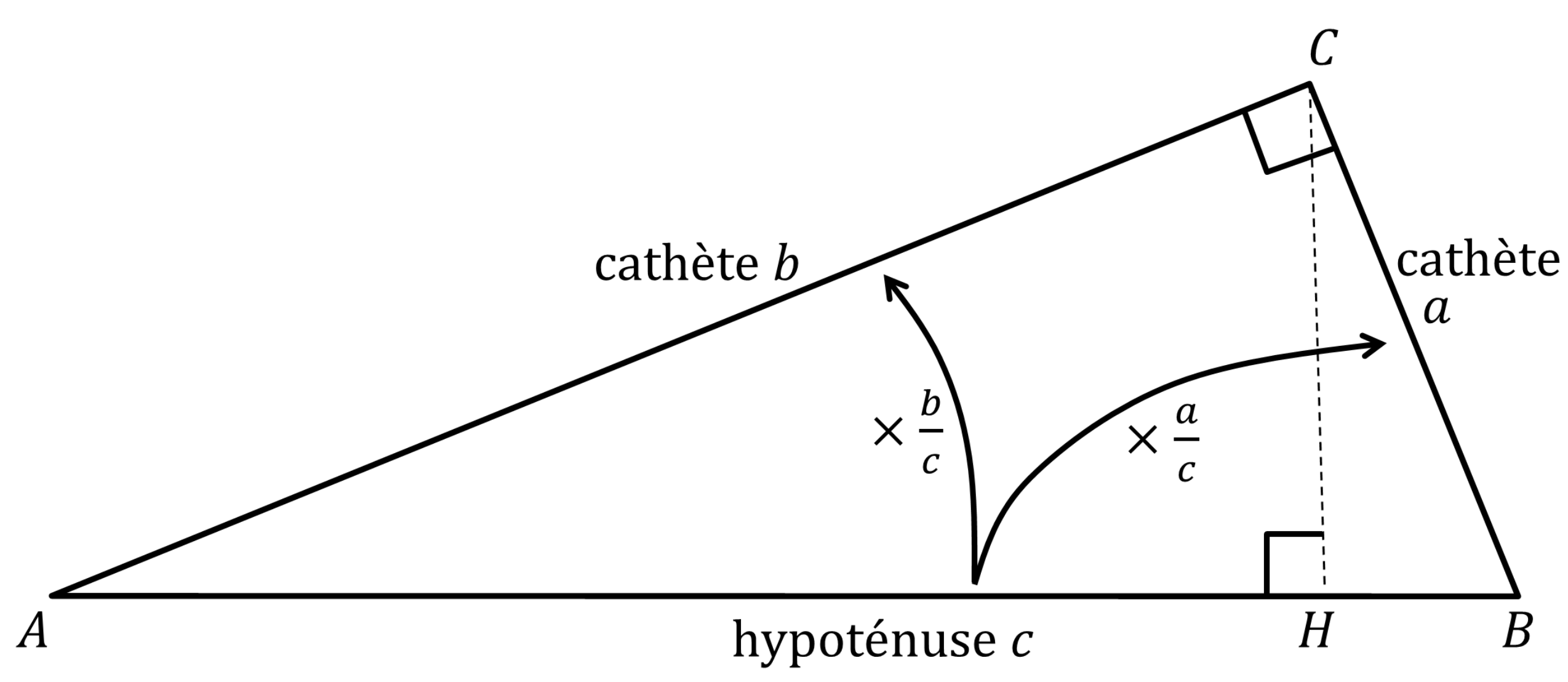
Preuve : En Figure 1, un triangle $ABC$ rectangle en $C$ est posé sur son hypoténuse1. Divisons ce triangle en menant la hauteur issue de $C$ jusqu’à son pied $H$ et partageons l'aire en deux : \begin{equation}\label{sommeAires} \mathcal{A}_{ABC} = \mathcal{A}_{CAH} + \mathcal{A}_{BCH} \end{equation}
Les triangles $CAH$ et $ABC$ ont chacun un angle droit. Ils ont aussi un secteur angulaire en commun, donc en complétant jusqu'à $\pi$, un troisième angle égal. Dès lors, ils sont semblables. Le coefficient de proportionnalité se retrouve dans le rapport des hypoténuses et intervient, au carré, dans le rapport des aires. Si bien que $\mathcal{A}_{CAH}=(\frac{AC}{AB})^{2} \mathcal{A}_{ABC}$. De même, $BCH \sim ABC$ puis $\mathcal{A}_{BCH}=(\frac{CB}{AB})^{2} \mathcal{A}_{ABC}$. En remplaçant dans la formule \eqref{sommeAires}, puis en simplifiant par $\mathcal{A}_{ABC}$ on retrouve bien \begin{equation} AB^{\;2} = AC^{\;2} + CB^{\;2}. \end{equation} ☐
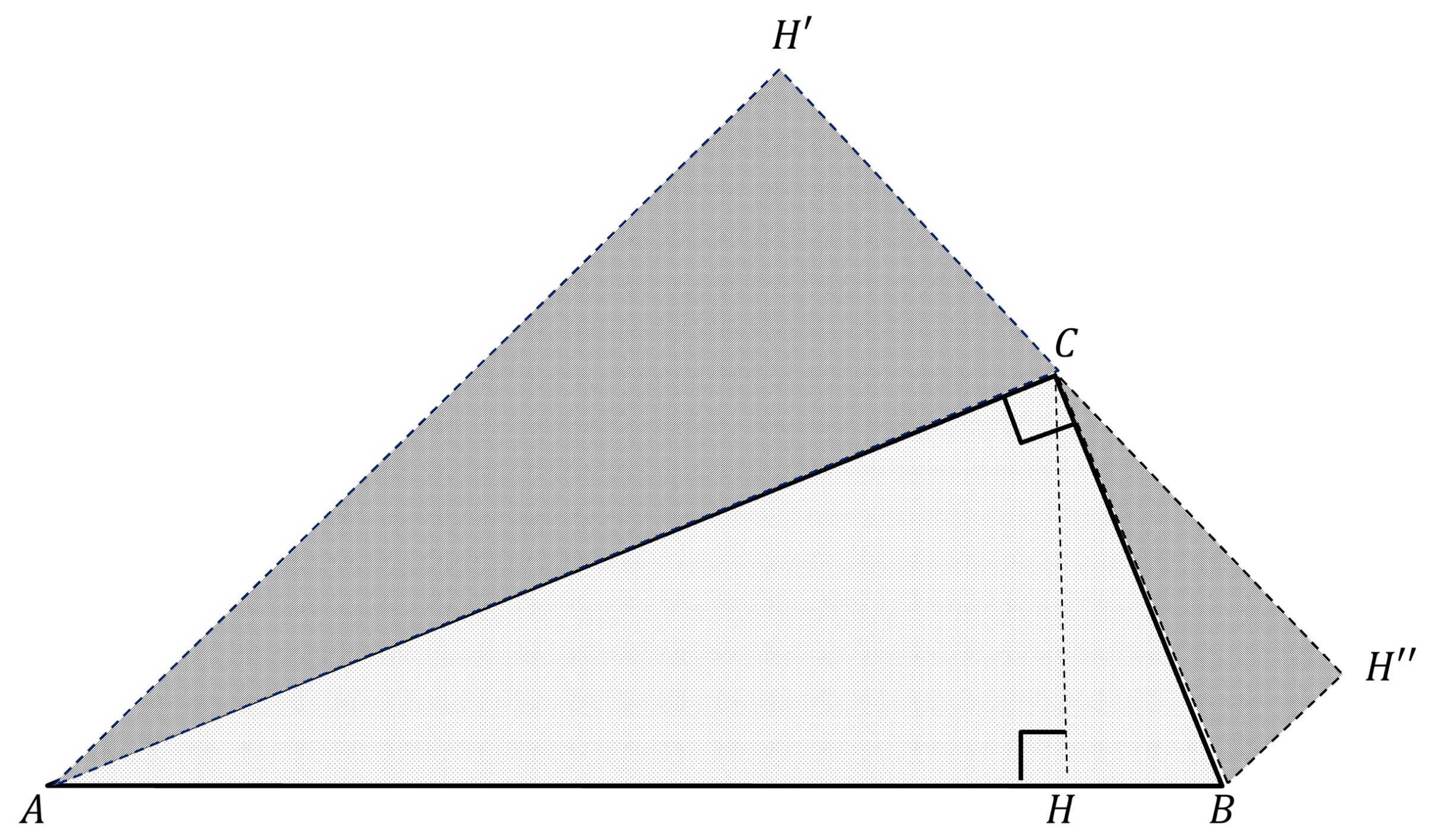
Dans cette preuve, l'utilisation de similitudes n'était pas si intuitive au premier regard. Nous devinons toutefois leur intérêt en symétrisant d'abord le point $H$ par rapport aux côtés adjacents : les ressemblances des triangles $ABC$, $ACH'$ et $CBH''$ sont alors frappantes, comme sur la Figure 2.
Proposition
Pythagore et la cocyclicité mènent à Thalès Le théorème de Pythagore, associé aux propriétés angulaires du cercle, permet de démontrer la proportionnalité de deux triangles emboîtés.
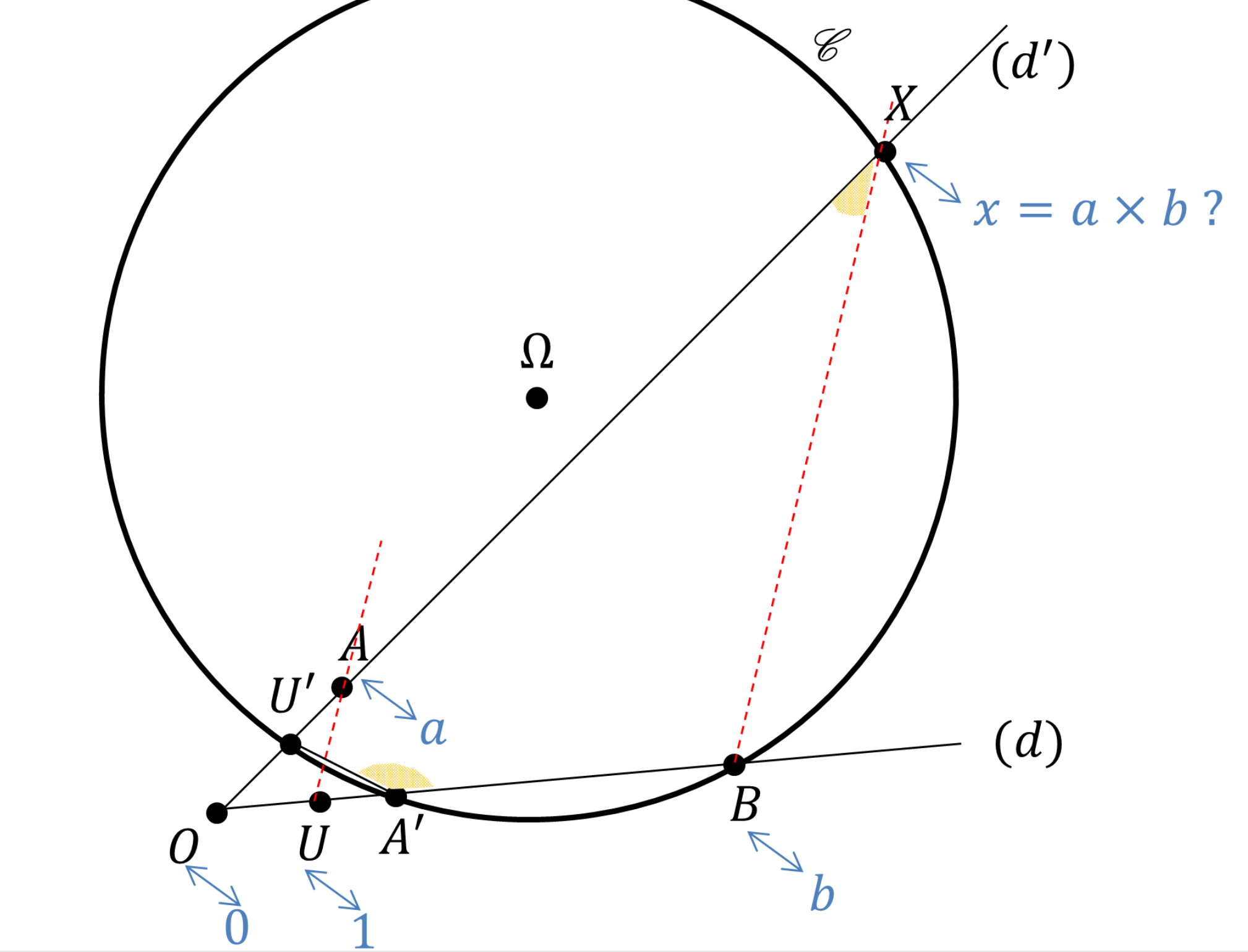
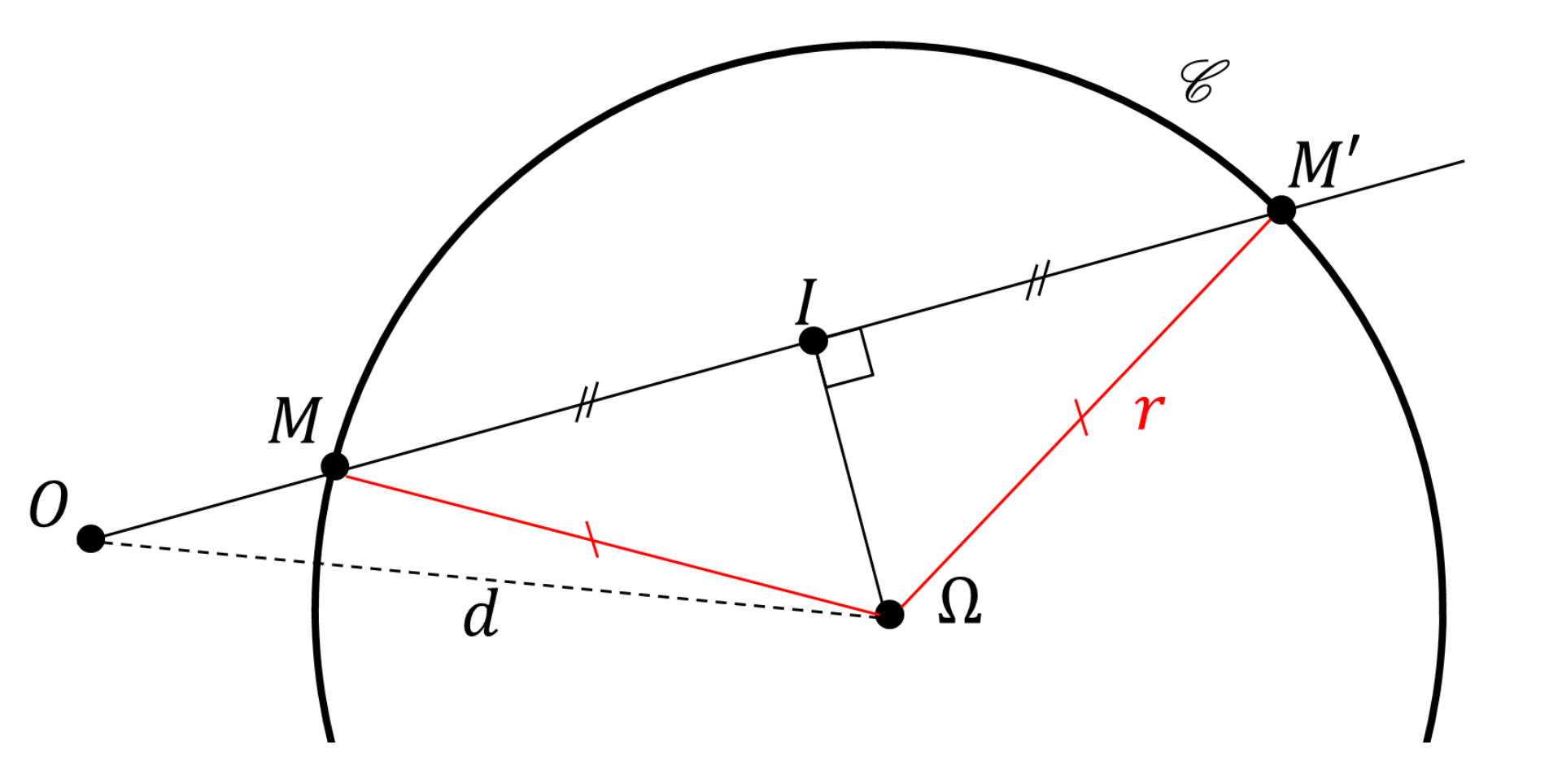
Preuve : Traçons deux axes $(d)$ et $(d')$ sécants en un point $O$, Figure 3. Disposons sur $(d)$ le point $U$ rattaché par principe à l'abscisse unité, et le point $B$ rattaché à l'abscisse $b$. Plaçons sur $(d')$ le point $A$ d'abscisse $a$. La parallèle à $(UA)$ passant par $B$ intersecte l'axe $(d)$ au point $X$. Il nous faut vérifier que son abscisse, $x$, vaut le produit $a\times b$ de $a$ et $b$. Par commodité, nous supposerons $1 \lt a \lt b $ afin d'alléger le croquis.
En miroir, marquons les points $U'$ d'abscisse 1 sur $(d)$ et $A'$ d'abscisse $a$ sur $(d')$. Par symétrie, $\widehat{U'A'U} = \widehat{U'AU}$. Or les angles $\widehat{U'AU}$ et $\widehat{U'XB}$ sont correspondants, donc égaux puisque $(UA) \parallel (BX)$. Si bien que $\widehat{BA'U'} = \pi - \widehat{U'XB}$. Les points $U'$, $A'$, $B$ et $X$ sont par conséquent cocycliques. La puissance du point $O$ par rapport au cercle $\mathcal{C}$ qui les relie impose $OU' \times OX = OA' \times OB$, soit $1\times x = a \times b$. D'où l'égalité entre les rapports \begin{equation} \frac{OB}{OU} = \frac{OX}{OA} \end{equation} ☐
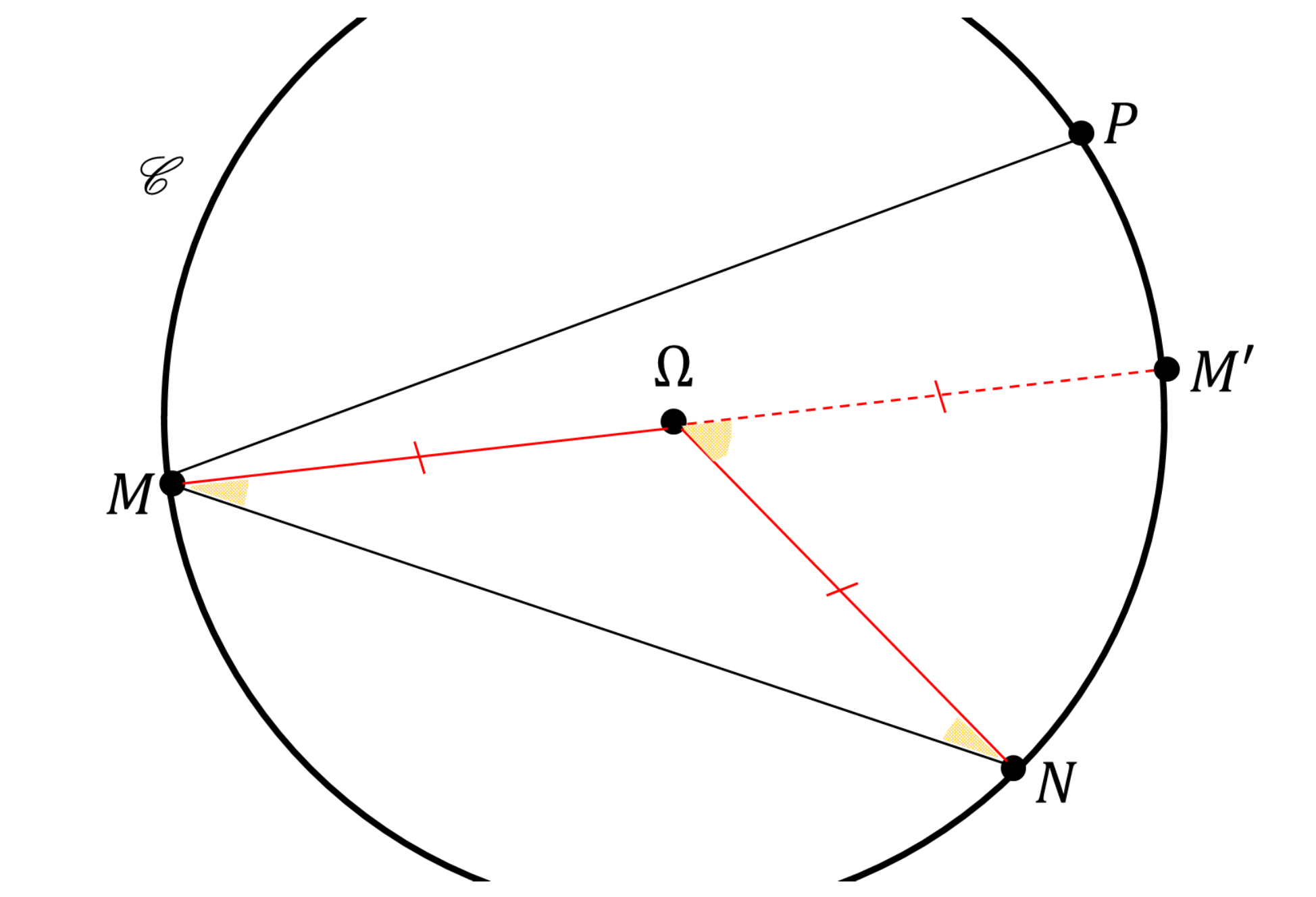
Diantre... où se cachait Pythagore ? Les premiers arguments cités, qui touchent aux égalités d'angles, remontent à Euclide Coxeter89, Stillwell05Stillwell05. La cocyclicité, que nous invoquons ensuite, est également un concept très primitif, découlant du pons asinorum comme le suggère la Figure 4. Enfin, la puissance d'un point par rapport à un cercle peut se déduire du théorème de... Pythagore, ce qu'atteste la Figure 5.
Les schémas ont été volontairement simplifiés. Il conviendrait d'« algébriser » les mesures. En effet, sur la Figure 3, les signes de $a$ et $b$ doivent pouvoir s'opposer, ce qui donne lieu à un graphique en papillon. En Figure 4, les trois points $M$, $N$, $P$ pourraient se trouver sous l'axe $(MM')$, ce qui oblige à retrancher des angles. En Figure 5, le point $O$ pourrait être intérieur au cercle, on orienterait donc l'axe $(MM')$. Toutefois, les grandes idées décrites ici ne changeraient pas significativement d'une configuration à l'autre.
Angles correspondants, angles inscrits, arc capable, symétries, similitudes, théorèmes de Thalès et de Pythagore, règle, équerre, compas : tout se tient dans ce condensé de géométrie euclidienne1, et il y a là quelque chose de déraisonnablement fascinant.
Voyons maintenant comment associer nos deux théorèmes.
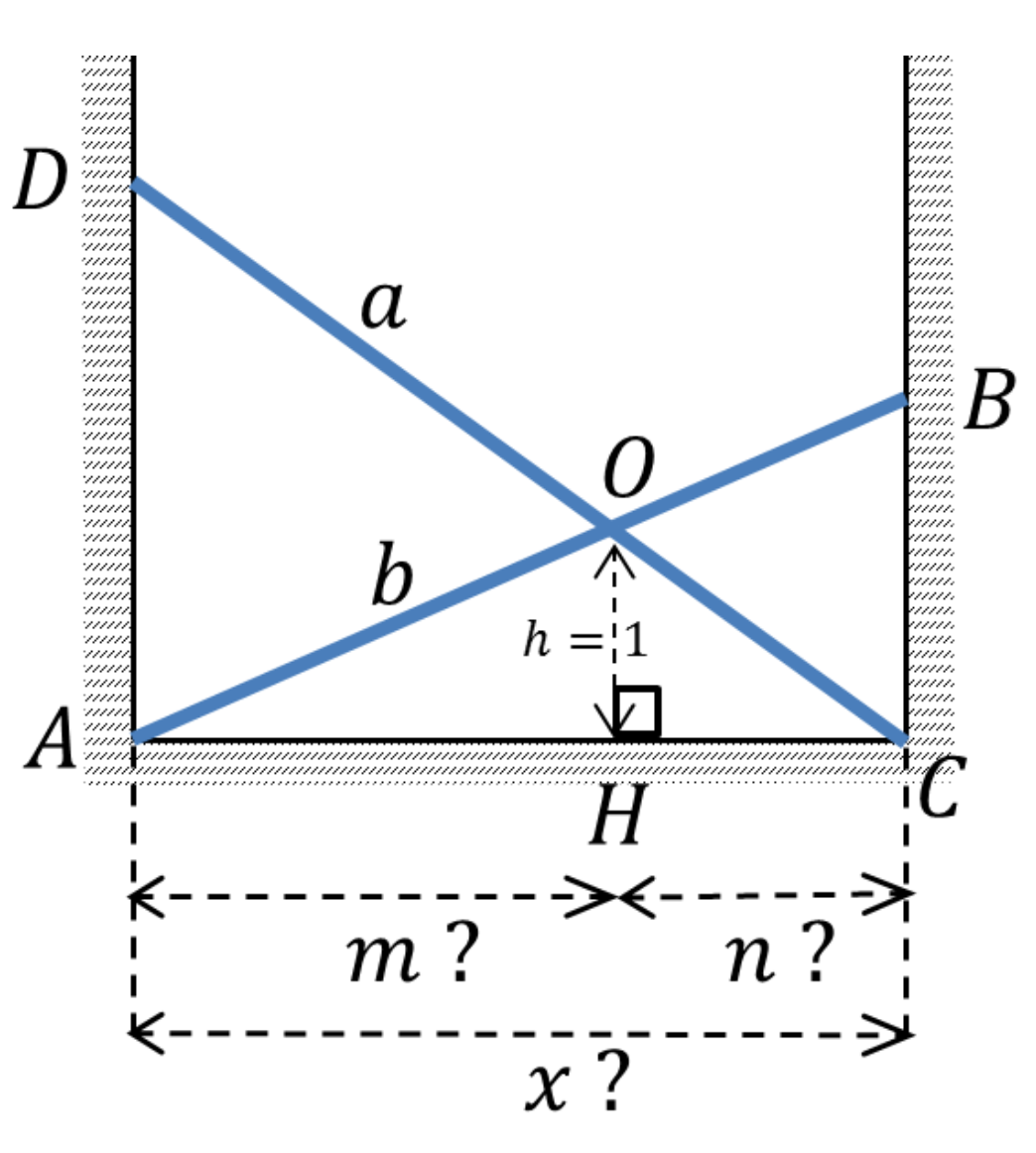
Fils d'Alcmène et de Zeus, héros de la mythologie grecque, doué d'une force surhumaine, Héraclès est parfois représenté à l'œuvre, déracinant deux imposants piliers (figurant deux montagnes) au cours d'un voyage dans l'Atlas (Maroc), Figure 6. Imaginons la suite. Les deux colonnes chancèlent, se croisent en $O$, puis se figent, adossées aux parois comme le modélise modélise la Figure 7. Témoin de la scène, le Sphynx questionne alors :
La hauteur $h=1$ de $O$ choisie comme unité, les longueurs $a$ et $b$ des colonnes connues, déterminer la largeur $d$ du temple. Héraclès, ce nouveau travail est pour toi.
Décomposons l'inconnue $x=AC$, en deux inconnues auxiliaires $m=AH$ et $n=HC$ de sorte que $m+n=x$. On a $a=AB$, $b=CD$. Puis laissons faire Thalès. Dans le triangle $ABC$, les droites $(OH)$ et $(BC)$ étant parallèles, \begin{equation} \frac{m}{x}=\frac{1}{BC}.\label{equation1} \end{equation} De même, dans le triangle $ACD$ \begin{equation} \frac{n}{x}=\frac{1}{AD}.\label{equation2} \end{equation} En ajoutant (\ref{equation1}) et (\ref{equation2}) nous obtenons \begin{equation} 1=\frac{m}{x}+\frac{n}{x}=\frac{1}{BC}+\frac{1}{AD}.\label{equation3} \end{equation} Autrement dit, $BC$ et $AD$ ont pour moyenne harmonique $2$. Au tour de Pythagore maintenant. Dans les triangles $ABC$ et $ACD$ rectangles, \begin{equation} x^2=b^2 - BC^2 = a^2 - AD^2 \label{equation4} \end{equation} Il nous faut combiner (\ref{equation3}) et (\ref{equation4}). Plusieurs stratégies se présentent à ce stade. Une première idée consiste à poser $u = AD$. Cependant, compte-tenu des quotients en lice dans \eqref{equation3} il semblerait judicieux de transiter par $u = \frac{1}{AD}$, et, mieux, dans un souci d'équilibre, par $u+\tfrac{1}{2} = \tfrac{1}{AD}$. En effet, quand $a=b$, on anticipe $BC=AD=2$, soit les valeurs $\tfrac{1}{BC}=\tfrac{1}{AD}=\tfrac{1}{2}$, à corriger à la hausse pour l'une et à la baisse pour l'autre, ou inversement, selon que $b\lt a$ ou non. Ceci conduit à \begin{equation*} b^2-\frac{1}{\Big(\frac{1}{2}-u\Big)^2}=a^2-\frac{1}{\Big(\frac{1}{2}+u\Big)^2} \end{equation*} puis à l'équation du quatrième degré (au plus) \begin{equation*} (a^2-b^2)\Big(\frac{1}{4}-u^2\Big)^2-\Big(\frac{1}{2}-u\Big)^2+\Big(\frac{1}{2}+u\Big)^2 = 0 \end{equation*} qui se résume à l'équation bicarrée \begin{equation} (a^2-b^2)u^4 + \Big(2 - \frac{a^2-b^2}{2}\Big)u^2+\frac{a^2-b^2}{16} = 0.\label{equation5} \end{equation} Comme de bien entendu, le cas particulier $a=b$ revient à $u=0$, $BC=AD=2$, et finalement $x=2$. Dans le cas général, l'équation se résout par radicaux. En découle une solution pour $x$.