Étant donné un ensemble $E$, on appelle distance sur $E$ une application de $E^2$ dans $\mathbb{R}^+$ telle que :
- $d(x,y)=0 \iff x=y$ (séparation) ;
- $d(x,y)=d(y,x)$ (symétrie) ;
- $d(x,y)+d(y,z)≥d(x,z)$ (inégalité du triangle).
Un espace muni d'une distance est dit métrique. La distance usuelle en géométrie plane et la différence absolue entre deux réels sont des distances.
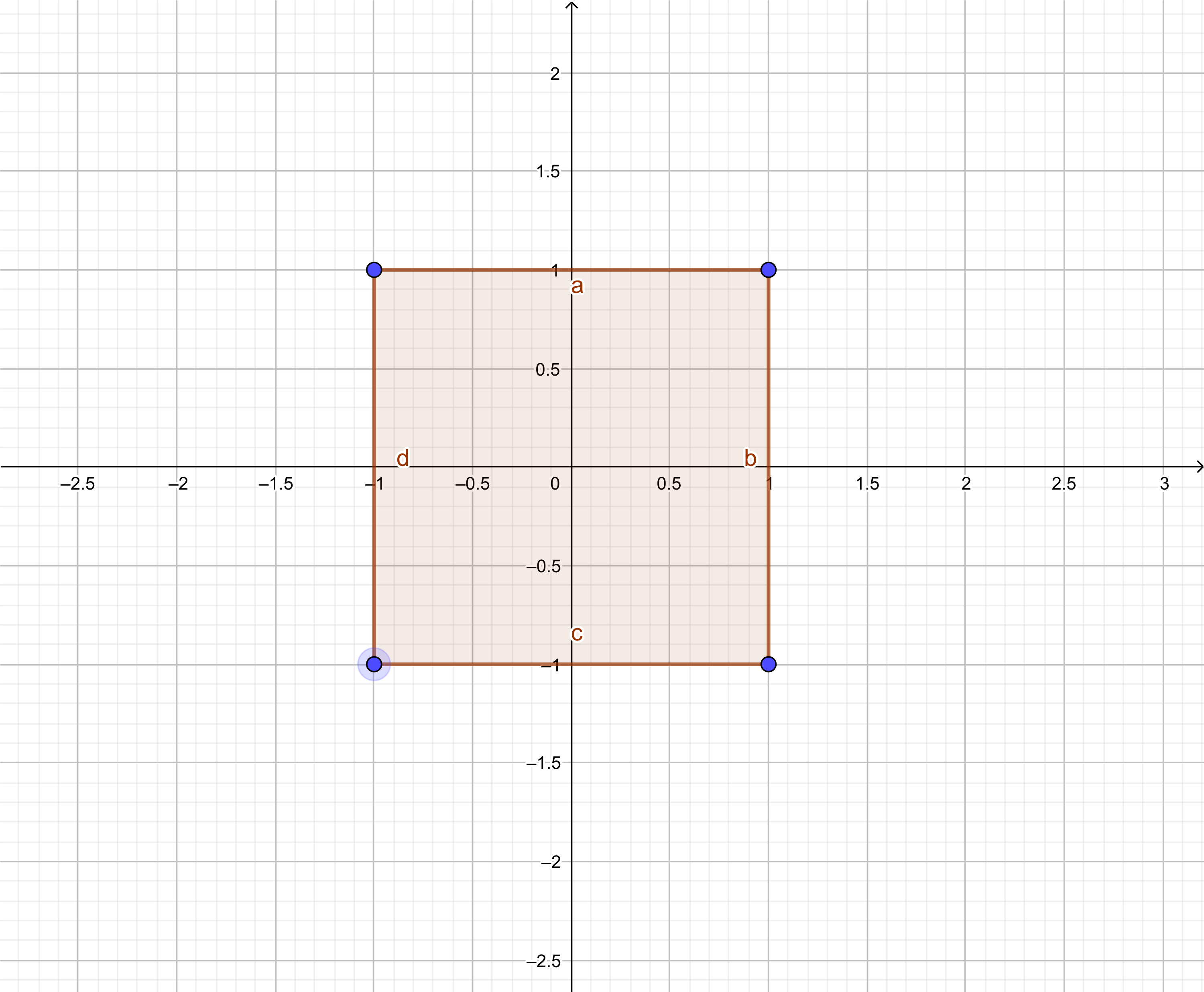
Certaines distances permettent de définir des boules carrées... Par exemple, dans le plan, définissons
$$d(A,B)=\sup(\mid x_B-x_A\mid ; \mid y_B-y_A\mid).$$
Alors, la boule centrée en l'origine et de rayon 1 (i. e. l'ensemble des points M tels que $d(O,M)≤1$) contient tous les points dont les deux coordonnées ont une valeur absolue inférieure à 1. Il s'agit de tous les points contenus dans un carré de côté 2, centré en $O$, et de côtés parallèles aux axes, comme l'illustre la figure ci-dessous.