S’intéresser à l’algèbre classique, à savoir l’algèbre des équations, c’est plonger dans l’histoire fascinante d’une discipline née entre 813 et 833, à Bagdad, à la cour du calife al-Ma’mūn. La question des sources de l’algèbre arabe n’est pas simple. Pour y répondre, l’historien des mathématiques doit se positionner au carrefour de plusieurs traditions. Parmi celles-ci, Ahmed Djebbar évoque les mathématiques babyloniennes, grecques et indiennes. La naissance de cette discipline avec ses objets propres (nombre, racine, bien), ses intentions, ses procédures est officielle avec le traité d’algèbre d’al-Khwārizmī où pour la première fois le mot « al-jabr » est utilisé comme opération mathématique. A partir de ce traité, de nombreux mathématiciens de langue arabe non seulement d’Orient, mais aussi d’Occident musulmans l’utilisent, le commentent et le prolongent. Leurs innovations concernent des chapitres aussi importants que la résolution des systèmes d’équations, la naissance et le développement des polynômes, le problème de la résolution des cubiques.

Ahmed Djebbar esquisse les grandes étapes de cette histoire dans cet entretien avec Marc Moyon. L'enregistrement est divisé en huit séquences indépendantes d'une dizaine de minutes, qui peuvent être regardées séparément ou enchaînées. Pour aller plus loin, on pourra se reporter à l'ouvrage « L'algèbre arabe. Genèse d'un art », qu'Ahmed Djebbar à publié en 2005, et au dossier d'accompagnement ci-dessous.

Annexes :

Sommaire des vidéos

1.  La transmission des traditions mathématiques anciennes aux savants de langue arabe : les héritages grec, indien, mésopotamien (17 min)
2. Al-Khwārizmī et ses intentions quant à son traité d’algèbre (12 min)
3. Le traité d’algèbre d'al-Khwārizmī : simple compilation des savoirs algébriques arabes ou traité novateurs ? (12 min)
4. Le développement de l’algèbre entre les 9° et 13° siècles : contemporains et successeurs d’al-Khwārizmī (7 min) 
5. Les systèmes d’équations : Abū Kāmil et al-Karajī (9 min) 
6. Les polynômes (11 min)
7. Les équations du troisième degré (10 min) 
8. L’Occident musulman (14 min)

Documents d'accompagnement

• Préface du livre "L'algèbre arabe, genèse d'un art", par Bernard Maitte
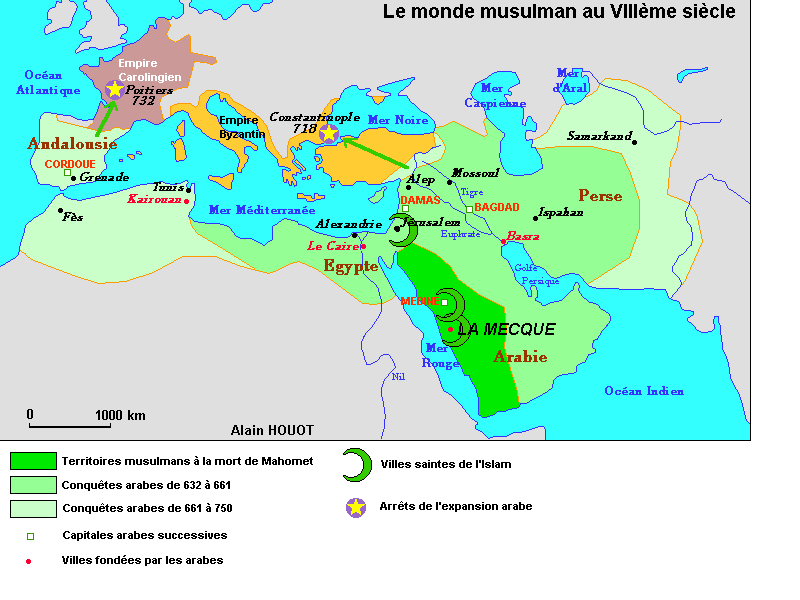
• Carte
• Index des noms propres cités dans les vidéos
• Bibliographie générale
• Publications d'Ahmed Djebbar
• Iconographie commentée et petits problèmes

Préface du livre « L'algèbre arabe, genèse d'un art »

C’est avec un grand plaisir que j’ai accepté d’écrire la préface de ce beau livre « L’Algèbre arabe, genèse d’un art ». L’auteur, Ahmed Djebbar, possède en effet des qualités rares. C’est un chercheur rigoureux, à qui l’on doit d’avoir retrouvé et porté à notre connaissance nombre de manuscrits mathématiques de l’Occident musulman et qui, en grand professeur, anime une équipe de docteurs et de doctorants qu’il lance en pionnier à la découverte de l’histoire des mathématiques, du Maghreb et de l’Espagne musulmane principalement.

C’est aussi — et tous ceux qui ont suivi ses cours ou assisté à ses conférences peuvent en témoigner — un merveilleux conteur qui, tel un griot, captive, passionne, donne l’intelligence d’un contexte, d’une perspective, d’une idée à des publics variés, qu’ils soient composés d’élèves du secondaire ou de chercheurs réunis dans un colloque.

Ahmed Djebbar œuvre ainsi pour la dignité de sa culture première et pour la reconnaissance de la place éminente qu’elle occupe dans le patrimoine de l’humanité. Loin des thuriféraires de la splendeur passée, des dogmatiques de tous poils, il se sert de l’histoire pour contribuer à éclairer le présent et veut que se renforce une citoyenneté nourrie d’humanisme et de la rencontre de l’autre. On le comprend, ce qui caractérise le plus l’auteur de ce livre, c’est la générosité radieuse et accueillante.

Le livre précisément. En le lisant, le non-spécialiste du sujet que je suis ressent une curieuse impression, un peu analogue à celle de quelqu’un qui découvre les ruines d’une ville jadis florissante. La perception est saisissante. Les restes épars témoignent de la grandeur des bâtisseurs, de leur génie. Chaque élément particulier participe à l’ensemble. Mais quel rôle jouaient ces débris ? Comment prenaient-ils place. Pour quelle signification ? Ayant découvert des restes, il faut les observer, les analyser, les restituer avant que d’espérer reconstruire la partie de la quelle ils se sont détachés, comprendre leurs fonctions, émettre des thèses quant à leurs relations, à leur contextualisation.

Les témoins dont nous parle « L’Algèbre arabe » sont des manuscrits, infiniment peu nombreux par rapport à une production qui a, d’évidence, été riche et importante. Ces reliques montrent d’abord et surtout l’ampleur de notre méconnaissance. Parmi les textes qui ont été exhumés, il y a plus de manuels que de références, plus de sources secondaires que d’œuvres originales. C’est la grande force d’ Ahmed Djebbar que de restituer ces fragments, de les montrer, de les désigner, d’en dégager le sens, plutôt que de se livrer trop hâtivement à une improbable reconstruction. Cette méthode rigoureuse montre les acquis, énonce les questions ouvertes, les recherches à effectuer si l’on veut progresser dans la connaissance de l’algèbre arabe. Cet art ne naît pas de rien : c’est la force de la civilisation arabo musulmane que de s’être appropriée et nourrie de pratiques, de techniques, de procédés, de traditions, d’idée préexistants dans les civilisations rencontrées lors de son expansion. C’est sa richesse d’avoir pu faire évoluer -oh combien- un art qui n’avait pas encore la dignité de la géométrie ou de la théorie des nombres. C’est sa spécificité que d’avoir permis à des auteurs s’exprimant en langue arabe, et d’origines et de confessions diverses, de contribuer à l’épanouissement des sciences. C’est sa caractéristique, dans une aire géopolitique allant de l’Inde aux Pyrénées, de posséder une grande unité culturelle et scientifique et de voir son Orient jouer un rôle moteur dans la maturation de l’algèbre, son Occident maghrébo-andalou un rôle prééminent dans une partie de son développement et sa circulation vers les pays latins.

Les pays latins s’approprient, diversement, l’art de l’algèbre à partir du XII^e siècle. Ils le poussent plus loin et ailleurs, lui donnent l’aspect que nous connaissons, celui d’une science. Cette phase d’appropriation et de dépassement se fait dans une filiation arabo musulmane assumée. Il faudra qu’au XV^e et XVI^e siècles des événements importants de la politique méditerranéenne (chute de Byzance, bataille de Lépante, …) interviennent pour qu’un regard nouveau soit porté par les latins sur le monde musulman. L’origine de l’algèbre sera alors gommée, ne restant présente que dans son nom. Aujourd’hui, ce regard n’est pas forcément renouvelé, ni chez le public occidental ni chez les sectateurs d’une grandeur passée magnifiée à l’excès.

On le comprend : ce petit livre est éclairant pour tous les hommes épris de culture, qu’ils soient ou non férus d’algèbre. Il est précieux aussi aux mathématiciens à qui il montre l’origine d’une partie de leur savoir. Il est indispensable aux chercheurs qui y trouveront les perspectives et les voies permettant d’orienter leurs investigations. Il pose enfin dans notre monde une question politique qui reste en filigrane. N’est-ce pas lorsqu’elles se constituent aux yeux de l’autre en s’appuyant sur la richesse de l’altérité que les civilisations prospèrent et s’épanouissent ? N’est-ce pas lorsqu’elles rejettent l’autre qu’elles régressent et se réifient ?

Bernard MAITTE,
Professeur d'Histoire de la Physique,
Université des Sciences et des Technologies de Lille

Carte